基于DEFORM的正挤结合侧挤大变形工艺研究

石凤健,王卫玲,熊成恺,肖汉青,李文进

(1.江苏科技大学 材料科学与工程学院,江苏 镇江 212003)(2.江苏科技大学 苏州理工学院,江苏 张家港 215600)

剧烈塑性变形通过累积大变形使材料内部产生足够大的应变来细化材料组织,所制备的材料组织致密,无孔洞.目前已提出的剧烈塑性变形技术包括等径角挤压、高压扭转、累积叠轧、往复挤压、多向锻造、搅拌摩擦加工、异步轧制等[1],其中针对等径角挤压的研究最为广泛[2-3].虽然等径角挤压能极大地细化材料的组织,提高材料的性能,但常规等径角挤压技术也存在一定的局限：一是工业化应用受到限制,要想获得具有大角度晶界的超细晶组织,所施加的等效应变往往要超过4,因此,需要多道次重复挤压才能满足获得超细晶所需的变形量；二是由于挤压过程往往不连续,重复装料以及挤出试样校正等导致加工效率低下;三是试样的长径比(或长宽比)不能过大,挤出坯料的长度受到限制,且挤压凸模易失稳,这些缺陷都严重影响了常规等径角挤压技术的工业化应用[4-5].

文献[6]提出了S型通道等径角挤压,该装置具有2个拐角,一道次挤压可累积更大的变形量.结合常规正挤压变形的优势,文中将正挤压与S型通道等径角挤压相结合,形成了新型的复合挤压工艺,其原理如图1.坯料先经过正挤压后进入S型通道进行等径角挤压,S型通道可以为一组或两组或者一组S型结合一组反S型通道的组合形式,实现不同的变形路线.该新工艺具有单道次变形量大、效率高等优点,具有一定的开发应用前景,但鉴于其模具结构的复杂性,文中采用DEFORM-2D软件[7-8]对该新工艺进行数值模拟,研究挤压过程中等效应变及载荷的演变过程,并与其它工艺进行对比,为进一步了解该工艺提供基础.

图1 正挤结合侧挤示意图Fig.1 Schematic illustration of forward extrusion integrated with lateral extrusion

1 模拟模型及参数

模拟采用刚塑性有限元进行,初始试样形状为长方形,正挤压和侧向挤压模具通道在垂直方向尺寸相同(图1),由于材料在该方向的变形很小,所以挤压过程可以简化为平面应变条件[7].模拟选用材料固溶态铜铬锆合金,其应力应变关系经测试后导入模拟软件.初始试样纵截面尺寸为40 mm×24 mm,挤压比λ为4,模具锥角α为150°,通道夹角Φ为105°,夹角外径R为2 mm,内径r为0.5 mm.摩擦模型选择剪切摩擦条件[9],摩擦系数取0.1.挤压在匀速条件下进行,速度为1 mm·s-1.挤压假定在室温下进行,且不考虑塑性变形热及摩擦热.

2 结果与分析

2.1 挤压变形过程

图2为试样在不同挤压阶段时的等效应变情况.可以看出,试样进行正挤压时,在模具锥角处由于通道横截面积收缩产生变形,但在这个区域的应变较小且试样的头部因为直接挤出几乎没有变形(图2a))；试样经过第1个夹角,发生剪切变形,其等效应变逐渐增大,但头部变形还是较小(图2b));试样经过第2个夹角,等效应变相比之前明显增大(图2c))；挤压结束时,除试样头部变形较小且不均匀外,在大部分区域等效应变沿试样长度方向的分布均匀一致,但在横向等效应变分布不是很均匀.中心区域等效应变较低,靠近试样次表面区域等效应变略高,呈近似对称分布(图2d)).

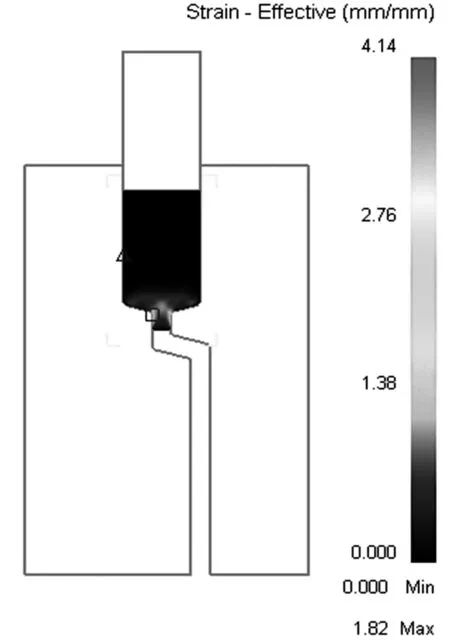
a)通过模具锥角

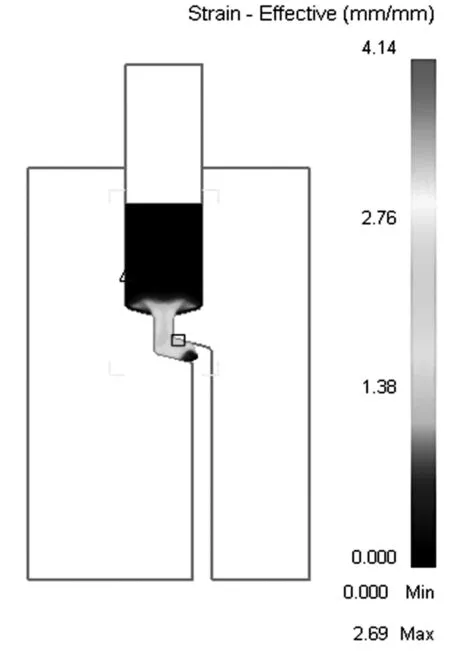
b)通过第1个夹角

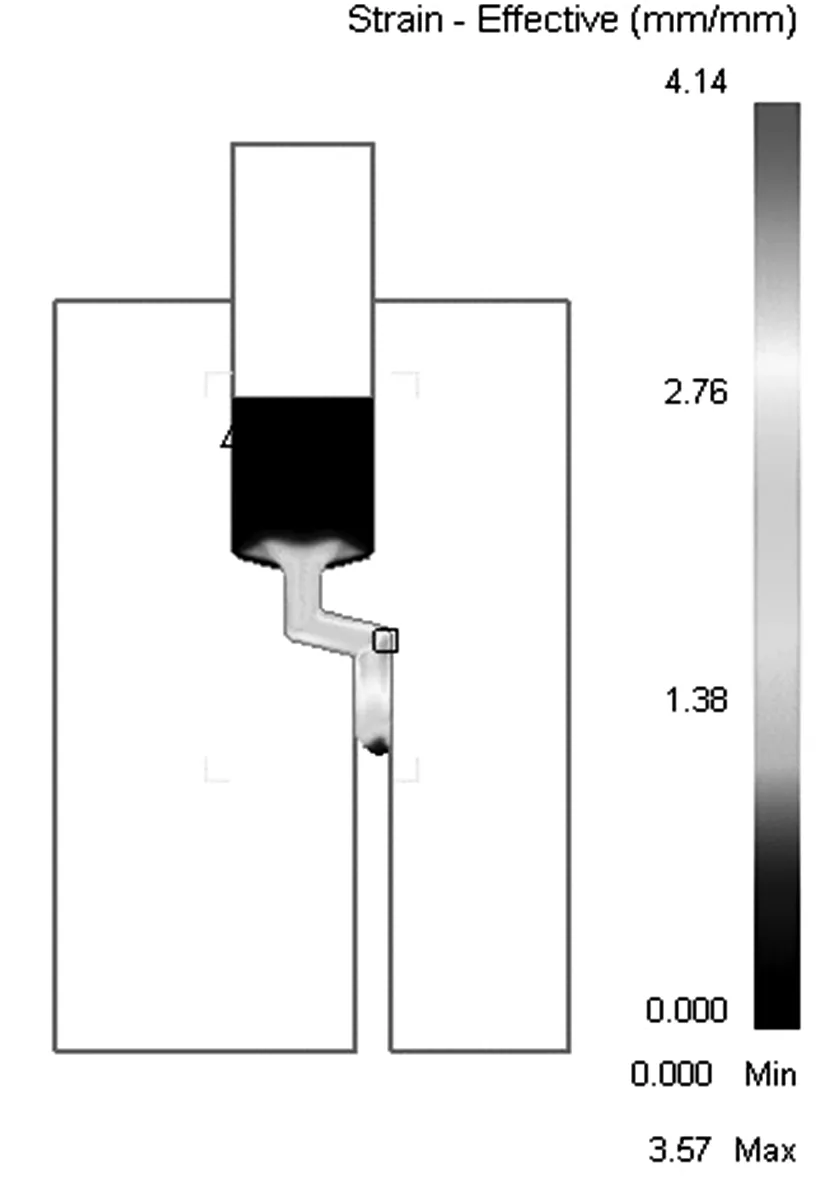
c)通过第2个夹角

d)挤压结束

图3为挤压载荷-行程曲线,曲线可分为3个阶段:第1阶段(A阶段)是正挤压阶段,挤压开始时挤压载荷为零,随着试样与模具锥角接触,试样开始发生塑性变形,挤压载荷急剧上升,之后进入稳态挤压阶段,载荷变得稳定;第2阶段(B阶段)是试样经过S型通道的第1个拐角,载荷在原正挤压的基础上进一步快速上升,当材料流过第1个拐角后逐渐地进入到一种稳定挤压阶段,载荷逐渐平稳;第3阶

段(C阶段)是试样经过S型通道的第2个拐角,载荷的变化过程与经过第1个拐角相似.

图3 挤压载荷-行程曲线Fig.3 Curve of extrusion load-stroke

2.2 挤压后的等效应变

为了能够定量地描述试样在挤压变形过程中等效应变的演变过程,取图4中的(1)P1-P2段、(2)P3-P4段和(3)P5-P6段,提取挤压后的等效应变,由图2d)可以看出,进入稳态挤压阶段后,在每个挤压阶段,等效应变沿试样挤出方向的等效应变较为一致,所以,图4取点线段位置具有代表性.图5为图4中P1-P2，P3-P4，P5-P6段的等效应变沿试样横向的分布,可以看出,试样经不同阶段挤压后等效应变总体不断增大,在3个位置处等效应变的分布相似,中间等效应变较低,靠试样次表面区域等效应变较大.值得注意的是经该新工艺一次挤压后平均等效应变可达约3.6,是常规等径角挤压后的3～4倍.根据文献研究结果,在该等效应变情况下,材料组织将发生明显细化,性能明显提高.此外,相对于正挤压部分和经过第1个拐角,经过第2个拐角后试样横向的等效应变分布更加均匀,这对于获得性能均匀的材料来说同样是非常重要的.说明经过正挤结合S型侧向挤压后,可以在材料内部产生足够高、且分布较为均匀的变形.

2.3 几种工艺方法的比较

图6为几种不同工艺挤压后的等效应变分布.图6a)为正挤结合S型侧挤模型:挤压比为4,通道夹角为120°,模具锥角为120°;图6b)为正挤模型:挤压比为4,模具锥角为120°;图6c)为S型侧挤模型,通道夹角为120°.图7为3种工艺挤压后横向的等效应变分布,可以看出,将正挤与侧向挤压相结合有利于获得更大且分布均匀的变形,对于高效制备大尺寸超细晶材料非常有利.

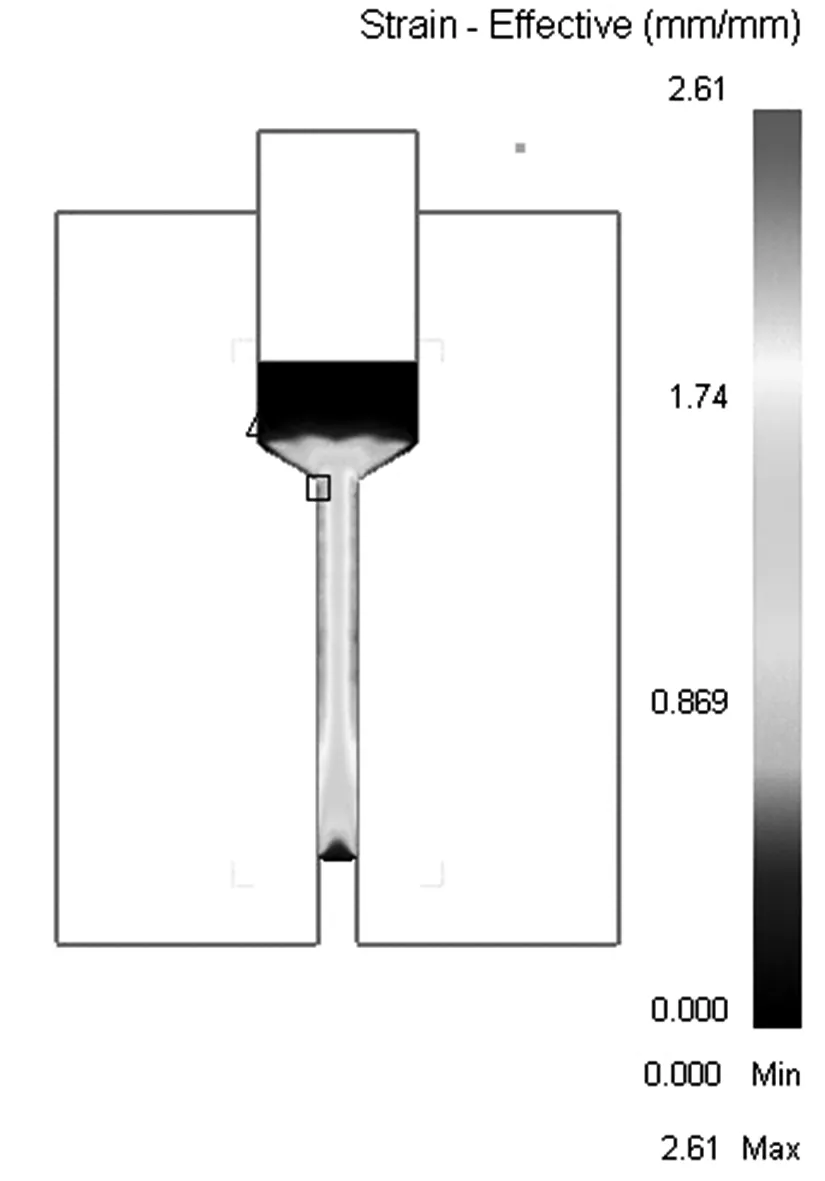
b) 正挤压

c) S型侧挤

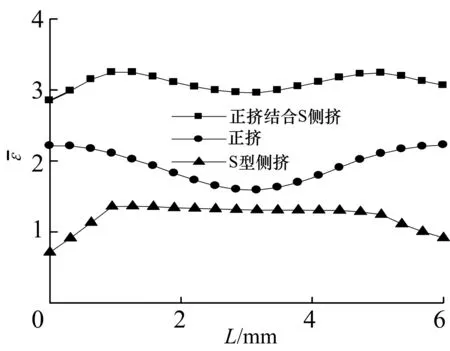
图7 不同工艺挤压后横向的等效应变分布Fig.7 Transverse effective strain distribution after extrusion by different processes

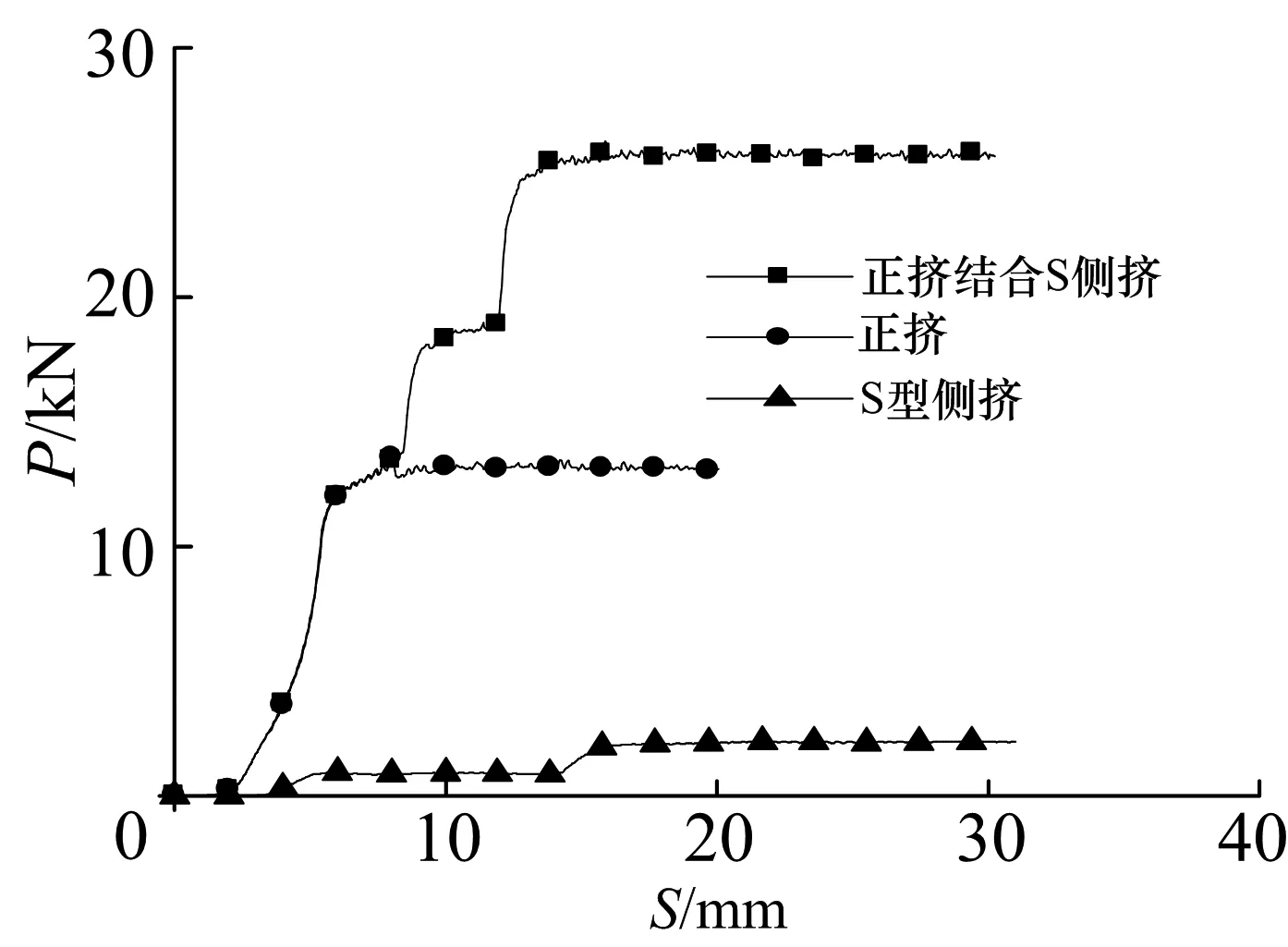
图8 不同工艺挤压时的载荷-行程曲线Fig.8 Load-stroke curve during different extrusion technologies

图8为3种工艺挤压时的载荷-行程曲线,可以看出,虽然正挤结合S型侧挤一道次变形量较大,但同时所需的载荷远远高于其它两种工艺,所以实际应用时,应针对挤压时的工艺参数进行优化,为模具设计及选材提供依据.

3 结论

文中针对正挤结合S型侧挤时材料变形过程、变形时的等效应变演变及与正挤压、S型侧挤压的对比进行了研究,得出了以下结论:

1)与常规等径角挤压工艺相比,材料经正挤结合S型侧挤一道次即可获得足够大的变形量,挤压效率明显提高,为解决常规等径角挤压工艺的工业化问题提供了途径;

2)正挤结合S型侧挤后等效应变更高且分布更为均匀,为制备性能均匀的超细晶材料提供了可能;

3)由于变形程度高,试样经正挤结合S型侧挤时所需载荷更大,所以应对挤压工艺参数进行优化,为该工艺的工业化应用提供保障.

[1] Wang Chengpeng,Li Fuguo,Chen Bo,et al.Severe plastic deformation techniques for bulk ultrafine-grained materials[J].RareMetalMaterialsandEngineering,2012,41(6): 0941-0946.

[2] Song M,Sun C,Jang J,et al.Microstructure refinement and strengthening mechanisms of a 12Cr ODS steel processed by equal channel angular extrusion[J].JournalofAlloysandCompounds,2013,577: 247-256.

[3] Bian M Z,Li Y L,Mathesh M,et al.Microstructure and texture evolutions and mechanical properties in pure copper by equal-channel angular pressing[J].JournalofAlloysandCompounds,2013,578: 369-372.

[4] Xu Cheng,Schroeder S,Berbon P B,et al.Principles of ECAP-Conform as a continuous process for achieving grain refinement:application to an aluminum alloy [J].ActaMaterialia,2010,58(4): 1379-1386.

[5] Chen Qiang,Zhao Zhixiang,Shu Dayu,et al.Microstructure and mechanical properties of AZ91D magnesium alloy prepared by compound extrusion [J].MaterialsScienceandEngineeringA,2011,528: 3930-3934.

[6] Liu Z Y,Liang G X,Wang E D,et al.The effect of cumulative large plastic strain on the structure and properties of a Cu-Zn alloy [J].MaterialsScienceandEngineeringA,1998,242(1-2): 137-140.

[7] Yoon S C,Jeong H G,Lee S,et al.Analysis of plastic deformation behavior during back pressure equal channel angular pressing by the finite element method[J].ComputationalMaterialsScience,2013,77: 202-207.

[8] 石凤健,郑富龙,邹妮康.模具外侧圆角对缩径侧向挤压变形影响的有限元分析[J].江苏科技大学学报:自然科学版,2012,26(4):346-349.

Shi Fengjian,Zheng Fulong,Zou Nikang.Finite element analysis of the effect of die outer corner on billet deformation during stretching lateral extrusion[J].JournalofJiangsuUniversityofScienceandTechnology:NaturalScienceEdition,2012,26(4): 346-349.(in Chinese)

[9] Balasundar I,Raghu T.Effect of friction model in numerical analysis of equal channel angular pressing process[J].Materials&Design,2010,31(1): 449-457.