切比雪夫不等式及其应用

何志华

(成都大学，四川 成都 610106)

大数定律，即随机事件的大量重复出现中呈现的一种必然趋势规律。后来泊松在其基础上提出了新的陈述和理论。通俗地说，这个定理是在恒定实验条件下，大量试验，随机事件的频率与概率几乎相同。

切比雪夫大数定律三条定理之一可描述为：当N个数量的期望值及其各自平方的期望值不超过给定值的值时，此N个量的算术平均数和数学期望值的算术平均值之差不小于给定概率，当N趋于无穷大时，其值趋于1。用现在的符号表达且比雪夫大数定律，有：设X1，X2，…，Xn，…是相互独立的随机变量序列，数学期望E(Xi)和方差D(Xi)同时存在(i=1，2，…)，且D(Xi)0，有：

一、切比雪夫不等式

上述定理需利用切比雪夫不等式来推导，假设X1，X2，…，Xn，…是相互独立的且不相关的随机变量序列，并且都存在方差，则对于任何ε>0，有：

可以看出这就是切比雪夫不等式。

二、切比雪夫不等式的应用

1.大数定律的推导依据。作为概率论极限理论的研究基础，切比雪夫大数定律和切比雪夫不等式的地位是众所周知的。首先，利用切比雪夫不等式推导出切比雪夫大数定律，可以说切比雪夫不等式也是其他大数定律的理论研究依据和关键手段，后续数学家们的研究将切比雪夫的研究推向更高地位。

2.在生活中概率事件的应用。关于切比雪夫不等式的应用，目前没有合理的摘要。任何一个随机变量，几乎所有的值都是将接近“平均”。在概率论中,切比雪夫不等式是对事件的上下界的估计。切比雪夫不等式的有限形式多用于代数中。例如在积分形式和微分形式中，可用于解决困难的积分不等式情况。其推广式在概率论中的应用、在生活中的小概率事件中的应用也较为广泛。且切比雪夫多项式一直是研究热点，其良好的特性，如正交性、奇偶性、有界性、完备性。对其应用产生的恒等式，得到一些积和式，对其推导也有新的递推式，其中切比雪夫多项式在各项研究应用广泛。

3.利用切比雪夫多项式可构造一系列切比雪夫矩阵,切比雪夫-范德蒙矩阵(切-范矩阵)的相关矩阵(广义切-范矩阵),等差型切比雪夫矩阵；可用来研究一元切-范导数矩阵、二元切-范偏导数矩阵、跨行切-范矩阵这三类广义切-范矩阵与范德蒙矩阵及广义切比雪夫多项式。国内外众多学者应用切比雪夫谱方法研究数值分析等应用。

首先，引入Markov不等式的介绍：假设XX是一个不小于0的随机变量，则：P(X>a)≤E(X)aP(X>a)≤E(X)a

此不等式仅仅通过使用随机变量的期望E(X)就给出了分布的概率范围，但是显然，该不等式被过度放大了，并不能提供正确的信息。进一步证明，就能够得到切比雪夫不等式

切比雪夫定理推论：X1，X2，…，Xn，…是相互独立的随机变量序列，数学期望E(Xi)=μ和方差D(Xi)=σ2(i=1，2，…)，则对任意给定的ε>0，有

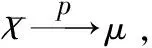
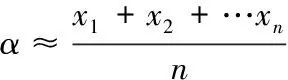
上式表明，当n足够大时，把n次测量结果的算术平均值作为a的近似值，所产生的误差是十分小的，具有一定的实际意义。

对于服从参数为p的0-1分布的随机变量X1，X2，…，Xn，…，显然DX(i)=p(1-p)<0.25(i=1,2,3,4,……),它符合服从切比雪夫大数定律的条件。

三、总结

综上，经过学者的研究，大数定律体系的发展已经很完备，也出现了更广泛的大数定律，生活中大多数概率事件都与大数定律、切比雪夫不等式相关，其应用于社会和工业生产，为人类的研究奠基。

[1]徐凤林.Chebyshev不等式的应用[J].北京石油化工学院学报,2011,10(3):10-12.

[2]甘大旺.切比雪夫不等式及两个推论[J].数字通讯,2016,12(2):59-61.

[3]林正炎，白志东.概率不等式[M].北京：科学出版社,2001.