基于正交设计与BP-GA算法的船体结构耐撞性能优化设计

张延昌,葛珅玮,刘 昆,胡宗文

(江苏科技大学 船舶与海洋工程学院,江苏 镇江 212003)

船舶碰撞引起的后果往往是灾难性的[1].开展船体结构耐撞性能优化设计的主要目的是在船舶碰撞研究的基础上对结构进行优化设计,提高船舶的耐撞性能,增加结构的安全性,降低损失.目前,国内有关结构耐撞性优化的研究主要集中在汽车领域,而船舶领域的研究较少.由于船体结构的复杂性给耐撞性优化设计带来了一定的困难,一些传统的优化方法已经不能满足要求了.

遗传算法(genetic algorithm,GA)是一种高度并行,随机搜索的优化算法,具有全局寻优能力,采用GA能取得很好的优化结果.但在结构分析中,目标函数与设计变量之间的隐式关系需要用有限元计算才能获得,而庞大的种群和遗传代数使得遗传操作效率低下,甚至难以进行.如果能得到变量与目标之间的映射关系,那么就可充分发挥遗传算法的优势.

近些年,人们已经利用响应面模型来模拟结构变量与目标之间的关系,以代替结构分析中的有限元计算,解决了优化低效的问题.人工神经网络是模拟大脑处理信息的一种数学模型,文献[2]中在Kolmogorov函数表示定理的基础上,证明了任意函数都能通过一个3层神经网络建立映射关系,这为神经网络响应面在结构优化分析中的应用提供了理论基础.BP网络是目前应用最广的神经网络,通过构造BP神经网络响应面模型能够实现结构的近似分析,提高优化效率.

正交试验设计简称正交设计,是根据统计学原理来安排多因素试验的一种科学方法[3-4],由正交试验设计的训练样本具有均衡分散性和整齐可比性.因此,用正交试验构造神经网络响应面的训练样本,不仅可以提高学习训练效率,还能够保证网络的泛化能力[5].

因此,基于正交试验设计、BP网络和遗传算法形成的耐撞性优化设计方法利用正交设计构造神经网络训练样本,建立BP神经网络响应面模型,结合遗传算法,能处理大型结构工程优化问题.

1 耐撞性优化设计方法

文中优化方法的基本思路:首先建立船体结构耐撞性优化设计数学模型;其次,利用正交试验设计合理的船体结构碰撞有限元仿真试验样本;然后训练这些样本,构造碰撞模型目标的BP神经网络响应面模型;最后将该模型结合遗传算法对目标进行优化.这种优化方法称作BP-GA算法,该算法的优化速度很快[6],具体操作流程如图1.

图1 BP-GA优化算法流程Fig.1 Flow chart of BP-GA

优化分析时,需要将实际问题进行抽象处理,形成优化问题的数学模型.实际船体结构耐撞性能优化研究是一项相当复杂的工作,舰船耐撞性优化数学模型的建立至关重要,而耐撞性优化目标函数将是耐撞性优化的关键所在.

1.1 耐撞性优化数学模型

对任何船体结构优化设计问题的数学模型可归纳如下:

(1)

式中:X为设计变量;f(X)为目标函数;gj(X)为不等式约束;lk(X)为等式约束.

船舶发生碰撞后,结构吸收碰撞动能的大小在一定程度上能够表征抵抗碰撞能力优劣.因此,在某一极限状态(如外板破裂、内壳破裂等)下,单位质量结构吸收的能量大小反映了结构耐撞性能,其表达式如下[7]:

βE=E/W

(2)

式中:E为结构的吸能,单位kJ;W为优化区域结构的重量,单位kg.

对于船舶结构来说,结构的塑性变形或破裂尺寸在一定程度上反映了结构的性能优劣.因此,在某一极限状态下,单位质量结构的变形或者破裂尺寸能反映结构的耐撞性能,其定义如下:

βc=D/W

(3)

式中:D为结构最大的塑性位移或破坏尺寸,单位mm;W为优化区域结构的重量,单位kg.

式(2)和(3)都反映了结构耐撞性能的优劣.因此,综合以上两式,文中提出了一种综合性的耐撞性优化指标如下:

(4)

式中:αE和αC分别为单位质量吸能、变形隶属度权重系数;f()函数为指标的隶属度函数(无因次量),隶属度计算方法如下:

(5)

式(4)能综合反映结构耐撞性能的优劣,该值越大,结构的耐撞性能越好，因为该值越大,就要求βE越大、βC值越小,即结构单位质量的吸能越大、变形越小,结构的耐撞性能就越好,这就能充分表示结构耐撞性能的优劣.文中将该综合指标作为船体结构耐撞性能优化分析时的目标函数.

1.2 正交试验设计

神经网络响应面的精度与其泛化能力紧密相关,一般通过对一组样本进行训练和学习来记忆样本输入和输出之间的关系.因此,训练样本集对于神经网络来说非常重要.若样本量过少,则样本不能反映输入和输出之间的内在规律关系,泛化能力不强,预报精度不高;若样本量过多,则在网络学习时将花去大量的时间,记忆过多的细节,使得网络结构过于复杂,而无法建立正确的响应面模型.

理论上已经证明了正交试验的均衡分散性会使得试验组合明显合理化[8],且能保证样本的典型性.由正交表安排的训练样本,不失一般性而又保证一定数量,避免了样本数量过少或者过大产生的问题,减少网络学习样本训练的时间,提高效率,进而也保证了神经网络响应面模型的泛化能力.

1.3 BP神经网络响应面模型

BP网络是目前应用最广泛的神经网络,体现了人工神经网络的精华.它属于多层前馈网络,包括输入层、隐含层、输出层,同层之间互不相连.BP算法在正向传播时,样本从输入层经隐含层传向输出层,若在输出层得不到期望值,则转向反向传播阶段,利用输出后的误差来估算前一层的误差,如此一层层的反传下去,通过调整神经元的权值,使得误差最小.这就形成了将输出层表现的误差沿着与输入相反的方向逐级向网络的输入层传递的过程.BP网络可以看成是一个从输入到输出的任意非线性映射.如果输入节点个数为m,输出节点个数为L,网络是从Rm→RL的映射,即

F:Rm→RL,Y=F(X)

(6)

式中:X,Y分别是样本输入和输出集合.

实验表明,在3层网络结构中,当m个输入神经元与n个隐层神经元大致存在m=2n+1关系时,网络响应面精度最佳[9],文中BP网络响应面模型的输入与输出神经元个数存在这样的近似关系.

1.4 遗传算法与罚函数

遗传算法通常把问题的求解描述成一个群体的进化过程,把问题的解表示成染色体,并基于适应度函数值按适者生存的原则来选择染色体,通过模仿生物的交配与变异过程,产生更适应环境的新一代体群,不断进化,直到产生最适合环境的种群.由于遗传算法独特的工作原理,使其具有很多传统优化方法无法比拟的优点.

针对标准遗传算法在实际操作中遇到的“早熟现象”问题[10],文中对选择、交叉、变异三种操作方式作了一定的改进.采用保留最优轮盘赌选择方式、自适应交叉与变异算子,其中,自适应交叉概率Pc和变异概率Pm的计算公式[1]如下:

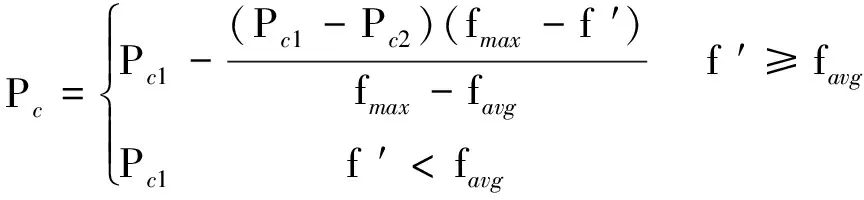
(7)

Pm=

(8)

式中:Pc1=0.9,Pc2=0.6,Pm1=0.1,Pm2=0.001

遗传算法只能直接处理无约束的优化问题,因此,必须对约束条件作一定的处理,通过罚函数[11-12]的方法将有约束问题转化为无约束问题,使遗传算法得以进行.罚函数对适应度函数的调整定义为

(9)

式中:F(X)为原适应度函数;F′(X)为添加罚函数后的新适应度函数;P(X)为罚函数;α为惩罚因子.

2 舷侧结构耐撞性优化设计

2.1 问题描述

利用前文优化方法对某船舷侧结构进行耐撞性优化设计.选取典型碰撞工况:撞击船艏部撞击被撞船中部,两船相撞时的航向夹角为15°,撞击船航速为16 kn,被撞船航速为14 kn.碰撞接触区域在货舱上甲板与下甲板间的舷侧结构,该区域为横骨架式,由舷侧外板、T-型肋骨、肘板及纵骨组成,主要受力构件为肋骨和舷侧外板,因此针对肋骨和外板进行优化.该结构原始设计尺寸如图2.

图2 碰撞区域结构尺寸Fig.2 Structural shape of collision region

图中,单个肋距为1.600 m,外板为24 m×2.64 m×0.015 m,T-型肋骨为⊥0.36 m×0.01 m/0.18 m×0.012 m.该区域材料均为DH32高强钢,屈服极限σy=3.15×108Pa,弹性模量σy=2.1×1011Pa,密度ρ=7 850 kg/m3.

有限元数值模型如图3;材料为Cowper-Symonds模型,D=40.4,q=5;碰撞接触区域采用较细网格,其余部分采用较粗网格;接触区域采用自适应主-从接触及自适应自接触.

a) 整体有限元模型

b) 碰撞区域板架有限元模型

在满足结构强度的同时考虑到制造工艺问题,确定设计变量.外板板厚tf在13.0～16.0 mm之间;T-型肋骨腹板厚度tc在8.0～11.0 mm之间;T-型肋骨腹板高度h在320～380 mm之间.其中tf,tc满足是0.5 mm的整数倍,h为整数.由于重量对船舶性能和建造成本影响很大,因此,将重量作为优化分析的约束条件,取m≤13 500 kg.总结设计变量、约束条件、目标函数,建立了如下船体结构耐撞性能优化的数学模型:

maxF=αE·f(βE)+αC·f(1/βC)

s.t. 13.0 mm≤tf≤16.0 mm

8.0 mm≤tc≤11.0 mm

320 mm≤h≤380 mm

m≤13 500 kg

式中:f()函数为目标隶属度函数,按式(5)计算;αE和αC分别为单位质量吸能、变形隶属度前权重系数.考虑到吸能与变形的同等重要性,取αE=0.5;结构碰撞区域未发生破口时取αC=0.5,发生破口时,取αC=0.05.

2.2 正交试验设计与直观分析

针对该优化问题的数学模型,考虑现有正交表模板以及船体结构的制造工艺,确定碰撞区域板架待优化主要构件各参数有4个水平,选用正交表L16(45)(空白两列),其外板厚度tf、肋骨腹板厚度tc、肋骨腹板高度h分别取以下离散值:外板厚度tf为13.0,14.0,15.0,16.0 mm;肋骨腹板厚度tc为8.0,9.0,10.0,11.0 mm;肋骨腹板高度h为320,340,360,380 mm.有限元试验安排及数据处理如表1.

直观分析[13](极差分析)是根据试验结果的极差大小来确定因素影响作用主次顺序的一种分析方法,极差越大,该因素对目标的影响越重要.按该方法分析结果如表1,其中:Ki表示同一列水平号为i的目标函数值之和；ki=Ki/s,s为任意一列上各水平出现的次数,s=4;极差R=max(ki)-min(ki).从表1中可以看出:

1)由直观分析法可得到影响船体舷侧碰撞区域板架耐撞性能的结构参数主次顺序依次为:腹板高度、外板厚度和腹板厚度.外板厚度和腹板高度所对应的极差差别不是很大,说明了两者对结构耐撞性能的影响是基本相当的,从数据上显示腹板高度的影响稍微大点.

2)目标函数值越大,结构的耐撞性能就越好,在直观分析中表现为每列中k1,k2,k3,k4中的最大值所对应的那个水平就是该因素的较优水平.因此,在该碰撞工况下,舷侧结构的优良尺寸组合为:外板厚度13.0 mm,腹板厚度11.0 mm,腹板高度340.0 mm.该设计方案是直观分析得出的较优方案.

该方案并不包含于原来的16种试验设计中,因此要对该方案进行有限元计算验证,计算结果如表2,可发现目标函数值比原设计有较大提高,单位质量吸能有所增加,单位质量的位移变形有所降低.与16组正交试验的目标函数值相比,该方案对应的目标函数值不是最大值,因此,方案2才是相对较优的方案.造成这个结果的原因可能是正交试验设计各因素(变量)之间存在不可忽略的交互作用[4];其次,在有限元数值计算过程中可能也存在一定的误差,也给计算结果带来一定的影响.

表1 船体碰撞正交试验及直观分析Table 1 Orthogonal design of ship collision and direct analysis

2.3 BP-GA优化分析

利用文中提出的BP-GA优化方法,对该结构进行耐撞性能优化分析.首先利用BP神经网络对表1中正交试验数据进行学习训练.网络设计时,采用3层网络结构,其中输入神经元3个,隐层神经元7个,输出神经元2个,训练函数为trainlm函数,训练总步数为300,均方差目标为10-4.图4为BP神经网络训练时的均方差变化曲线,从中可以看出,经过22步的迭代计算,训练均方误差已经收敛,达到了预定的精度10-4.第2步是利用改进过后的遗传算法对结构进行优化分析.在遗传算法参数设置中,初始种群规模数为100;采用二进制编码,染色体长度为9;采用自适应交叉和变异算子;最大遗传代数为500代.图5是遗传算法适应度变化的曲线,可以看出,经过约50代的遗传,算法已经找到了最佳适应值,即找到了最优解.

图4 神经网络训练误差收敛曲线Fig.4 Error convergence curve of training net

图5 遗传算法适应度变化曲线Fig.5 Fitness convergence curve of GA

优化结果以及各目标值如表2.BP-GA中外板厚度为13 mm,比原设计减少2 mm;腹板厚度为9.5 mm,比原设计减少0.5 mm;腹板高度为358 mm,比原设计减少2 mm.原设计的目标函数值为0.499,经过优化之后,目标函数值为0.590,比原设计提高了18.24%.BP-GA优化设计目标函数值比原始设计和直观分析优化设计要高出很多,结构质量比原设计减少9.96%(1 320 kg),比直观分析优化设计减少1.25%(151 kg),可见,通过BP-GA优化分析之后,结构质量有较大降低,材料的利用率有较大提高,生产成本必然会降低;从单位质量吸能和单位质量变形倒数的隶属度值上可以看出,相比原始设计和直观优化设计,单位质量吸能指标有很大提高,说明结构吸能的效率很好;而单位质量的变形倒数隶属度指标上有较大的降低,说明在该设计下,结构单位质量发生的变形比前两种设计相对要大些,由于目标函数中f(βE)和f(1/βC)前的加权系数均为0.5,综合之后的目标函数值比原始设计和直观分析优化结果要好,但如果目标中各指标的加权系数发生变化,则将会对优化结果产生一定的影响.

表2 优化结果与目标函数Table 2 Optimized results and objective values

从表2中也可以看出,文中BP-GA优化方法得到的目标函数值比直观分析优化结果提高了约4.61%.主要有以下几个原因:首先,正交试验设计只能在这些离散的水平值中寻找优秀设计方案,但文中BP-GA优化方法能够突破只在这些离散值中取值这个瓶颈,能够在设计变量的范围之内寻找到优秀的设计方案,即全局范围之内的设计方案,表2中BP-GA优化得到的腹板厚度是9.5 mm、腹板高度为358 mm,这两个取值均不在离散水平值中,但该设计的目标函数值却比直观分析的优化结果要好;其次,直观分析是从极差值上寻求设计变量的重要性并确定优化方案的,不免会遇到设计变量之间的交互作用,从而对优化效果造成一定的影响,但文中BP-GA优化方法利用神经网络训练正交设计的试验点,其强大的容错能力和泛化能力使得变量之间的相互影响大大降低,因此,利用该方法进行优化分析往往能得到更好的优化结果.

为验证BP神经网络响应面近似模型的预报精度,利用MSC/Dytran软件计算了BP-GA优化设计所对应的结构响应有限元计算值.建模方式以及材料等有限元数值仿真技术与前面相同.表3给出了程序计算值与优化设计所对应的有限元计算值之间的比较情况,通过对比吸能、单位质量变形的倒数以及整体的目标函数值可以看出相对误差都在10%以内,误差结果可以接受,这反映了BP神经网络响应面近似模型具有良好的精度,同时也说明了文中BP-GA优化方法的计算结果具有较高的精度,优化结果可信有效.

表3 优化结果与有限元计算值比较Table 3 Comparison between optimized results and FEM values

3 结论

文中提出了基于正交试验设计、神经网络、遗传算法的船体结构耐撞优化设计方法,并利用该方法针对某工况下的某船舷侧结构,分析设计变量、约束条件,结合塑性变形及吸能指标建立目标函数,形成结构耐撞性能优化数学模型,开展耐撞结构设计,实现了在耐撞结构设计中的应用,为结构耐撞性优化设计提供了一种新思路.主要得到以下结论:

1)将正交试验设计、神经网络和遗传算法结合起来能够优势互补,实现结构的耐撞性优化设计.计算表明,该方法能够获得具有最佳耐撞性综合指标的结构设计,显示了该方法的优越性.

2)基于船舶碰撞结构的吸能和塑性变形情况,提出了能反映结构耐撞性能优劣的综合指标,分析表明该指标的合理性.不同的约束与加权系数将会对优化产生影响,会得到不同的优化结果.

3)直观优化分析方法只能在正交表离散的水平值中选取设计方案,该方案不一定是全局最优的;BP-GA优化方法能够突破这个瓶颈,找到全局最优解.算例表明,BP-GA优化设计使目标函数相对原设计提高约18.5%,比直观分析提高4.61%.

4)直观分析得出影响舷侧结构耐撞性能的主次因素为肋骨腹板高度、舷侧外板厚度、肋骨腹板厚度.这表明在该工况下肋骨腹板高度对于耐撞性是最敏感的设计变量,直接影响耐撞性综合指标的大小，适当提高腹板高度可以提高耐撞性能.

5)BP神经网络的泛化能力较强,且能在一定程度上克服正交试验设计各因素之间的交互作用.

[1] 张延昌,刘昆,王自力.基于不同形式和刚度撞击船艏的舷侧结构碰撞性能研究[J].江苏科技大学学报:自然科学版,2010,24(5):423-427.

Zhang Yanchang,Liu Kun,Wang Zili.Collision capability of side structure under different forms and stiffness of striking bows[J].JournalofJiangsuUniversityofScienceandTechnology:NaturalScienceEdition,2010,24(5):423-427.(in Chinese)

[2] Hecht-Nielson.Robert[C]∥InternationalConferenceonNeuralNetwork.san Dtego:IEEE,1987:11-13.

[3] 刘文卿.实验设计[M].北京:清华大学出版社,2005.

[4] 李雁云,胡传荣.试验设计与数据处理[M].北京:化学工业出版社,2005.

[5] 李烁,徐元铭,张俊.复合材料加筋结构的神经网络响应面优化设计[J].机械工程学报,2006,42(11):115-119.

Li Shuo,Xu Yuanming,Zhang Jun.Neural network response surface optimization design for composite stiffened structures[J].ChineseJournalofMechanicalEngineering,2006,42(11):115-119.(in Chinese)

[6] 郭海丁,路志峰.基于BP神经网络和遗传算法的结构优化设计[J].航空动力学报,2003,18(2):216-220.

Guo Haiding,Lu Zhifeng.Structure design optimization based on BP-neural networks and genetic algorithms [J].JournalofAerospacePower,2003,18(2):216-220.(in Chinese)

[7] 王自力,朱学军,顾永宁.船体结构耐撞性优化设计方法研究[J].中国造船,2000,41(2):35-40.

Wang Zili,Zhu Xuejun,Gu Yongning.Application of optimization methord to ship structural crashworthiness [J].ShipBuildingofChina,2000,41(2):35-40.(in Chinese)

[8] 傅立军,包忠诩,陈泽中,等.正交试验、神经网络和遗传算法的结合[J].南昌大学学报:工科版,2003,25(1):79-82.

Fu Lijun,Bao Zhongyi,Chen Zezhong,et al.Combination of orthogonal experimental,neural network and genetic algorithms [J].JournalofNanchangUniversity:Engineering&Technology,2003,25(1):79-82.(in Chinese)

[9] 张德丰.MATLAB神经网络应用设计[M].北京:机械工业出版社,2009:92-128.

[10] 于志刚,宋申民,段广仁.遗传算法的机理与收敛性研究[J].控制与决策,2005,20 (9):971-980.

Yu Zhigang,Song Shenming,Duan Guangren.On the mechanism and convergence of genetic algorithm [J].ControlandDecision,2005,20 (9):971-980.(in Chinese)

[11] 雷英杰,张善文.Matlab遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2006.

[12] 李洪波,徐元铭,黄英兰.试验设计法与BP-GA算法在复合材料结构优化中的应用[J].飞机设计,2007,27 (3):2-27.

Li Hongbo,Xu Yuanming,Huang Yinglan.The application of experimental design method with BP-GA in the optimization of composite structures[J].AircraftDesign,2007,27 (3):2-27.(in Chinese)

[13] 张延昌,顾金兰,王自力,等.蜂窝夹层板结构抗冲击正交试验优化设计[J].兵工学报,2010,31(s1):77-81.

Zhang Yanchang,Gu Jinlan,Wang Zili,et al.Optimal design of shock-resistant honeycomb sandwich panel by orthogonal test[J].ACTAArmamentarii,2010,31(s1):77-81.(in Chinese)