双螺旋折流板换热器最佳螺旋角的研究

赵忠超,米浩君,成 华,丰威仙,云 龙

(江苏科技大学 能源与动力工程学院,江苏 镇江 212003)

管壳式换热器(shell and tube heat exchanger)又称列管式换热器,是以封闭在壳体中管束的壁面作为传热面的间壁式换热器[1].这种换热器结构较简单，操作可靠,可用各种结构材料制造,能在高温、高压下使用,是目前应用最广的换热器类型.其缺点主要是流动死区大，换热系数小,流动压降大[2].为了解决上述问题，20世纪60年代，研究人员提出了螺旋折流板换热器.螺旋折流板换热器是将折流板布置成近似的螺旋面，使换热器中的壳侧流体呈连续的螺旋状流动，以实现有效降低壳侧的流动阻力以及强化传热的目的.与常用的弓形折流板式换热器相比，螺旋折流板式换热器边界膜层减薄，没有流动死区，污垢沉淀较少，热阻降低，换热系数增大，压降损失减小，抗振性能强[3].提高螺旋折流板式换热器的传热性能，选取合适的螺旋角至关重要，对于双螺旋折流板换热器同样如此.大量的研究文献表明，随着螺旋角的增大，换热器壳侧的沿程阻力会减小，但同时换热系数也会相应减小[4].因此，螺旋折流板式换热器螺旋角的选取应当综合考虑阻力损失和换热系数之间的关系,根据具体情况作出选择.

1 模型

换热器折流板是用来改变流体流向的板，常用于管壳式换热器设计壳程介质流道，根据介质性质和流量以及换热器大小确定折流板的多少.折流板被设置在壳程，它既可以提高传热效果，又能够起到支撑管束的作用.折流板有弓形，圆盘-圆环形，螺旋折流板等形式[5]，其中螺旋折流板有单螺旋和双螺旋两种(图1,2).为了使螺旋折流板能够用于实际生产，一般可以用平面板子的拼接来实现螺旋折流板.在搭接结构中进一步增加搭接距离，当搭接距离为螺距的一半时，原来相邻的两块折流板相对放置，而原来相间的折流板反而连续在一起，形成所谓的双螺旋结构.为了区分，将普通的连续结构称为单螺旋结构[6].

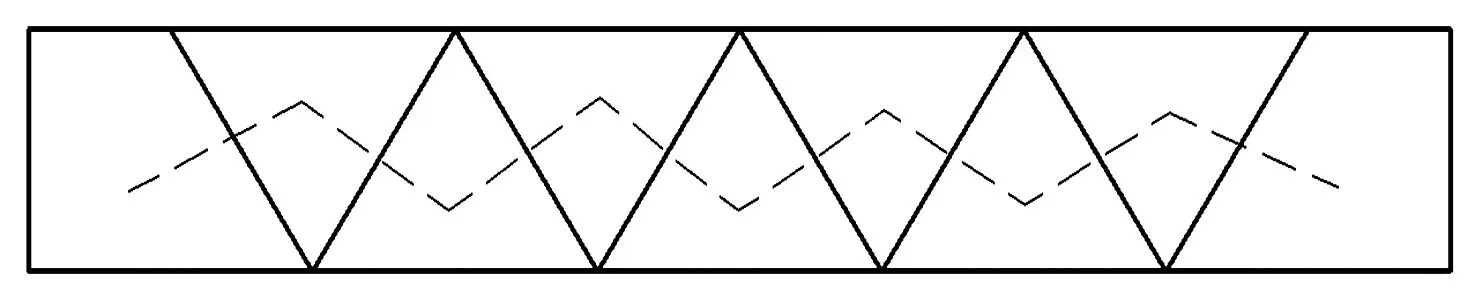
图2 单螺旋换热器结构Fig.2 Structure of single helix heat exchanger

文中建立了管壳式双螺旋折流板换热器模型，在管程介质不变的情况下进行模拟，研究壳程直径对双螺旋折流板式换热器最佳螺旋角的影响.换热器采用单壳程、二管程的非连续形双螺旋折板结构，换热器管束以等边三角形布管.壳程进口温度为90℃，出口温度为50℃；管程进口温度为15℃；管程和壳程进口压力分别为3．1，2．9 MPa.壳程流动工质为润滑油，管程流动工质为水.

在流体力学的计算中，需要计算一些复杂的方程，主要有描写流体的质量守恒方程、能量守恒方程和动量守恒方程(即N-S方程)[1].这些控制方程可以用一个通用的形式来表达：

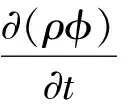
(1)

式中:φ为通用变量,可以代表u,v,w,T等求解变量,Γφ为广义扩散系数,Sφ为广义源项.不同的φ在不同的控制方程中所代表的变量是不相同的[4].

文中换热器内流体以湍流的形式存在,进行数值计算过程中采用最广泛的认可的当属k-ε两方程模型.其中在此模型中，k和ε是两未知量，与之对应的方程为：湍流脉动动能方程(2)和耗散率的控制方程(3).两方程分别得到湍流流动的脉动动能k和湍流耗散率ε，进而求得湍流应力[7].

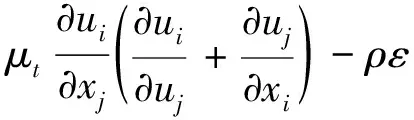
(2)

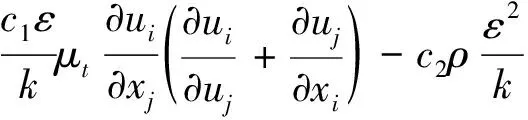
(3)

式中：ui,uj为时均速度，μ为流体动力粘度，μt为湍动粘度，σk和σε分别是与湍动能k和耗散率ε对应的prandtl数，c1和c2为经验常数，通常c1=1.44,c2=1.92.

整个数值模拟的过程,壳程压降与壳程换热系数是主要的性能参数,对于螺旋折流板换热器,壳程对流换热系数ho为[8]:

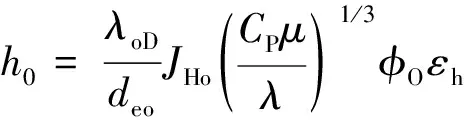
(4)

式中:JHo为壳程传热因子,无因次;CP为壳程流体定压比热容,J/kg·k-1;λoD为壳程材料导热系数,w/(m·k)；λ为壳程流体导热系数,w/(m·k)；φo为壳程壁温校正系数,无因次;εh为旁路档板传热校正系数,无因次.公式的具体含义可查阅文献(7).根据Kerm法推导出螺旋折流板换热器壳程膜传热系数基本形式[7]:

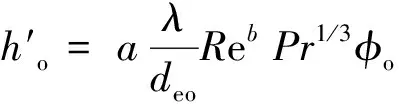
(5)

根据单弓形折流板管内及壳程压力降,结合实际的试验数据推导出螺旋折流壳程压力降近似公式:

(6)

2 不同螺旋角的换热性能对比

在壳体直径为1 400 mm,管长为7 000 m,管径为16 mm,壳侧进出口直径为250 mm,管侧进出口直径为200 mm,管束在正三角排列的情况下,分别选择螺旋角为3°～15°,以1°为步长.在此条件下计算壳程传热系数、压力降，以及不同螺旋角时单位压降下的换热系数.

2.1 壳程换热系数随流量的变化

在相同的几何结构条件下，不同的壳侧进口流量影响对流换热系数.从图3可以看出：在螺旋角θ相同时，双螺旋折流板换热器的壳程对流换热系数k随着壳程进口流量的增大而增大.在流量相同时，双螺旋折流板式换热器壳程对流换热系数h随着螺旋角度的减小而增大.

主要原因是：对于双螺旋折流板换热器，壳体内径、螺旋角及折流板间距三者是相互关联的.当壳体内径一定时，双螺旋折流板间距随着双螺旋折流板的螺旋角的增大而增大，因此，壳程最小截面面积也随之增大.在相同的壳程流量下，最小截面的流速较低，不利于换热.其次，螺旋角越小，流动的切向分量越大，越有利于横向冲刷换热管，减小边界层厚度，增强流体产生湍流，更有利于换热.而且，切向速度分量可使流体产生离心惯性力，在离心惯性力的作用下，产生二次流动，即沿半径方向流动，也使流动扰动大幅度增加，所以增强了换热.

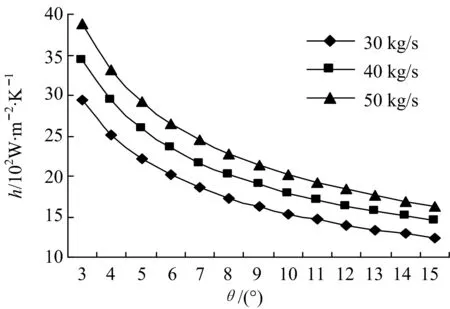
图3 流量与螺旋角对壳程换热系数的影响Fig.3 Influence of flow and helix angle on the heat transfer coefficient

2.2 壳程压降随流量的变化

壳程流速对换热器的换热系数有影响，流速越大，换热器的换热系数就越高.而壳侧的压降对壳侧的流速有影响，壳程压降越少流速越大.从图4可以看出：螺旋角度相同时，双螺旋折流板换热器的壳程阻力Δp随着流量的增大而增大.流量相同时，螺旋折流板换热器的壳程阻力随着螺旋角度的减小而增大.其原因是：流量的增大使边界层变成湍流边界层，边界层分离点提前，管束后面产生大量的漩涡，漩涡运动增强流体径向混合，使得径向速度分布越来越均匀，脉动速度增大；湍动速度越大，壳程压降越大.

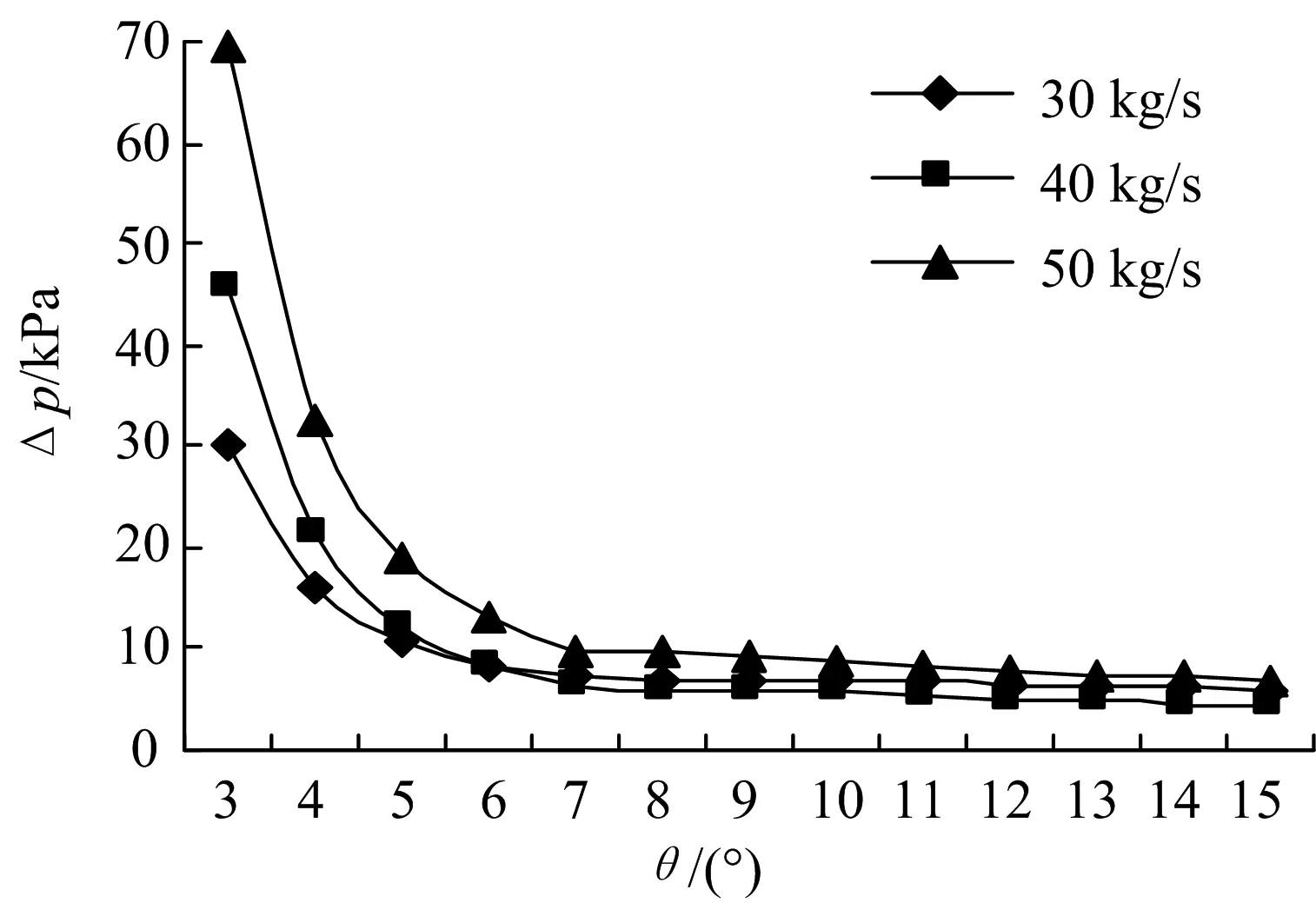
图4 流量与螺旋角对壳程压降的影响Fig.4 Influence of flow and helix angle on the pressure drop

2.3 壳程单位压降换热系数随流量的变化

大量的文献资料表明[9]，随着螺旋角的增大，换热器壳侧的压降会减小，但同时对流换热系数也会相应减小.因此，螺旋折流板式换热器螺旋角的选取应当综合考虑压降和换热系数之间的关系.对流传热的性能不仅取决于流体的速度和物性以及流体与固体壁面间的温差，还取决于流体速度场与热流场之间协同的程度.对流传热的场协同数Fc[10]为：

(7)

式中:Nu为壳程努赛尔数.

场协同数Fc的值代表对流引起的热源强度在全场的总和,反应了整个对流传热过程中速度场与热流场的协同程度,值越大,表明速度场与热流场的协同性越好,传热效果越好.

从图5可以看出：螺旋角度一定时，单位压降下的壳程传热系数随着壳程流量的增加而降低.在不同流量下，壳程场协同数存在最大值，所对应的螺旋角度为6°～8°间，这是最佳螺旋角范围.

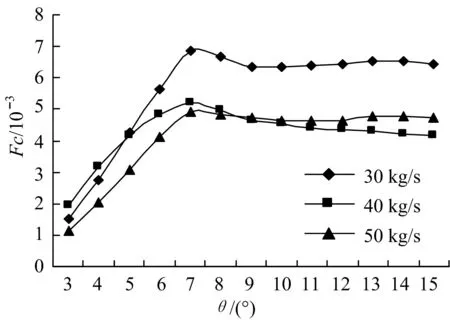
图5 流量与螺旋角对壳程协同角的影响Fig.5 Influence of flow and helix angle on the coefficient of performance

3 不同管长换热器的换热性能对比

在壳体直径为1 400 mm,管径为16 mm,壳侧进出口直径为250 mm,管侧进出口直径为200 mm,管束以正三角排列,流量为30 kg/s的情况下,分别选择管长为7,8,9 m,在此情况下计算壳程传热系数、压力降,以及不同螺旋角条件下的单位压降换热系数.

3.1 壳程换热系数随管长的变化

管壳式换热器的换热管长度与壳径之比有一适合值，不宜太大亦不宜过小.本文以换热器设计标准为参考，管长与壳径的比例在5～10之间选取.从图6可以看出，当壳体直径相同、流量相同、螺旋角相同时，不同管长的换热器的对流换热系数近乎相等，双螺旋折流板换热器的管长对换热器对流换热系数影响甚少.

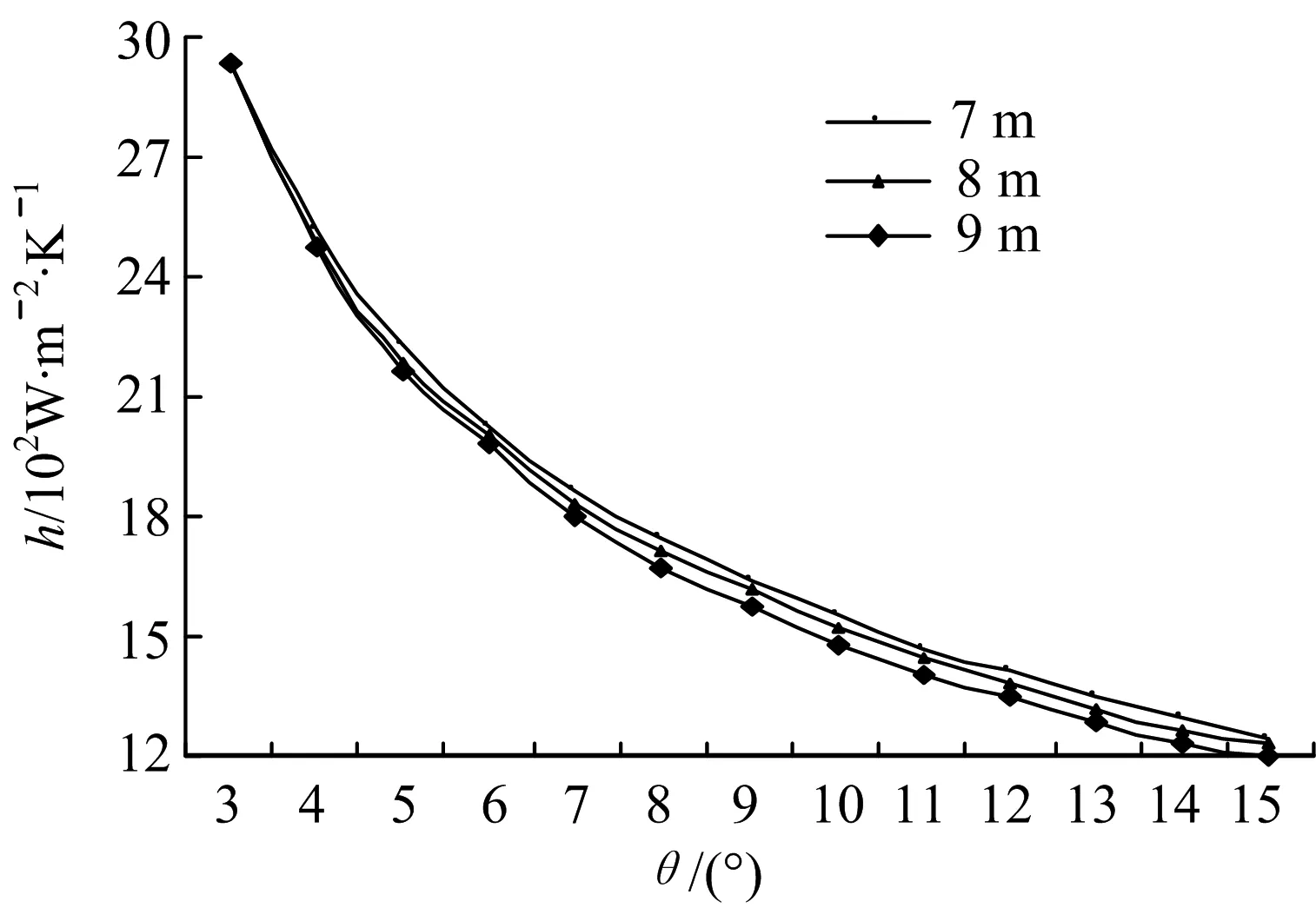
图6 管长与螺旋角对壳程换热系数的影响Fig.6 Influence of tube length and helix angle on the heat transfer coefficient

3.2 单位管长压降随管长的变化

流体经过的路程越长，沿程阻力越大，压降越大.在图7中可以看出，螺旋角度相同时，双螺旋折流板换热器的壳程阻力ΔP随着管长的增大而增大，但随着螺旋角的增大，管子的长度对压降的影响越来越少.因此在适应壳径所对应的管长范围内，螺旋角度越大，管长对换热器的压降影响越少.

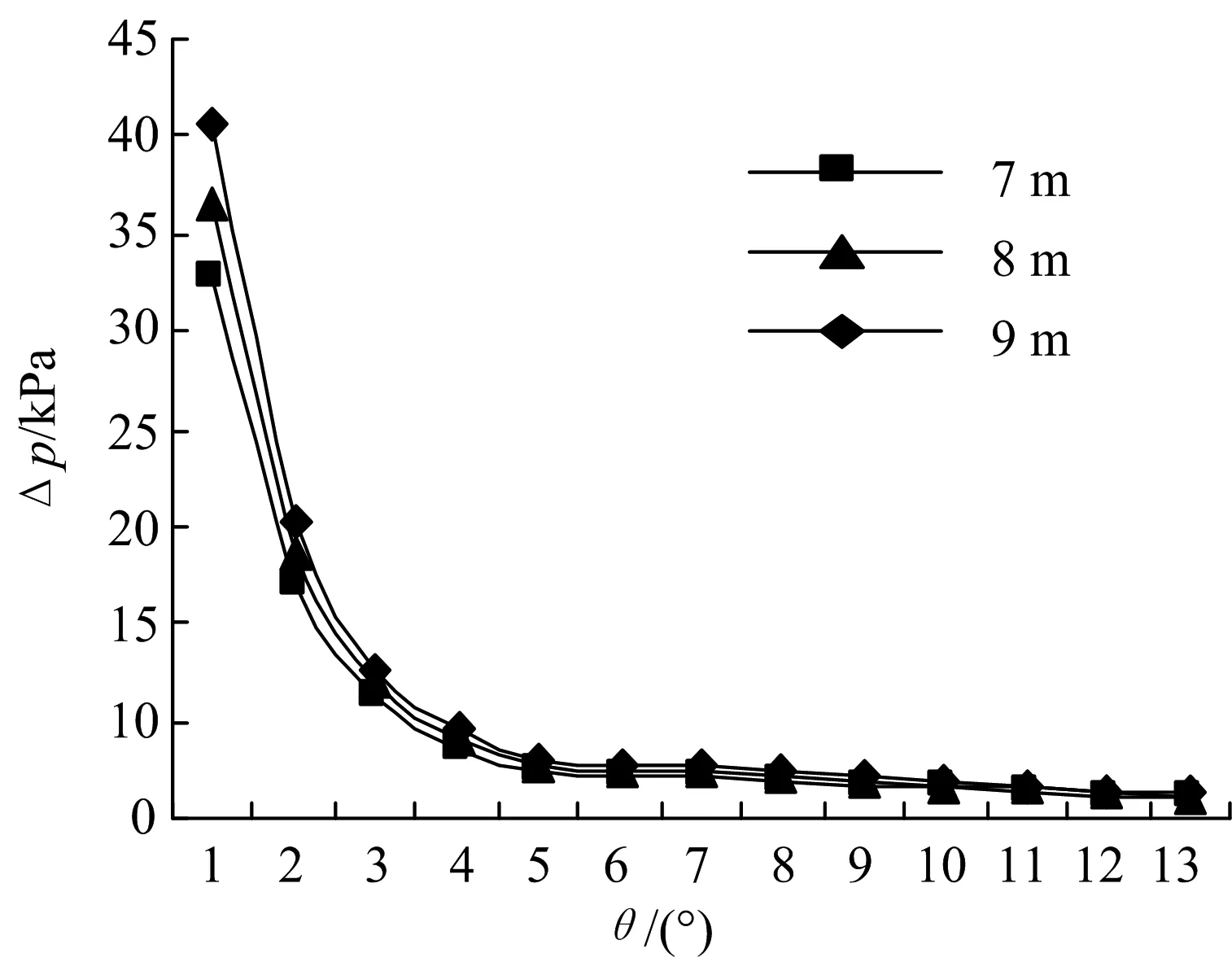
图7 管长与螺旋角对壳程压降的影响Fig.7 Influence of tube length and helix angle on the pressure drop

3.3 壳程单位压降换热系数随管长的变化

文中以单位压降下的换热系数为衡量换热器传热效益的标准，作为性能系数.从图8可以看出：螺旋角度一定时，单位压降下的壳程传热系数随着壳程管长的增加而降低.在不同管长下，单位压降下的壳程传热系数存在最大值.螺旋角在6°～8°间存在一个最佳螺旋角.因此6°～8°是最佳螺旋角范围.由此可知，管长对最佳螺旋角的大小无明显影响.

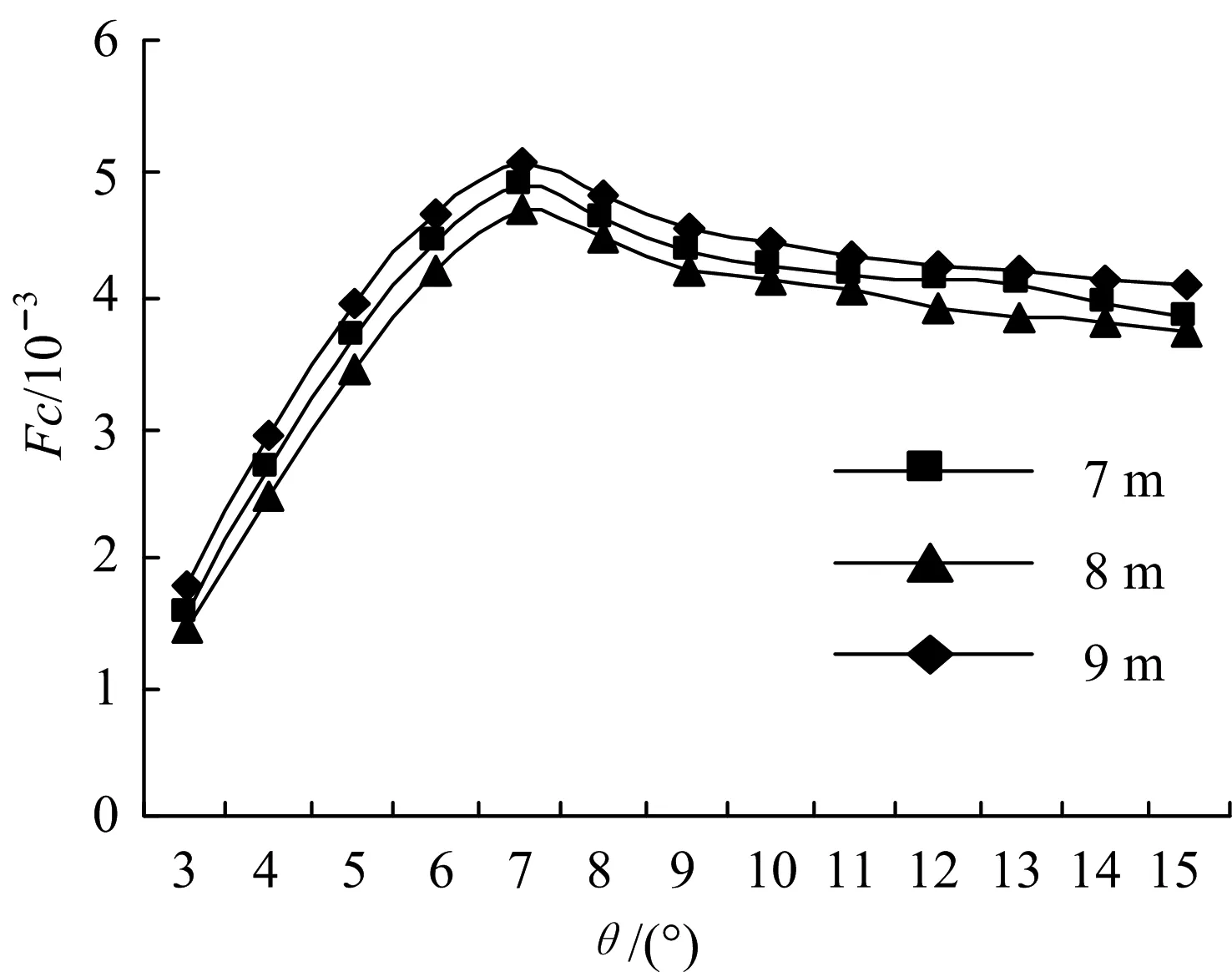
图8 管长与螺旋角对壳程性能系数的影响Fig.8 Influence of tube length and helix angle on the heat transfer coefficient

4 最佳螺旋角随壳体直径的变化

从上文已知,流量一定时,螺旋角小于7°时随着角度的增大单位压降下的换热系数升高;大于7°时随着角度的增大,性能系数下降,流量越小这种规律越明显,这说明6°～8°是壳径R为1 400 mm时的最佳螺旋角范围.流量对最佳螺旋角的大小无明显影响.

用同样的方法模拟了壳径D分别为700,800,900,1 000,1 100,1 200,1 300 mm的螺旋折流板式换热器，发现都有如下规律.图9所示，两线所围区域为最佳螺旋角范围.从图中可看出随着壳径的增大，双螺旋折流板换热器最佳螺旋角范围有下降趋势.

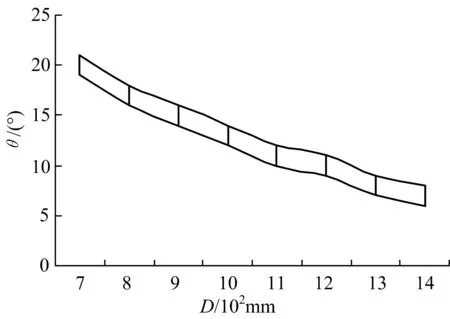
图9 最佳螺旋角随壳径的变化Fig.9 Relationship between shell diameter and optimization helix angle

5 结 论

1) 相同螺旋角度的双螺旋折流板换热器，随着壳程流量的增大压降减小，换热系数增大，壳程性能系数(即单位压降下的换热系数)下降.

2) 壳程流量相同的双螺旋折流板换热器螺旋角度增大，壳程压降减小，壳程换热系数也减小.螺旋角小于最佳螺旋角时，随着螺旋角度的增大，壳程单位压降下的换热系数升高.

3) 壳径一定时，最佳螺旋角一定，壳程流量的改变对最佳螺旋角的大小无影响.壳径一定时，最佳螺旋角一定，壳程流量一定时，管长的改变对最佳螺旋角的大小无影响.

4) 随着壳径的增大，双螺旋折流板换热器的最佳螺旋角有下降趋势.

[1] Wang Qiuwang,Chen Guidong,Chen Qiuyang.Review of improvements on shell-and-tube heat exchangers with helical baffles[J].HeatTransferEngineering,2010,31(10):836-853.

[2] 刘化瑾,陈亚平,李彦晴,等.当量螺旋角对三分螺旋折流板换热器性能的影响[J].化学工程,2010,38(7):22-25,30.

Liu Huajin,Chen Yaping,Li Yanqing,et al.Influence of equivalent helix angle on rerformance of trisection helix baffled neat exchanger[J].ChemtcalEngineering,2010,38(7):22-25,30.(in Chinese)

[3] Peng B,Wang Q W,Zhang C,et al.An experimental study of shell-and-tube heat exchangers with continuous helical baffles[J].JHeatTransfer,2007,129(10):1425-1431.

[4] 钱颂文.换热器设计手册[M].北京:化学工业出版社,2002.

[5] Yang J,Zeng M,Wang Q,et al.Forced convection heat transfer enhancement by porous pin fins in rectangular channels[J].JHeatTransfer-TransASME，2010，132：051702.

[6] Wang Y,Liu Z,Huang S,et al.Experimental investigation of shelland-tube heat exchanger with a new type of baffles[J].HeatMassransfer,2011(47):833-839.

[7] Fan A W,Deng J J,Guo J,et al.A numerical study on thermo-hydraulic characteristics of turbulent flow in a circular tube fitted with conical strip inserts[J].ApplThermEng,2011(31):2819-2828.

[8] Peng B,Wang Q W,Zhang C,et al.An experimental study of shell and tube heat exchangers with continuous helical baffles[J].ASMEJHeatTransfer,2007(129):1425-1431.

[9] Li Y,Jiang X,Huang X,et al.Optimization of high-pressure shell-andtube heat exchanger for syngas cooling in an IGCC[J].IntJHeatMassTransfer,2010(53):4543-4551.

[10] Guo Z Y,TaG W Q,Shah R K.The field synergy principle and its applications in enhancing single phase convective heat transfer[J].InternationalJournalofHeatandMassTransfer,2005,48(9):1797-1807.