二阶变系数线性微分方程可解的研究

李 高，李殊璇，常秀芳

（1.大同大学煤炭工程学院，山西 大同 037003；2.重庆理工大学会计学院11会计信息化1班，重庆 400054）

1 问题的提出

只要能求出二阶变系数齐次线性微分方程的一个特解，则二阶变系数线性齐次或非齐次微分方程的解即可求得［1］。但凡专家学者们进行了大量对二阶变系数次线性微分方程的研究，也没有形成一种操守普遍易行的成规的求解方法，只给出了系数和自由项为特殊类型的二阶变系数线性微分方程的可求解法［2－5］，以及采用构造降阶法求二阶变系数线性微分方程的通解［6］。本文从构造级数解的形式，旨在解决二阶变系数线性微分方程求解的问题，并得出成规求解的方法。

2 方程可解法

假设二阶变系数线性微分方程

设方程 （1）的解为

的级数解形式，其中级数解的系数an为待定的常数。则

将系数和自由项p（x），q（x），f（x）均展开为x的幂级数，把 （2）、（3）、（4）式代入 （1）式，便得一关于x的恒等式，利用待定系数法或比较法比较关于x多项式的同次幂的系数可得an，则即得二阶变系数线性微分方程的级数解y＝∑anxn。

定理 如果二阶变系数线性微分方程

的系数和自由项p（x），q（x），f（x）在零点的某邻域内均可展开为x的幂级数，则方程必有级数解y＝∑anxn。

特别地，系数和自由项p（x），q（x），f（x）含有无理式，在x的某邻域内均展不成x的幂级数，此时取无理式的公倍数m，令x＝tm，则在零点的某邻域内均可展开为t的幂级数，则方程必有级数解y＝∑antn，再把t＝回代，即得方程的解。

3 举 例

例 求微分方程

的通解。

代入方程y″＋xy′＋y＝0，得

比较系数得

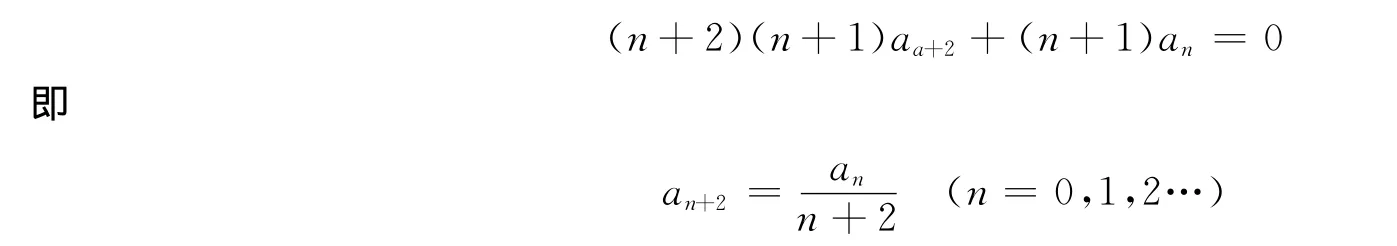
当n＝2k-1时，得

当n＝2k-1时，得

其中a0、a1为任意常数。

［1］王高雄.常微分方程［M］.北京：高等教育出版社，1985：7-28.

［2］常秀芳，李高.伯努利方程的几种新解法［J］.雁北师范学院学报，2007，23（02）：89-91.

［3］李录苹，王通.关于几类二阶微分方程的解法［J］.雁北师范学院学报，2006，22（02）：71-72.

［4］李高，常秀芳.不定方程x2＋y2＋z2＝2（xy＋yz＋xz）的解及其性质［J］.山西大同大学学报，2011，27（03）：6-10.

［5］李高，常秀芳.二阶变系数线性微分方程及其衍生方程［J］.河北北方学院学报：自然科学版，2011，27（05）：13-15.

［6］李高，常秀芳.关于二阶变系数线性微分方程求解法的研究［J］.河北北方学院学报：自然科学版，2010，26（06）：12-19.