对Apriori算法的研究及改进

2013-10-22孙高峰

河北北方学院学报（自然科学版） 2013年2期

丁丽，孙高峰

（1.亳州职业技术学院信息工程系，安徽亳州 236800；2.安徽电力亳州供电公司电力调度控制中心，安徽亳州 236800）

随着信息技术的发展，数据库中存放的信息越来越多，从大量的数据中提取有价值的信息变得越来越难，数据挖掘正是为了满足这种需求应运而生的。数据挖掘（data mining），是从存放在数据仓库、数据库或其他信息库中的大量数据中，寻找有价值信息的过程［1］。数据挖掘又称为数据中的知识发现KDD，即从数据库中发现隐藏的知识［2］。关联是指两个或多个变量值之间存在的相互联系。关联规则挖掘就是寻找给定的大量数据中项集之间存在的某种规律的过程。它是数据挖掘中的一个热点，近几年被广泛研究和应用［3］。关联规则最重要的算法是Apriori算法。关联规则的研究揭示了数据库中事先不知道的、不同项的依赖关系。比如，通过对顾客所购买的商品进行分析，发现购买方便面的顾客很多也同时购买了火腿肠，可以考虑把方便面和火腿肠摆放在一起，可能会增加二者的销售量。

1 关联规则概述

1.1 关联规则的基本概念

所谓关联规则就是形如A＝＞B，表示若A成立则B成立。在进行关联分析时需要计算规则A＝＞B的概率，其实质是一个条件概率P（B︱A）。相关的概念有以下几个：

1）项、项集

项是数据库中不可分割的最小数据单位，一般用i表示。项的集合称为项集，包含K个项的项集称为K项集。设I＝｛i1，i2，…，im｝是项的集合。每个交易T（Transaction）是数据项的一个子集，T⊆I。与任务相关的交易的集合用D表示，对于每一条交易记录记为TID［4］。

2）关联规则

设A是一个项集，当且仅当A⊆T。关联规则是具有A＝＞B的蕴涵式，其中A⊂I，B⊂I，且A∩B＝φ［5］。

3）支持度

支持度用于描述规则的有用性。如果D中有%S的交易记录包含A∪B，则记关联规则A＝＞B的支持度为 %S［6］。即support（A＝＞B）＝ %S＝P（A∪B），最小支持度记为min＿sup。

4）置信度

置信度用于描述规则的确定性。如果D中包含A的交易记录中，有%C也包含B，则记关联规则A＝＞B的支持度为%C。即confidence（A＝＞B）＝%C＝P（B｜A），最小置信度记为min＿conf。

同时满足最小支持度和最小置信度的关联规则称为强关联规则。

5）频繁项集

如果项集A的支持度不小于设定的最小支持度，即support（A）≥min＿sup［7］，则称项集A为频繁项集。频繁1－项集的集合记为L1，频繁K-项集的集合记为Lk。

1.2 关联规则应用实例

例如：设I＝｛A，B，C，D，E｝，某超市数据库中有一组如表1所示的销售记录。表中有8次交易记录，每次交易都记录了一起购买的商品代码。

表1 商品销售数据

表2 L1和支持度计数

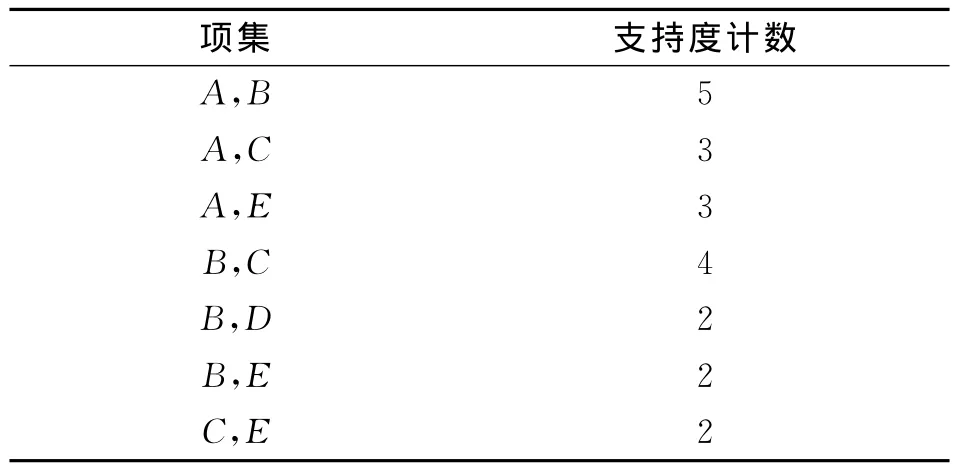
表3 L2和支持度计数

表4 L3和支持度计数

假设关联规则的支持度计数至少为2，即最小支持度为2／8＝25%，则将符合条件的项集和支持度计数列出，如表2，3，4所示。

由项集｛A，B，C｝，可以得到如表5所示的关联规则。

若最小置信度为60% ，则｛A，C｝＝＞｛B｝为强规则。

若最小置信度为50%，则｛B，C｝＝＞｛A｝也是强规则。

表5 关联规则和置信度

2 Apriori算法

2.1 Apriori算法思想

Apriori算法是关联规则中最重要的一种挖掘频繁项集的算法，它是由R.Agrawal和R.Srikant于1994年提出的［8］。它使用层次迭代的搜索方法，由k-项集寻找（k＋1）-项集，被公认为最经典的关联规则挖掘算法。首先，扫描数据库，统计出只有一个元素的项集出现的支持度计数（或称为频数），得出候选1－项集C1，再根据设定的最小支持度计数，把不满足最小支持度计数的项集删掉，得到频繁1－项集L1。然后，由L1统计出包含两个元素的项集，得出候选2－项集C2，扫描数据库，统计C2中每个项集的计数，选择满足最小支持度的项集，得到频繁2－项集L2。接着由L2寻找候选3－项集C3，再由C3得出频繁3－项集L3。重复这个过程，直到找不到频繁K项集LK为止。其过程可以形如：C1→L1→C2→L2→C3→L3→……寻找每个LK都要扫描数据库一次，数据库的大小直接影响Apriori算法的运算速度。Apriori性质：频繁项集的所有非空子集都必须是频繁的［9］。如果项集I不满足最小支持度，则I不是频繁的，如果项A添加到I，则1UA也不是频繁的。也就是说，非频繁项集的超集都是非频繁项集。

Apriori性质可以用于压缩搜索空间，因此可以提高频繁项集挖掘的效率。根据Apriori性质，由LK－1寻找Lk（k≥2）的过程分为以下两步：

（1）连接。将Lk－1与自身连接产生候选K-项集Ck

（2）剪枝。首先，如果Ck的（k-1）项子集不在Lk－1中，则该候选项是非频繁的，把它从Ck中删除。然后，结合最小支持度产生Lk。

2.2 Apriori算法的不足

Apriori算法虽然对候选集的大小进行了压缩，能够比较有效地产生频繁项目集，但在效率上却存在着一定的不足，主要表现为：

（1）数据库重复扫描的次数太多。在由CK寻找LK的过程中，CK中的每一项都需要扫描事务数据库进行验证，以决定其是否加入Lk，存在的频繁K-项集越大，重复扫描的次数就越多。这一过程耗时太大，增加了系统1／0开销，处理效率低［10］，不利于实际应用。

（2）产生的候选集可能过于庞大。如果一个频繁1-项集包含100个项，那么频繁2-项集就有C2100个，为找到元素个数为100的频繁项集，如｛b1，b2，…，b100｝，那么就要扫描数据库100次，产生的候选项集总个数为：

对于一个这样庞大的项集，计算机难以存储和计算，挖掘效率低下。

3 改进的Apriori算法

为了减少数据库的扫描次数、支持度计数的统计量以及大量无用候选项的产生所带来的弊端，提高挖掘的效率，在经典的Apriori算法的基础上提出了改进的Apriori算法。

与国外的机构库建设的高速发展相比，我国目前还处于起步阶段。吴建中[3]2004年初发表文章探讨了机构库对图书馆整体管理模式的冲击，将知识库的概念引入我国。2005年7月，北京大学图书馆率领国内50多所高等院校图书馆联合发表《图书馆合作与信息资源共享武汉宣言》，在宣言中明确指出我国高校图书馆应“建设特色馆藏，开展特色服务，建立一批特色学术机构库（Institutional Depository）”[4]。从那之后，机构知识库的建设在国内，特别是我国高校图书馆逐步开启[5]。

3.1 改进的Apriori算法分析

1）理论基础：Apriori性质及其推论。

性质1：频繁项集的所有非空子集都必须是频繁的。（Apriori性质，记为性质1）

性质2：若频繁K-项集Lk中各个项可以做链接产生Lk＋1，则Lk中每个元素在Lk中出现的次数应大于或等于K，若小于K，则删除该项在Lk中所有的事务集［11］。（Apriori性质的推论，记为性质2）

2）具体实现原理

首先把事务数据库D转化成布尔表，然后转置［12］。转置后的布尔表格中，列表示事务，行表示项集。用逻辑值1和0表示每一个项在每一个事务中的存在与否，1表示存在，0表示不存在。通过对此布尔表进行挖掘运算实现对事务数据库D的挖掘。

3.2 改进的Apriori算法挖掘步骤

1）首先，把事务数据库表转化成布尔表，转置，扫描转置后的布尔表，记录每行1的个数，并存储在列的最右侧，每行中1的个数即为该项的支持度计数，得出候选1－项集C1的集合。再把C1中支持度计数小于最小支持度计数的项所在的行删除，得到简化的事务数据布尔表D1和频繁1－项集L1。

2）链接L1，产生频繁2－项集L2。不需要扫描原数据库，只要扫描D1即可。将D1中每两行按位作逻辑与运算，结果用逻辑值1和0表示，得到2－候选项集的集合C2，然后扫描计数，得出2－项集的支持度计数，删除支持度计数小于最小支持度计数的项，得到D2’和L2’。计算各项在L2’中出现的次数。（要求各项在Lk中出现的次数大于或等于K，若小于K，则删除该项在Lk中所有的事务集。）删除出现次数小于2的项集，得到再次简化的事务数据库布尔表D2和L2。

3）当K≥3时，重复2），直到找到最大频繁项集为止。

此方法不需要重复扫描数据库，支持度计数的统计也比较容易，也不会产生过多的冗余，因此，可以在很大程度上降低挖掘的复杂度，提高挖掘算法的效率。

3.3 改进的Apriori算法描述

3.4 改进的Apriori算法举例

现有一事务数据库表D，如表6所示。设定最小支持度计数为3。

表6 事务数据库表D

表7 布尔表DT

下面是改进的Apriori算法的运行过程。（1）首先将数据库表D转换成布尔表DT，如表7所示。

对表7转置，然后扫描，并记录各个项支持度的个数，得到候选1-项集C1，如表8所示。

表8 候选1-项集C1

表9 数据库表D1

表10 频繁1-项集L1

将C1中不满足最小支持度计数的项｛B｝、｛D｝、｛G｝、｛H｝所在的行删除，得到精简的数据库表D1和频繁1－项集L1，如表9、10所示。

（2）对表D1，每两行求交集，并扫描计数，得到2－候选项集的集合C2’，如表11所示。

表11 C2’

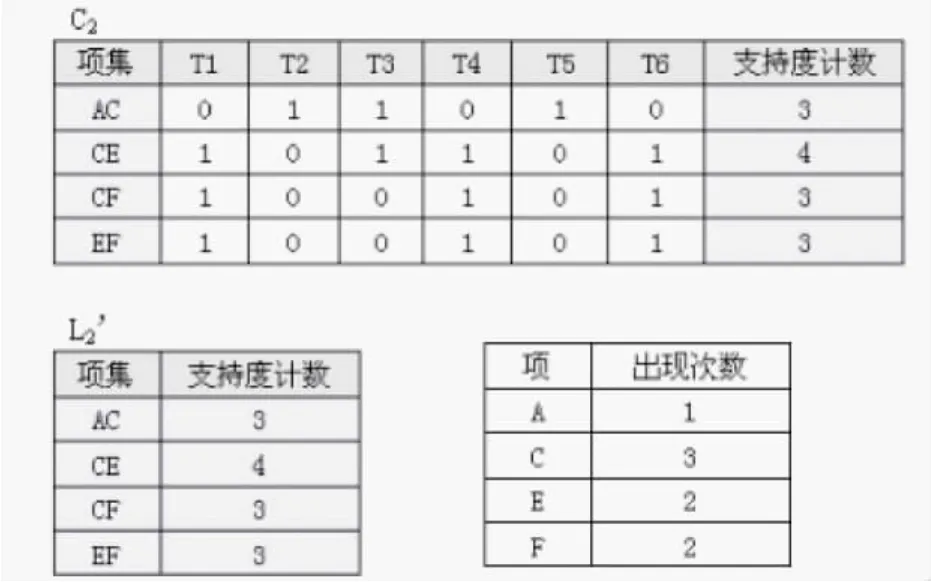
图1 C2、L2’

将C2’中支持度计数小于最小支持度计数的项｛AE｝、｛AF｝所在的行删除，得到C2和L2’，计算各项在L2’中出现的次数，如图1所示。

由于A在L2’中出现的次数小于2，所以应将C2中含A的项，即｛AC｝所在的行删除，得到精简的数据库表D2和频繁2－项集L2，如表12、13所示。

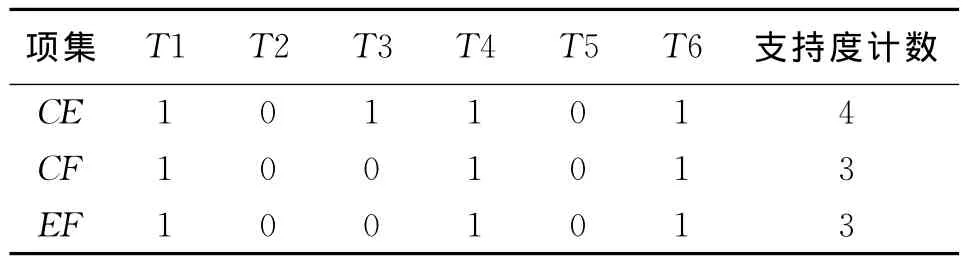
表12 数据库表D2

表13 频繁2－项集L2

（3）扫描D2，对D2中每两行求交，得到精简的数据库表D3和频繁3－项集L3，如表14、15所示。

表14 数据库表D3

表15 频繁3－项集L3

从以上过程可以看出，改进的算法在计算支持度个数时，每次不需要扫描全部数据库，只需要在精简的数据库表中扫描各项所在的行就可，大大节省了时间；另外，改进的算法在由频繁K-项集生成频繁（k＋1）-项集时，对Lk中元素的个数进行计数处理，根据计数结果删除了出现次数小于K的元素，减少了组合的个数，从而减少了循环判断的次数，提高了运算效率。

4 两种算法的性能比较

为了证实改进的Apriori算法的性能，对改进的Apriori算法和经典Apriori算法的效率进行对比。实验数据来源于亳州职业技术学院图书馆数据库，实验硬件环境CPU为AMD Athlon（速龙）II X2 245双核，内存为4GDDR2 800MHz；操作系统是Windows XP，数据库为Microsoft SQL Server 2000，编辑语言为Visual c＃。性能对比曲线如图2所示。

从图2中可以看出改进的Apriori算法性能优于经典的Apriori算法，尤其在交易事务条数比较多的情况下，效果更加明显。