三维微波加热腔的建模与仿真
2013-10-22孙兴华
孙 鹏,赵 蕾,孙兴华
(1.河北北方学院信息科学与工程学院,河北 张家口 075000;2.河北省张家口市第七中学,河北 张家口 075000)
0 引 言
1947年美国雷声公司研制成世界上第1个微波炉——雷达炉。经过不断改进,1955年家用微波炉才在西欧诞生,20世纪60~70年代,由于辐射安全性、操作方便性等问题的解决,使得微波炉造价不断下降,从而得到进一步推广,逐渐成为家庭生活必备的电器之一。
然而,由于微波加热机理复杂,难于定量分析,再加上缺乏高性能的专用微波化学反应器和微波冶金反应器,限制了如加热效率、均匀性等微波加热性能的进步。
由于多模微波加热腔体的加热效率、均匀性与激励的形状和位置、加热载体电磁特性、溃口搅拌器和样本位置等因素有关,理论分析和数值模拟都极其复杂。国内外虽然有许多学者研究过上述问题,例如:Geedipalli[1]等人利用有限元分析软件ANSYS仿真了转盘对微波加热均匀性的影响;Plaza-González等人[2,3]用FEM方法分析了搅拌器位置对二维微波加热器场分布的影响;Knoerzer等人[4]用Quick-Wave 3D软件模拟了微波加热的均匀性,并用磁谐振成像技术证实了仿真结果;Shou-Zheng等人[5]用解析方法从理论上研究了矩形微波加热器内多层介质中的功率分布;Nott等人[6]用MRI技术和光纤测温法测量了微波炉内样品的温度分布;Pandit等人[7]用计算机可视系统研究了微波消毒处理过程中食品内的冷点和热点分布;Pedreňo-Monlina等人[8]基于自动温度测量设备寻找到了微波炉内被处理材料的最位置;Sundberg和Kopyt等人用FDTD方法[9,10]和FDTD-FEM方法[11]模拟了微波加热过程,但目前仍有许多问题尚待解决。本文使用多物理仿真软件COMSOL Multiphysics进行仿真,由于家用微波炉激励源位置固定,本文只对不同位置加热样本的热吸收效率、不同大小加热样本加热吸收效率和多激励对微波加热均匀性的影响进行了建模与仿真。
1 微波加热腔建模

图1 FEM三维微波加热腔模型
三维微波加热腔模型见图1所示,腔体尺寸为290mm×285mm×200mm3,激励在模型的右侧(x=290mm)平面上,尺寸为109.2mm×54.6mm2,中心坐标为:290mm、107.34mm、41.84mm;样品为正方体,尺寸为25mm3×25mm3×25mm3,位于z=30mm的平面上,中心坐标为145mm、142.5mm、42.5mm;激励源频率为2 450MHz,功率为500W。
采用有限元法,联合求解有源边界条件下的Maxwell方程组和热传导方程,即可计算上述模型的电磁场分布、温度分布、微波加热效率和微波加热均匀性。本文采用基于有限元计算的多物理仿真软件COMSOL Multiphysics进行上述计算。
2 仿真结果与讨论
2.1 样品大小对微波加热效率的影响
对于相同介电常数的样本,不同体积的样本在相同加热条件下的加热效率如表1。数据显示,随着体积的增大,加热效率亦增大。由于现有计算机计算能力的限制,本文只计算到体积为166.4cm3的样本加热效率,更大样本的微波加热率有待进一步验证。

表1 样品体积与微波加热效率的关系
2.2 样品位置对微波加热效率的影响
微波加热腔底面接近正方形,故设置样品初始位置的中心坐标为22.5mm、22.5mm、42.5mm,在z=42.5mm的平面上样品沿x和y轴方向以30mm为间隔,各移动8次,在整个移动过程中一共产生了81个不同位置。计算结果表明,当样品中心坐标为142.5mm、82.5mm、42.5mm时,得到最大微波加热效率91.3%。
2.3 多激励对微波加热均匀性的影响
本文比较了单激励、双激励和三激励时,腔内场分布及样品水平截面温度分布,结果如图2和图3。从图中可以看出,多激励时,腔内的场分布较双激励和单激励有所不同,且样品温度均匀性有一定改善。本文根据公式Uni=(Tmax-Tmin)/Taν计算了样品内温度分布的均匀性,结果表明,单激励、双激励和三激励时Uni分别为67%、18.9%、11%,表明多激励对样品加热温度分布均匀性有一定改善作用。


图2 微波炉内z=42.5mm平面上的电场分布
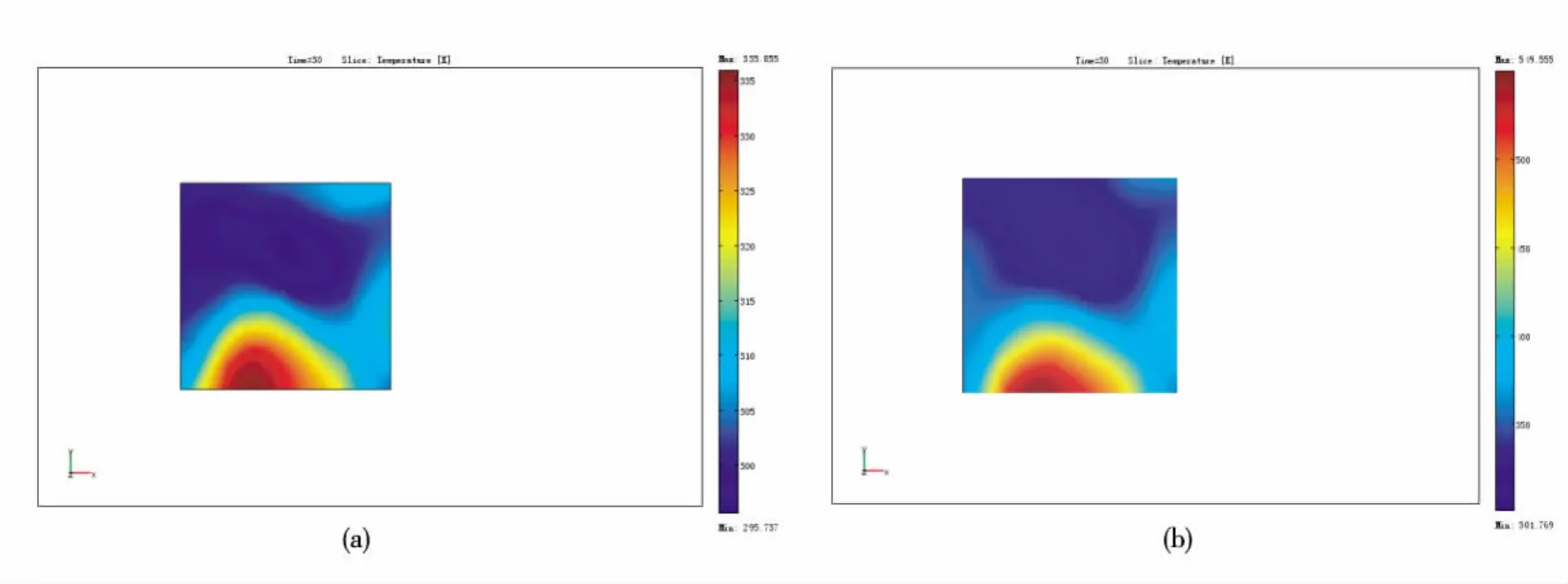

图3 加热样品上表面的温度分布
3 结 论
本文应用多物理仿真软件对微波加热腔在不同条件下的加热情况进行了模拟。样本大小对加热效率有一定的影响,样本越大加热效率越高。样本放在不同的位置时,加热效率也不同。最后模拟了多激励对样本温度均匀性的影响。以上结论均对商用及家用微波加热器的设计与使用具备一定的参考价值。进一步的研究应该结合具体实验,将仿真软件的仿真结果与实际微波加热设备进行对比,从而进一步验证仿真结果。
[1]Geedipalli S S R,Rakesh V,Datta A K.Modeling the heating uniformity contributed by a rotating turntable in microwave ovens[J].J Food Engin,2007,82:359.
[2]Plaza-González P,Monzó-Cabrera J,Catalá-Civera J M,et al.A new approach for the prediction of the electric field distribution in multimode microwave-heating applicators with mode stirrers[J].IEEE Trans Magn,2004,40(05):1672.
[3]Plaza-González P,Monzó-Cabrera J,Catalá-Civera J M,et al.Effect of mode-stirrer configurations on dielectric heating performance in multimode microwave applicators[J].IEEE Trans Microw Theory Tech,2005,53(05):1699.
[4]Knoerzer K,Regier M,Schubert H.Microwave heating:a new approach of simulation and validation[J].Chem Eng Tech,2006,29(07):796.
[5]Shou Z Z,Han K C.Power distribution analysis in rectangular microwave heating applicator with stratified load[J].J Microw Power Electrom Energy,1988,23(02):139.
[6]Nott K P,Hall L D.Validation and cross-comparison of MIR temperature mapping against fiber optic thermometry for microwave heating of foods[J].Intern J Food Sci Tech,2005,40(07):723(2005).
[7]Pandit R B,Tang J,Liu F,et al.A computer vision method to locate cold spots in foods in microwave sterilization processes[J].Pattern Recogn,2007,40:3667.
[8]Pedreňo-Molina J L,Monzó-Cabrera J,Pinzolas M.A new procedure for power efficiency optimization in microwave oven based on thermographic measurements and load location search[J].Intern Commun Heat Mass Transf,2007,34:564.
[9]Sundberg M,Risman P O,Kildal P S,et al.Analysis and design of industrial microwave ovens using the finite difference time domain method[J].J Microw Power Electrom Energy,1996,31:142.
[10]Kopyt P,Celuch-Marcysiak M.FDTD modeling and experimental verification of electromagnetic power dissipated in domestic microwave ovens[J].J Telecomm Inform Tech,2003,1:59.
[11]Kopyt P,Celuch-Marcysaik.Coupled FDTD-FEM approach to modelling of microwave heating process[C].IEEE Confer Public,2004,171.
