基于PCA-ARIMA模型的高血压发病率预测
2013-10-22马亮亮
马亮亮
(攀枝花学院数学与计算机学院,四川 攀枝花 617000)
近些年,ARIMA、ARMA等经典时间分析方法在股票、网络流量、害虫发生、发病率等时间序列中得到了广泛的应用[1-4]。ARMA模型极具弹性,可以表示各种不同类型的时间序列预测模型,融合了时间序列分析和回归分析的优点,在时间序列预测中得到了广泛的应用[5]。然而时间序列受多种因素综合影响,是一种非常复杂的非线性变化系统,基于线性建模的ARMA难以准确描述时间序列的非线性变化规律,导致预测结果不理想[6]。
实际科学研究中经常遇到多个指标的实际问题,虽然含有多个指标的数据可以提供丰富的信息,但同时增加了分析问题的复杂性和难度,而且事实上,不同指标之间往往存在一定的相关性。那么,能否有一种合理的方法,即用较少的几个相互独立的指标来代替原来的多个指标,使其既减少了指标的个数,又能综合反映原指标的信息?回答是肯定的,主成分分析 (principal component analysis,PCA)就是用于解决此类问题的一种处理方法。
为了有效利用各种时间序列预测模型的优点,克服单一模型的缺陷,一些学者基于著名的M-竞争理论提出了时间序列组合预测模型,实证结果表明,相对于单一模型,组合预测模型能够较大限度地利用预测样本的各种信息,大幅度地提高时间序列的预测精度,比单一模型考虑的问题更系统、更全面[7-8]。
为了提高时间序列的预测精度,考虑时间序列的环境影响因子,本文将主成分分析 (principal component analysis,PCA)和ARIMA相融合,产生一种新的时间序列组合预测模型-PCA-ARIMA,并通过高血压发病率对PCA-ARIMA预测性能进行验证。
1 PCA-ARIMA模型预测原理
PCA-ARIMA模型的预测原理为:首先利用PCA对时间序列的影响因子进行筛选,只保留对系统影响较大的变量,然后采用ARIMA模型对保留变量进行预测和建模。PCA-ARIMA具体的预测流程如图1所示。

图1 PCA-ARIMA模型的预测流程
2 评价指标和参比模型
为了评价PCA-ARIMA模型性能的优劣,选择PCA-MLR、ARIMA作为参比模型,其中PCA-MLR表示首先采用PCA进行影响因子筛选,然后采用多元线性回归 (multiple linear regression,MLR)进行建模和预测;ARIMA表示直接采用ARIMA模型进行建模和预测,并使用均方误差 (mean square error,MSE)和平均相对误差 (mean absolute percentage error,MAPE)作为模型的评价指标。MSE和MAPE分别定义如下:
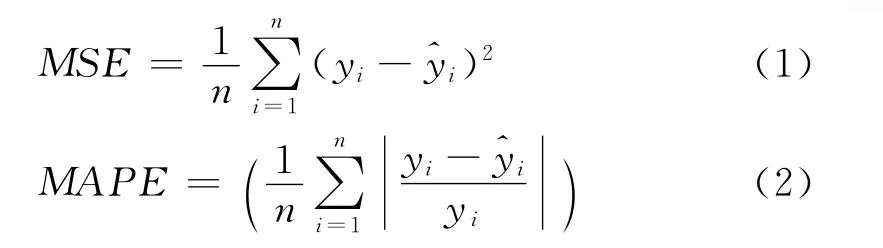
其中yi表示时间序列的实际值表示模型的预测值,n表示测试样本数。
3 实证研究
3.1 数据来源
数据资料来源于甘肃省天水市疾病预防控制中心提供的1999年1月至2005年12月高血压发病率(y)。高血压发病率的气象影响因子有:月平均气压x1(pha),月平均气温x2(℃),月平均相对湿度x3(%),月平均风速x4(m/s),月降水量x5(mm)。
3.2 主成分分析 (PCA)
利用气象影响因子:月平均气压x1,月平均气温x2,月平均相对湿度x3,月平均风速x4,月降水量x5做主成分分析,得主成分的统计信息如表1所示。

表1 主成分统计分析
从主成分分析结果可知,第一主成分的特征根为2.664,它解释了总变异的52.883%;第二主成分的特征根为1.500,它解释了总变异的30.003%;前两个特征根均大于1,累计贡献率82.886%。由于第三个主成分的特征根较接近于1,故宜取前三个主成分,此时累计贡献率达93.698%。
前三个主成分与各个变量x1,x2,x3,x4,x5的关系如下:
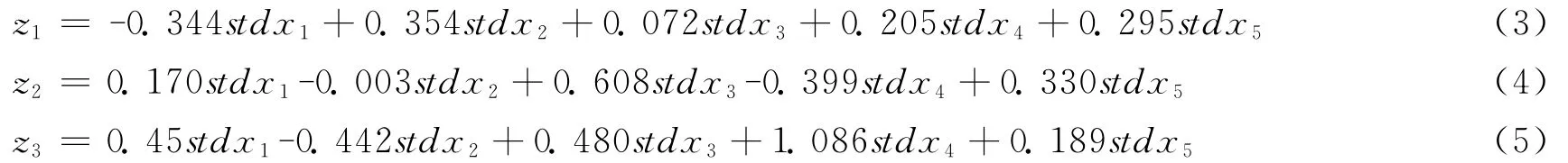
其中stdxi(i=1,2,3,4,5)表示标准指标变量:

3.3 因子筛选
从主成分分析结果可知,影响高血压发病率变化的因子有很多,而这些因子之间可能存在多重共线性,特别是当各个解释变量之间存在着高度的相互依赖关系时,就会给回归系数的估计带来不合理的解释[9]。
为了得到一个可靠的预测模型,需要从众多影响因子中挑选出对高血压发病率变化贡献率大的影响因子,本文采用PCA对影响因子进行筛选。采用SPSS11.5对高血压发病率进行主成分分析,表明前三个主成分包含了原有5个指标93.698%的信息,故采用前三个主成分(z1,z2,z3)代替原有的5个变量(x1,x2,x3,x4,x5)进行建模和预测。
3.4 结果与分析
3.4.1 MLR拟合
运用PCA筛选的对高血压发病率影响显著的前三个主成分:z1,z2,z3采用 MLR进行预测,采用SPSS11.5实现,得到的线性回归方程为:
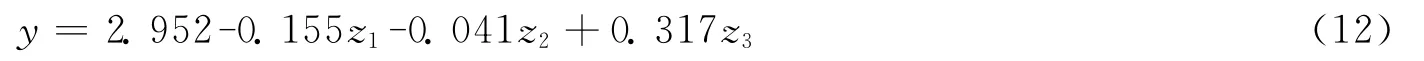
将式 (3) -(5)的z1,z2,z3表达式代入式(12),得到因变量y与标准自变量stdx1~stdx5的线性回归方程:

将标准自变量还原为原自变量,得到因变量y与原自变量x1~x5的线性回归方程为:
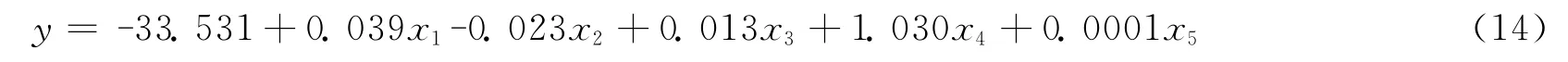
模型主要参数为:相关系数r=0.892;F=2.138;显著水平P=0.0413<0.05,表明建立的线性方程达到显著性要求,该方程可以进行预测应用。
3.4.2 ARIMA拟合
利用高血压发病率(y)绘制该序列的样本自相关分析图,可知当p=1,d=1,q=2时,模型的预测精度最高,可达94.50%。由此可见,ARIMA模型的进行高血压发病率预测的效果好于PCA-MLR预测效果,主要是经过对样本测试集进行差分处理后,序列的趋势性等基本消除,序列更接近于平稳,波动性减小,因此预测效果更佳。ARIMA(1,1,2)模型对应的方程为:
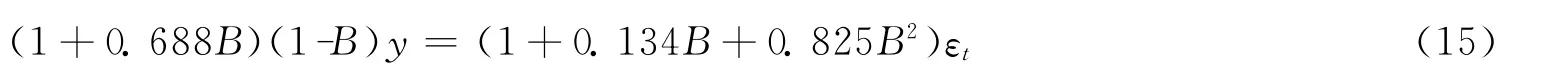
式中随机项εt是相互独立的白噪声序列,且服从均值为0,方差为σ2的正态分布。
3.4.3 PCA-ARIMA拟合
运用经过PCA筛选的前三个主成分(z1,z2,z3)建立PCA-ARIMA模型,得到训练样本集的预测模型PCA-ARIMA(1,1,2):
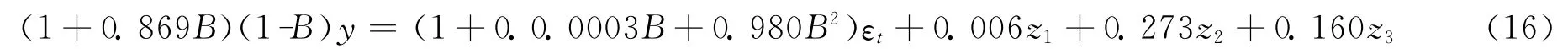
将式 (3) -(5)的z1,z2,z3表达式代入式(16),得到因变量y与标准自变量stdx1~stdx5的PCA-ARIMA(1,1,2):

将标准自变量还原为原自变量,得到因变量y与原自变量x1~x5的PCA-ARIMA(1,1,2)方程为:

各种预测模型拟合的MSE和MAPE见表2。
从表2的对比结果可知,在所有模型中,PCA-ARIMA模型拟合精度最高,误差最小,结果表明,PCA-ARIMA首先采用PCA对高血压发病率的影响因子进行主成分分析,然后采用ARIMA进行建模,能更加准确描述高血压发病率的变化规律,有效地提高了高血压发病率的拟合精度。

表2 各模型的拟合性能比较
3.5 几种模型预测结果对比
由于评价一个预测模型的好坏,主要考察其预测能力而非回代拟合结果,因此,再分别采用PCAMLR、ARIMA、PCA-ARIMA模型进行独立预测,把数据分两部分:1999年1月至2004年12月的数据作为训练集,2005年1月至12月的数据作为测试集,以便获得实际高血压发病率建模精度与预测能力的评定。几种模型对高血压发病率进行学习的预测结果如表3所示。
从表3可知,线性MLR模型和ARIMA模型的预测效果较差,主要是因为它们均只能反映高血压发病率的片段信息,不能全面捕捉到高血压发病率的动态变化规律;而组合预测模型PCA-ARIMA与MLR和ARIMA相比,预测精度有了较大的提高,由于组合预测模型能够充分利用时间序列数据中的信息,并对高血压发病率变化规律进行深入挖掘,避免了单一模型的局限性,其对高血压发病率的预测结果有了较为明显的提高。

表3 几种模型对2005年高血压发病率的预测结果
4 小 结
时间序列受到众多因子的影响,呈现高度非线性变化规律,难以建立精确的数学模型,利用ARIMA模型本身的优点,将PCA引入到时间序列建模中,建立一种时间序列组合模型PCA-ARIMA,并应用于高血压预测中。实例结果表明,PCAARIMA模型简单、容易实现、速度快,而且提高了高血压发病率预测准确率,较好地揭示了高血压发病率的变化规律[5]。
[1]马亮亮,田富鹏.基于非对称ARCH模型的海西州地区支气管炎发病情况研究[J].科技导报,2009,27(24):51-55.
[2]马亮亮,田富鹏.ARMA模型在胆结石发病率预测中的应用[J].军事医学科学院院刊,2010,34(05):1-4.
[3]马亮亮,田富鹏.时间序列分析方法在胆囊炎发病率预测中的应用[J].中华实验外科杂志,2010,27(06):779.
[4]马亮亮,田富鹏.不同时间序列分析方法在高血压发病率预测中的应用[J].中国老年学杂志,2010,30(13):1777-1780.
[5]向昌盛.基于支持向量机的时间序列组合预测模型[D].长沙:湖南农业大学,2011.
[6]罗盛健.基于人工神经网络的刚竹毒蛾发生面积的预测模型[J].华东昆虫学报,2006,15(01):37-39.
[7]Salgdo R M,Pereira J J F,Ohishi T.A hybrid ensemble model applied to the short-term load forecasting problem[A].International Joint Conference on Neural Networks[C].Vancouver:B C Canada,2006,10:2627-2634.
[8]Vila J P,Wagner V,Neveu P.Bayesian nonlinear model selection and neural network:A conjugate prior approach[J].IEEE Trans Neural Netw,2000,11(02):265-278.
[9]马亮亮,田富鹏.逐步回归分析在糖尿病发病情况中的应用[J].渤海大学学报,2009,30(04):321-324.
