影响葡萄酒质量的理化指标分析
2013-10-22刘家保陈中华李云云
刘家保,陈中华,李云云
(1.安徽新华学院公共课教学部,安徽 合肥 230088;2.安徽新华学院商学院,安徽 合肥 230088)
1 引 言
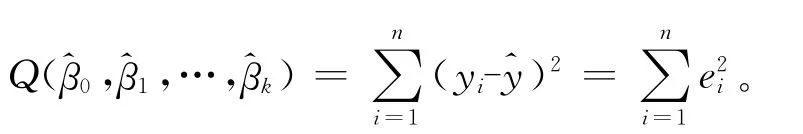
解决问题的思路是根据样本数据,求出参数βj的估计值(j=0,1,…,k),从而得到y对x1,…,x2,xk的线性回归方程。根据品酒员给出的外观、口感、香气、平衡/整体的分数将葡萄酒划分为差、较差、尚好、较好、很好5个等级,根据得票数,建立模型。最后通过线性回归方程,得出各种理化指标对葡萄酒等级的影响。
2 模型的建立与求解
选择10个专业品酒员分别对红葡萄酒27个酒样品和白葡萄酒28个酒样品进行打分,打分的规则为外观分析15分 (包括澄清度5分和色调10分),香气分析30分 (包括纯正度6分、浓度8分和质量16分),口感分析44分 (包括纯正度6分、浓度8分、持久性8分和质量22分)和平衡/整体评价11分。通过10个专业品酒员的打分求其每个酒样品的平均分,如表1所示。

表1 酒样的平均分
2.1 葡萄酒等级划分标准
由上述的评分,确定酿酒葡萄的等级质量由外观分析、香气分析、口感分析和平衡/整体评价4个因素构成,即X= [口感、外观、香气、平衡/整体]对每个因素的评价按差、较差、尚好、较好、很好5个等级 (或按百分制)评定,即Y= [差 (40~50分),较差(50~60分),尚可(60~70分),较好(70~80分),很好 (80分以上)]。采用强制决定法确定各质量因素的权重,分别为口感44%,外观15%,香气30%,平衡/整体11%,即A= [0.44,0.15,0.3,0.11]。
按照评分标准,用MATLAB绘出差、较差、尚好、较好和很好这5个等级的得票数,如图1、图2所示。
2.2 数学模型的建立
葡萄酒等级的划分主要从花色苷、单宁和总酚[7]等方面进行评价,将酿酒葡萄和葡萄酒的理化指标各成分用数学变量依次表示为x1,x2,…,xk。
(1)设随机变量y与一组 (k个)变量x1,…,x2,xk有关系:

其中ε是随机项,服从正态分布N(0,∂2)。
如果 (y1;x11,x21,…,xk1),…,(yn;x1n,x2n,…,xkn)是一个容量为n的样本,

图1 红葡萄各酒样品的得票数

则有:其中β0,β1,…,βk为未知参数,写成矩阵形式为:

其中:

(2)使用因变量的观察值与估计值之间的离差平方和达到最小来求β0,β1,…,βk,

解决问题的思路是根据样本数据,求出参数βj的估计值(j=0,1,…,k),从而得到y对x1,…,x2,xk的线性回归方程:

(3)从表1,2中,可以得到对于红葡萄酒酒样品21、9、23、20、3品评相对较好而对酒样品6、8、15、18、11品评相对较差,对于白葡萄酒酒样品5、9、17、10、28品评相对较好而对酒样品13、12、8、11、16品评相对较差。
2.3 数学模型的简化求解
(1)通过对上述的数据分析,得出影响葡萄酒等级主要受总酚、单宁和总酸参数的影响,对总酚、单宁和总酸参数分别用x1、x2和x3表示,可得线性回归方程为:

(2)求解回归参数的标准方程如下:


图3 红葡萄酒的单宁影响程度图

图4 白葡萄酒的单宁影响程度图

图5 红葡萄酒的总酚影响程度图

图6 白葡萄酒的总酚影响程度图

图7 红葡萄酒的总酸影响程度图
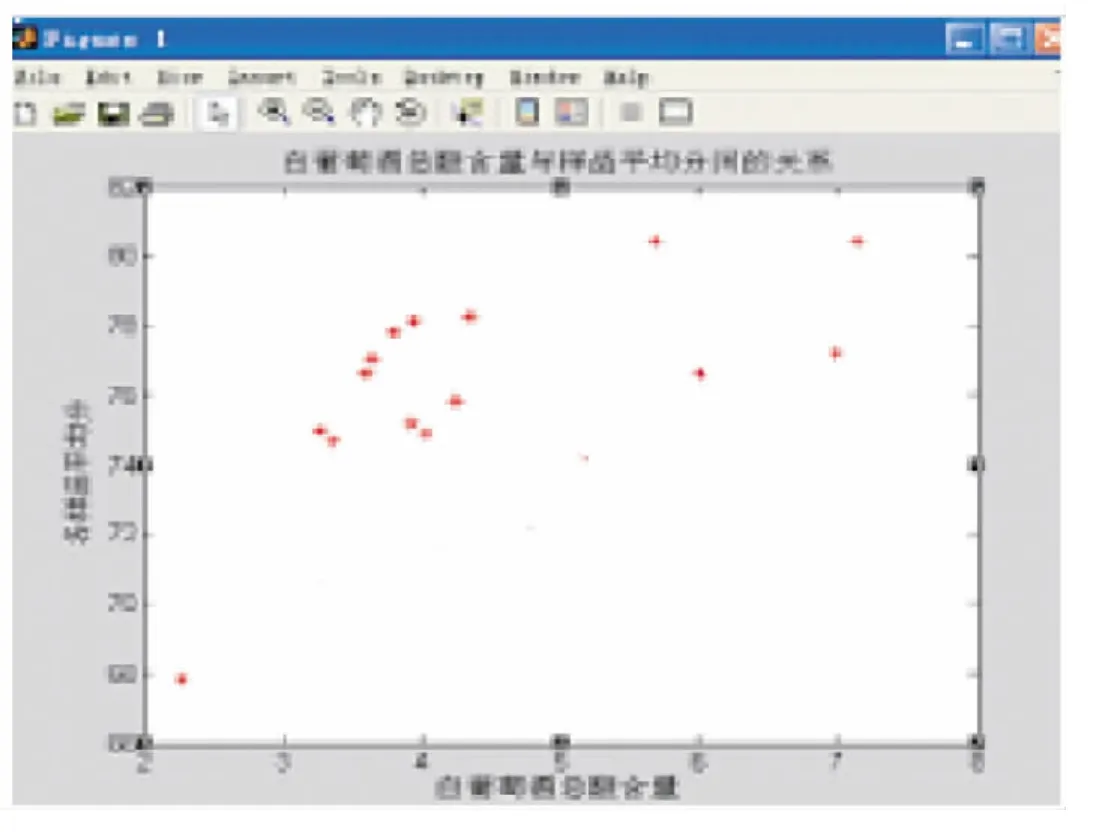
图8 白葡萄酒的总酸影响程度图
从而得到线性回归方程:
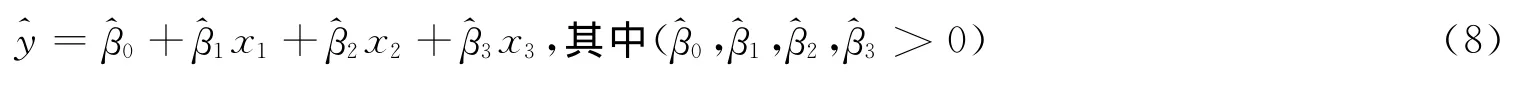
2.4 问题解决
通过对红、白葡萄酒酒样品的主要成分的分析,可以看到,不同等级间参数存在着差异。特别是总酚、单宁和总酸参数对不同等级呈极显著相关。数据分析表明总酚、单宁和总酸与葡萄酒的等级划分呈明显的正相关,即总酚、单宁和总酸含量越高,葡萄酒的等级越高。
3 结束语
在葡萄酒的感官评价中,由于品酒员间存在评价尺度、评价位置和评价方向等方面的差异,导致不同品酒员対同一酒样的评价差异很大。本文选取了10个专业品酒员分别对红葡萄酒27个酒样品和白葡萄酒28个酒样品进行品评打分,减少了误差,并选取了关键的理化指标参数进行分析,使问题得到了简化。
[1]马佩选.葡萄酒质量与检验[M].北京:中国计量出版社,2002:20-56.
[2]李记明,李华.葡萄酒成分分析与质量研究[J].食品与发酵工业,1994,(02):30-35.
[3]郭其昌,郭松泉.葡萄酒的质量等级法[J].中外葡萄与葡萄酒,1999,(04):64-67.
[4]赵宁,问亚琴,潘秋红.苯酚-硫酸法测定干红葡萄酒中的多糖含量[J].实验研究,2011,(04):9-17.
[5]刘丽媛,刘延琳,李华.葡萄酒香气化学研究进展[J].食品科学,2011,(05):310-316.
[6]李运,李记明,姜忠军.统计分析在葡萄酒质量评价中的应用[J].酿酒科技,2009,(04):79-82.
[7]张丽芝.贺兰山东麓红葡萄酒等级划分客观标准的初步研究[J].中国食物与营养,2012,18(03):29-32.
[8]卓金武.MATLAB在数学建模中的应用[M].北京:北京航空航天大学出版社,2011:3-52.
