分数跳-扩散下的增额寿险

刘 敏，薛 红，卢俊香

(西安工程大学理学院，西安710048)

保险商业是金融体系的重要组成部分，其中利率是保险精算学研究的重点.传统的精算理论假定利率是确定的.然而，在实际保险市场中，利率具有随机性.随着精算理论研究的不断深入，利率随机性的研究成果也在不断完善.1971年J·H·Polland首次把利率视为变量，对精算函数进行了研究;其后，Beekman 和 Fuelling［1-2］分别由 O-U 过程和Wiener过程对利息力建模，得到某些年金现值前二阶矩;De Schepper，Goovaerts［3-4］得到了利息力由Wiener过程建模的某些年金的矩母函数，分布函数与 Laplace变换;何文炯，蒋庆荣［5］对随机利率采用高斯过程建模，得到了一类即时给付的增额寿险给付现值的各阶矩，并在死亡均匀分布假设下得到了具体的简洁表达式;刘凌云，汪荣明［6］以即时给付的一类增额寿险为对象，考虑到突发时间对利率的影响，对随机利率采用Gauss过程和Poisson过程联合建模，给出即时给付的增额寿险给付现值的各阶矩，并在一些特殊条件下给出矩的简洁表达式;刘海芳，谭利，张立欣［7］考虑到不同性质的信息对利率的影响，对利率的随机性采用带Poisson跳的反射Brown运动建模，给出了一次缴清净保费、净均衡年保费和连续缴费方式下责任准备金的一般表达式.

考虑到利率的未来变化不仅与现在有关，而且与过去有关，用Brown运动和Poisson过程对利息力建立数学模型是不够完善的.而分数布朗运动具有长程依赖性恰好弥补了布朗运动的不足之处.吴晓蕊，薛红，李军［8］以综合人寿保险模型为研究对象，改进传统的常值利率的寿险模型，利用分数Brown运动和Poisson过程联合对利息力建立数学模型，获得了年金、终身寿险的精算现值公式.

本文采用分数Brown运动和Poisson过程联合对随机利率建模，对增额寿险理论中的保费、年金及责任准备金进行研究，并给出相应的表达式.

1 模型的建立

假定(x)表示年龄为x岁的人，T(x)表示(x)的剩余寿命，tPx表示(x)活到x+t岁的概率，μx+t表示(x)在x+t岁处的死亡力，则T(x)的概率密度函数为

现采用分数Brown运动和Poisson过程联合建模，设利息力积累函数为

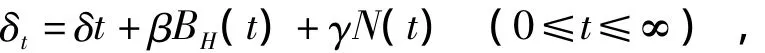
其中:δ为利息力常数，β 和 γ 为参数，{BH(t)，t≥0}为分数Brown运动，{N(t)，t≥0}为参数为λ的Poisson 过程，过程{BH(t)，t≥0}、{N(t)，t≥0}相互独立.

引理1［6］{N(t)，t(≥0}为参数为 λ 的 Poisson 过程，则{N(t)，t≥0}有分布

且

引理2［8］{BH(t)，t≥0}为分数 Brown 运动，则其概率密度函数为

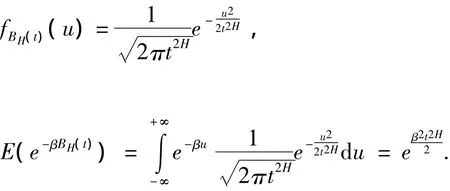
2 保费及年金的精算现值

考虑连续的n年期增额寿险，即保险期限为n年，若被保险人在n年末生存，则保险人不给付保险金;若被保险人在n年内死亡，则保险人立即给付相应的保险金.保险金为时间的函数，记为C(t)(t＞0)，此时增额寿险的给付现值函数可表示为

其中:V(t)=e-δt为贴现函数.

定理1 n年期增额寿险趸缴纯保费为

证明 根据精算现值的原理可知

特别的，当β=0时，可得常利率下的趸缴纯保费.

定理2若缴费期限为n年，当(x)生存时，每年连续支付数额为1的年金，记aT为n年定期生存年则n年定期生存年金的精算现值为

证明 根据精算现值的原理可知

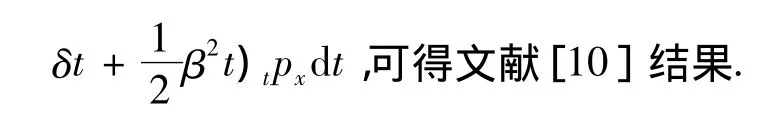
3 责任准备金

假设x+s岁的剩余寿命随机变量为ξ，则其概率密度分布为ξpx+sμx+s+ξ.当0 ≤s ＜ n时，保险公司在时刻s时的未来损失为

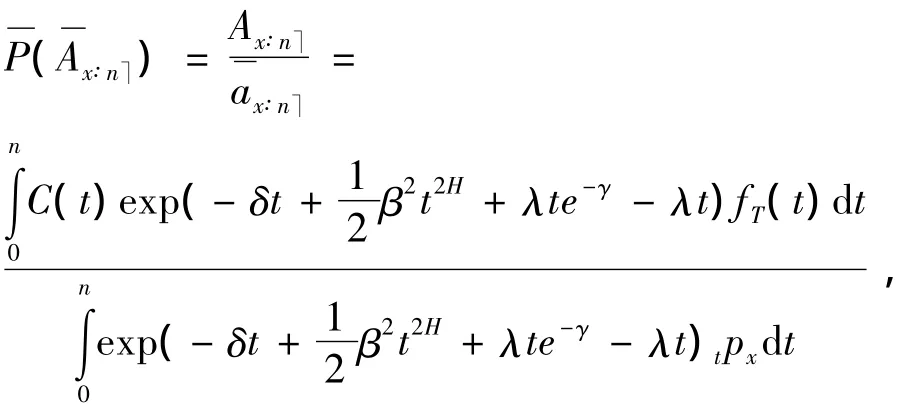
则s时刻的责任准备金为

特别的，当β=0，γ=0时，可得常利率下的责任准备金.

4 结 语

本文考虑了更为适合的随机利率模型，采用分数Brown 运动和Poisson 过程联合建模，相应的结论也更具有一般性，保险公司可以通过调节参数有效地控制利率的随机波动幅度，在一定程度上可以降低利率风险的影响. 当β = 0，γ = 0，λ = 0，那么δt = δt，即利息力为确定值. 本文中假设保险金C( t) ( t ＞ 0) 为时间的函数，其随着的变化而变化.当C( t) 取不同形式时，就得到不同寿险模型的相关结论.

参考文献:

［1］BEEKMAN J A，FUELING C P.Interest and mortality randomness in some annuities［J］.Insurance:Mathematics ＆Economics，1990，9:185-196.

［2］BEEKMAN J A，FUELING C P.Extra randomness in certain models［J］.Insurance:Mathematics ＆ Economics，1991，10:275-287.

［3］GOOVAERTS M，KASS R.Interest randomness in annuities certain［J］.Insurance:Mathematics ＆ Economics，1992，11:271-281.

［4］GOOVAERTS M.Some further results on annuities certain with random interest［J］.Insurance:Mathematics ＆Economics，1992，11:283-290.

［5］何文炯，蒋庆荣.随机利率下的增额寿险［J］.高校应用数学学报，1998，13A(2):145-152.

［6］刘凌云，汪荣明.一类随机利率下的增额寿险模型［J］.应用概率统计，2001，17(2):283-290.

［7］刘海芳，谭 利，张立欣.随机利率下的增额寿险模型［J］.数学理论与应用，2007，27(2):23-26.

［8］吴晓蕊，薛 红，李 军.分数跳-扩散下的综合人寿保险［J］.西安工程大学学报，2011，25(1):128.

［9］郭 欣.随机利率下的半连续型变额寿险模型［J］.四川理工学院学报，2012，25(4):86.

［10］叶迎春.连续时间随机利率条件下的寿险精算模型［J］.安徽商贸职业技术学院学报，2002，1(4):37.