一种基于Bessel函数的混沌神经网络

叶永刚，徐耀群

(哈尔滨商业大学基础科学学院，哈尔滨150028)

A·Potapove等指出，如果混沌神经元的激励函数是非单调函数，则单神经元能较快地执行混沌搜索[1].Shuai等提出有效的激励函数可以是不同的表现形式，并且应该表现出混沌行为[2].目前已有多种类型的混沌神经网络模型，并已用其成功地解决了组合优化问题[3－5]，但多数的混沌神经网络的神经元激励函数采用单调递增的函数[6－9].本文在Chen－Aihara暂态混沌神经网络的基础上提出了一种新的暂态混沌神经网络模型，在此模型中我们选择了具有较高的非线性度及较好的函数逼近能力的Bessel函数与Sigmoid函数的组合作为新的激励函数，构建了一种新的混沌神经元模型，该激励函数为非单调递增但总体上是递增的函数.利用混沌神经元的倒分叉图和最大Lyapunov指数时间演化图分析了新的暂态混沌神经网络的动力学特性.利用这种新的暂态混沌神经元模型我们建立了一种暂态神经网络，通过对所选择的非线性函数优化和10个城市的TSP问题的求解验证了此模型具有更快地找到全局最小的能力.

1 基于Bessel函数的混沌神经网络模型

1.1 Bessel函数

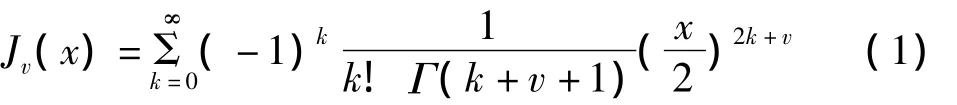
当v=－1，0，1时Bessel函数的图像如图1所示.

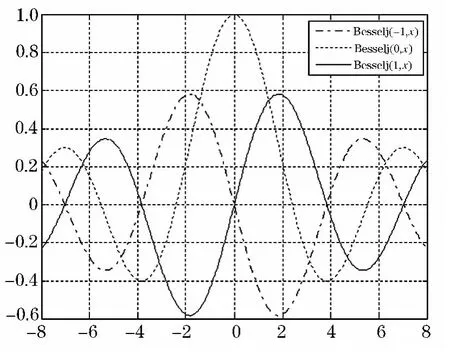
图1 v=－1，0，1时图像

由图1知，当v=－1，1时Bessel函数是奇函数，当v=0时Bessel函数是偶函数，且Bessel函数当x→∞时是震荡衰减的.

1.2 暂态混沌神经元模型

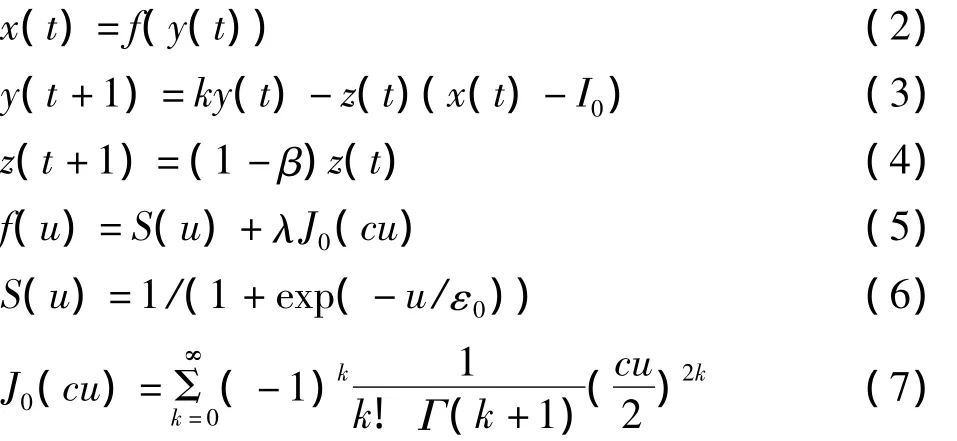
利用Bessel函数的特性，我们构造一种新暂态混沌的神经元模型，模型中激励函数为0阶的Bessel函数与Sigmoid函数的组合，取适当的参数后，激励函数为非单调递增但总体上是递增的函数，称此模型为Sigmoid－Bessel－Function模型，简称SBF模型.如下:其中:y(t)为神经元在t时刻的内部状态;x(t)为激励函数即神经元在的t时刻的输出;f(u)为该模型中激励函数;k的取值范围为0≤k≤1，表示神经元保留内部状态的能力;z(t)是自反馈连接项;I0为正参数;β是模拟退火参数;λ为组合系数;c为Bessel函数的伸缩系数;ε0是激励函数的陡度参数;

对于激励函数f(u)，若取参数λ=1/5，c=5，ε0=0.5时其图像如图2所示.

图2 激励函数在区间[－10，10]内的图像

为进一步分析此暂态混沌神经元的混沌动力学特性，分别取参数y(1)=0.825，k=1，z(1)=0.85，ε0=0.04，I0=0.45，β=0.002，λ=1/5，c=5时得神经元的倒分岔图和最大Lyapunov指数时间演化图如图3、4所示.

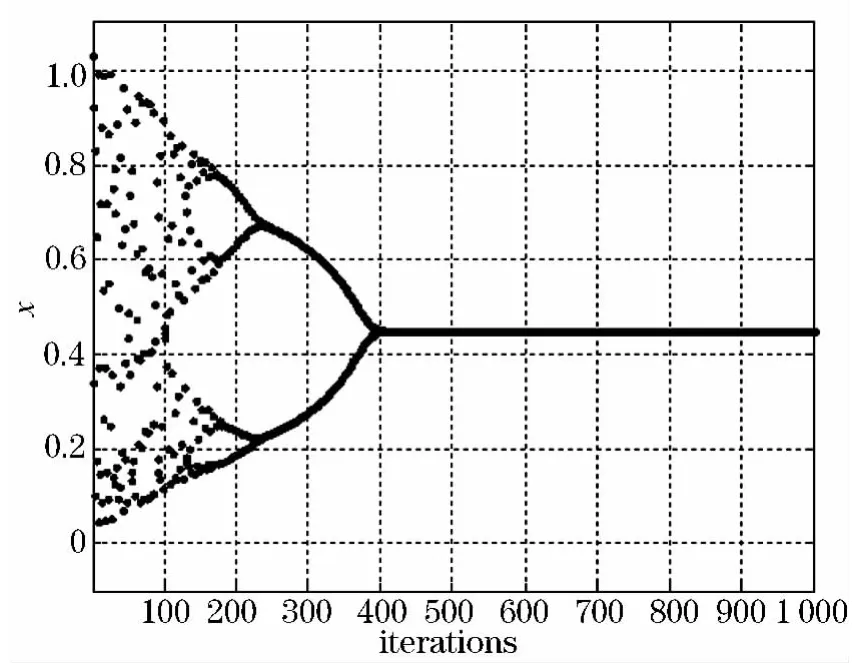
图3 SBF模型的暂态混沌神经元倒分岔图

由倒分岔图3可知，SBF模型的神经元的输出随着的不断衰减，经过一个混沌倒分岔过程逐渐稳定于平衡点.因此，网络求解优化问题时，有利于克服一般随机算法中以分布遍历性为搜索机制带来的局限性，使搜索具有内随机性和轨道遍历性，从而模型具有更强的避免收敛到局部极小的能力.

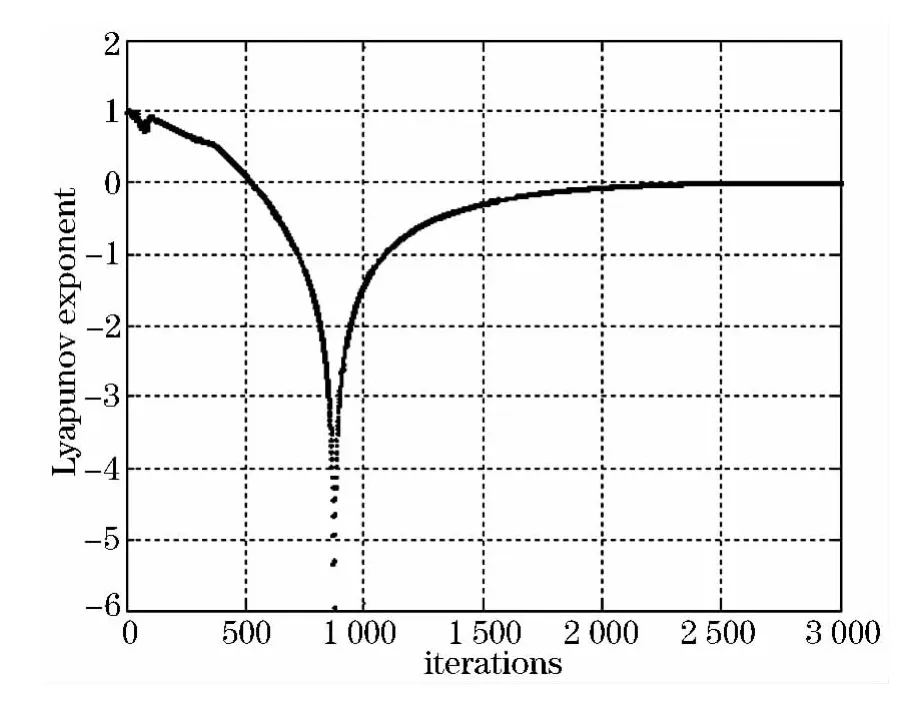
图4 神经元最大Lyapunov指数时间演化图

最大Lyapunov指数是经常用于定量描述混沌行为的量，当最大Lyapunov指数为正时，则神经元具有混沌动力学特性.由图4可知，神经元在开始时最大Lyapunov指数为正，网络处于混沌搜索状态，但随着自反馈连接项越来越小，最大Lyapunov指数由正逐渐变负，搜索逐渐失去混沌搜索能力，最终能使网络处于一种稳定的平衡状态.

综上可知，该神经元模型具有暂态混沌动力学行为，由于混沌搜索具有内随机性和轨道遍历性，故此神经元模型能使网络尽可能的避免收敛到局部最小值.

1.3 SBF暂态混沌神经网络模型

1.3.1 Chen－Aihara暂态混沌神经网络

Chen－Aihara神经网络模型如下[10]:

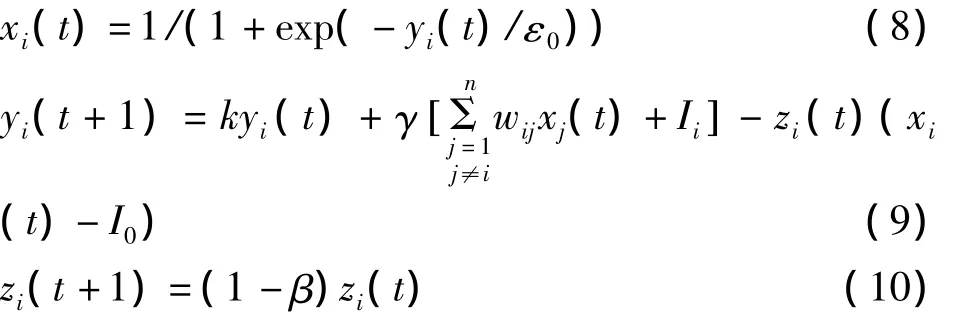
其中:xi(t)为激励函数即第i个神经元在t时刻的输出;其中yi(t)为第i个神经元在t时刻的内部状态;ε0是激励函数的陡度参数;k为神经隔膜的阻尼因子，0≤k≤1，代表网络记忆保留或遗忘内部状态的能力;γ为输入的正的尺度参数，代表着能量函数对混沌动力学特性的影响;wij为神经元j与i的连接权值，且有wij=wji，wii=0;Ii为神经元i的输入偏差;zi(t)为自反馈连接项，其值在模拟退火参数β的作用下不断减小，最终使网络处于一种稳定的平衡状态;I0为一正参数.

1.3.2 SBF暂态混沌神经网络

在Chen－Aihara神经网络模型基础上，利用构造的暂态混沌神经元模型，建立如下SBF暂态混沌神经网络模型:

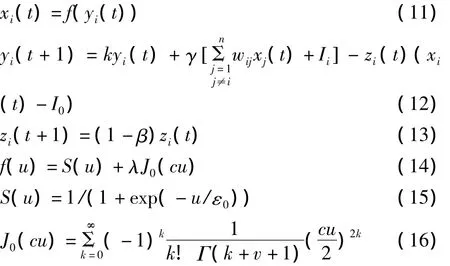
其中:xi(t)为激励函数即第i个神经元在t时刻的输出;其中yi(t)为第i个神经元在t时刻的内部状态;ε0是激励函数的陡度参数;k为神经隔膜的阻尼因子，0≤k≤1，代表网络记忆保留或遗忘内部状态的能力;γ为输入的正的尺度参数，代表着能量函数对混沌动力学特性的影响;wij为神经元j与i的连接权值，且有wij=wji，wii=0;Ii为神经元i的输入偏差;zi(t)为自反馈连接项，其值在模拟退火参数β的作用下不断减小，最终使网络处于一种稳定的平衡状态;I0为一正参数;λ为组合系数;c为Bessel函数的伸缩系数.

2 SBF暂态混沌神经网络模型在优化问题中的应用

2.1 SBF暂态混沌神经网络模型在函数优化中的应用选取以下优化函数[11]:

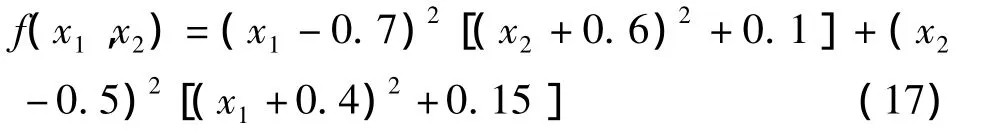
函数f的最小值为0，最小值点为(0.7，0.5);局部极小点为(0.6，0.4)与(0.6，0.5).

数据仿真中选取参数 ε0=0.4，k=1，γ=0.05，I0=0.45，β=0.002，y(1)=0.825，y(2)=0.825，z1(1)0.825，z1(1)=z2(1)=0.85时，SBF暂态混沌神经网络模型求解优化函数f的能量函数演化如图5所示.

图5 优化函数f的能量函数时间演化图

两个神经元输出值x1，x2的时间演化如图6所示.

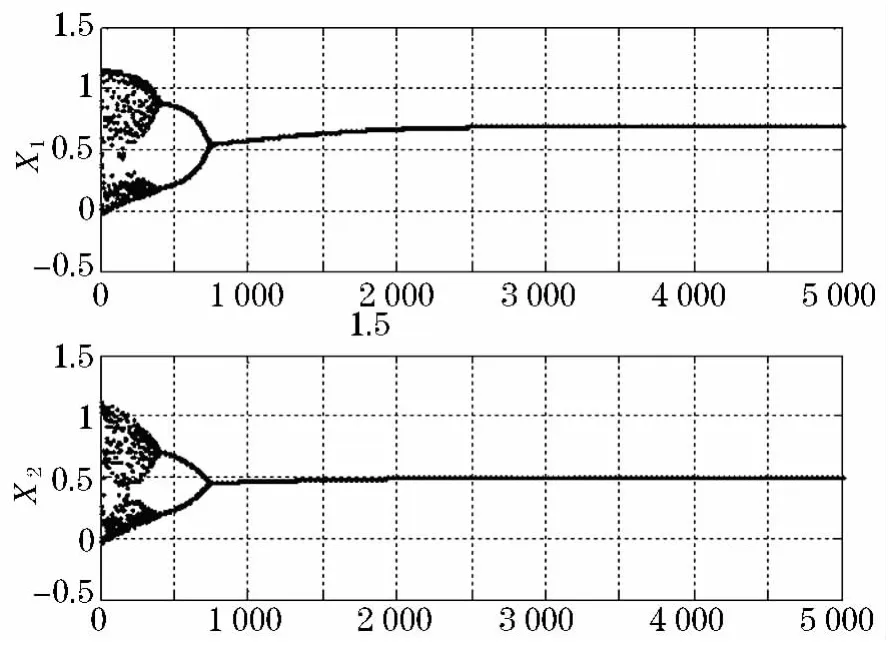
图6 两个神经元输出值x1，x2时间演化图

当网络运行5 000次时优化函数的能量函数值为7.293 240 7×10－9，此时x1=0.699 928，x2=0.499 986，搜索逐渐收敛到最小值.

2.2 SBF暂态混沌神经网络模型在TSP问题求解中的应用

TSP问题即旅行商最短路径问题是一个最具代表性的组合优化问题，找到该问题一个行之有效的解法是多年来许多学者努力的目标.TSP问题可以简述为:给定n个城市及任意两城市之间的距离，要求确定一条经过所有城市且每个城市仅经过一次的最短路线.本文将SBF暂态混沌神经网络模型应用于求解10个城市的TSP问题，仿真结果表明，此神经网络模型比Chen－Aihara神经网络模型具有更好的求解TSP问题的能力.

取能量函数为:

其中:dik为城市i到城市k的距离;xij表示以顺序j访问城市i，参数A=B，一个全局最小的能量值代表一条最短的有效路径.

选取归一化后的10个城市坐标，取值分别为:(0.4，0.443 9);(0.243 9，0.146 3);(0.170 7，0.229 3);(0.229 3，0.71 6);(0.517 1，0.941 4);(0.873 2，0.653 6);(0.687 8，0.521 9);(0.848 8，0.360 9);(0.668 3，0.253 6);(0.619 5，0.263 4)[5].该10个坐标的TSP问题满足条件的最短路径长度为2.677 6.

对于SBF暂态混沌神经网络模型，选取参数A=B=1、D=2、γ=0.25、k=1、I0=0.4、ε0=0.5、z(1)=0.8、β=0.002，每次运行程序时，在区间(－0.1，01)内200次随机赋予xij初值，程序共运行10次，其仿真结果如表1所示.

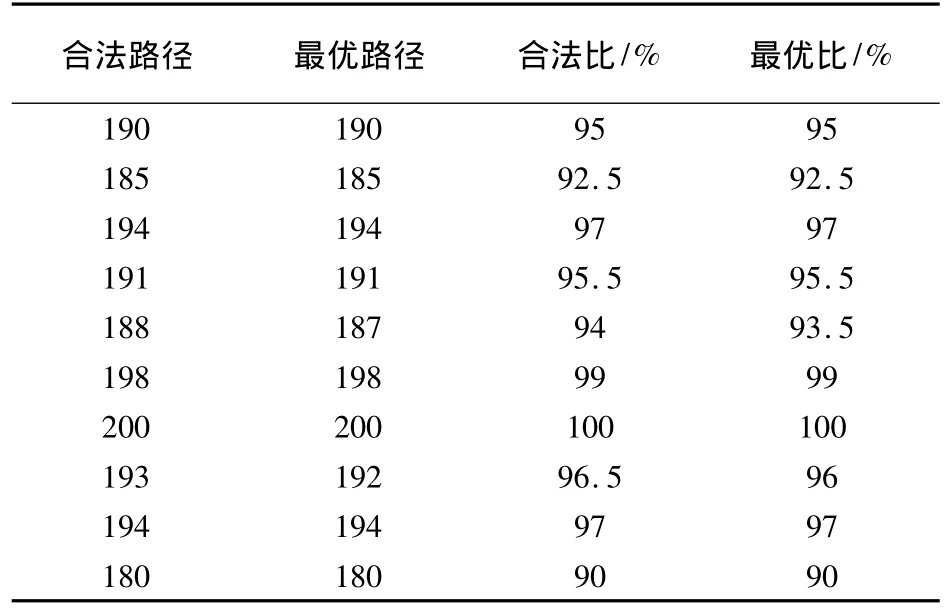
表1 SBF暂态混沌神经网络求解10城市旅行商问题的运行结果

由表1知，该网络求解10城市旅行商问题在上述参数情况下，其合法路径比最大为100%，合法路径比平均为95.7%，最优路径比最大为100%，最优路径比平均为95.6%，仿真结果表明，该神经网络具有很好的解决TSP问题的能力.仿真得最优路径如图7所示.

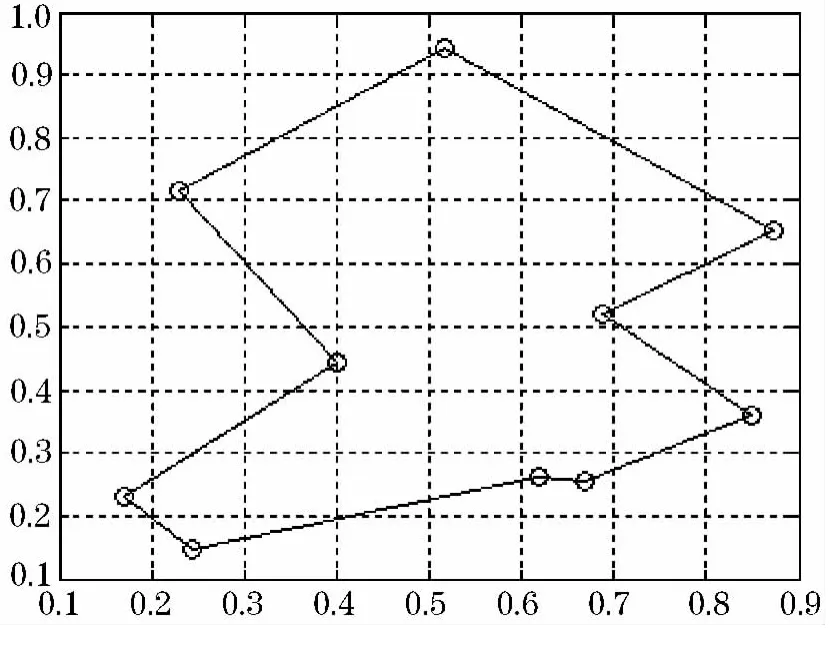
图7 10城市TSP归一化坐标的最短路径

3 结语

由于Bessel函数具有很高的非线性度及较好的函数逼近能力，本文把0阶Bessel函数引入到Chen－Aihara暂态混沌神经网络中的激励函数中，利用伸缩的0阶Bessel函数和Sigmoid函数组合作为新的激励函数，构建了一种新的暂态混沌神经网络.将此模型应用到求解优化函数及TSP问题的最优解中，仿真结果表明，此模型具有很强的求最优解能力.本文的模型中激励函数选取了固定的参数做了仿真实验，对于激励函数中参数的变化及高阶Bessel函数对模型的影响是我们要进一步研究的内容.

[1]POTAPOVE A，KALIM.Robust chaos in neural networks[J].Physics Letters－A，2000，277(6):310－322.

[2]SHUAIJW，CHEN Z X，LIU R T，et al.Self－evolution neuralmodel[J].Physics Letters－A，1996，221(5):311－316.

[3]CHEN L，AIHARA K.Chaotic simulated annealing by a neural network modelwith transient chaos[J].Neural Networks，1995，8(6):915－930.

[4]徐耀群，杨学岭，一类具有反三角函数自反馈的混沌神经网络及其应用[J].哈尔滨商业大学学报:自然科学版，2010，26(3):324－328.

[5]徐耀群，孙 明.Shannon小波混沌神经网络及其TSP(城市旅行商)问题的求解[J].控制理论与应用，2008，25(3):574－577.

[6]张 强，马润年，许 进.一种混沌神经网络模型及其在优化中的应用[J].系统工程与电子技术，2002，24(2):48－50.

[7]修春波，刘向东.一种新的混沌神经网络及其应用[J].电子学报，2005，33(5):868－870.

[8]XU Y Q，SUN M，SHEN JH.Shannon wavelet chaotic neural networks[J].Lecture Notes in Computer Science，2006，4247:244－251.

[9]贺昱曜，王力波.混沌神经网络及其在最优化问题中的应用[J].控制理论与应用，2000，17(6):847－852.

[10]徐耀群，孙 明.混沌神经网络及其应用[M].哈尔滨:黑龙江大学出版社，2012.

[11]王 涛，刘冬华.融合混沌和捕食搜索的混合粒子群算法[J].哈尔滨商业大学学报:自然科学版，2013，29(3):355－358.