基于局部规则的六足仿生机器人步态控制

尹晓琳，张 赫，赵 杰，刘玉斌，赵龙海

(哈尔滨工业大学机器人技术及系统国家重点实验室，哈尔滨150080)

轮式机器人和履带式机器人能够在平坦的地面上表现出良好的运动能力，但是在地球以及外部星球的大部分地面都是非平坦的、非结构化的地面，这时，轮式和履带式机器人的运动能力就不能很好地发挥，甚至有些地形都无法行走[1－3].足式机器人特别是六足机器人能够很好的克服轮式和履带式机器人的上述缺点，能够实现在复杂、非结构化的地面环境中实现稳定地行走.

由于六足机器人机械结构的复杂性，如何协调各腿之间的运动成为了一个难题，而步态的规划与控制则是其关键[4].步态可以实现六足机器人腿部的协调控制，根据一定的摆动——支撑顺序来控制机器人在工作环境中的行走.现在实现六足机器人步态控制的方法主要有基于中枢模式发生器原理(CPG)的方法和基于局部规则的方法[5－8]，前者环境适应能力差，而且实现步态直接的平滑转换比较困难，需要借助传感器修正CPG网络内部参数或外部行为来适应地形;而后者加入了传感器的反馈，根据腿部的传感器与环境之间的交互产生步态.本文设定了相应的局部步态规则，规划了适用于自由步态的足端轨迹，实现了步态的平滑转换.

1 本体结构

六足机器人的本体结构如图1所示，六足仿生机器人由躯干和六条完全相同腿组成，腿部采用高集成模块化的结构设计，由基节、股节和胫节组成，各个关节的结构也完全相同，保证了机器人良好的互换性.躯干里面集成有控制板，躯干－基节关节和基节－股节关节集成有一维力传感器，胫节集成有三维力传感器，可以随时监测足端以及各个关节的力以及力矩，实现机器人的实时控制.

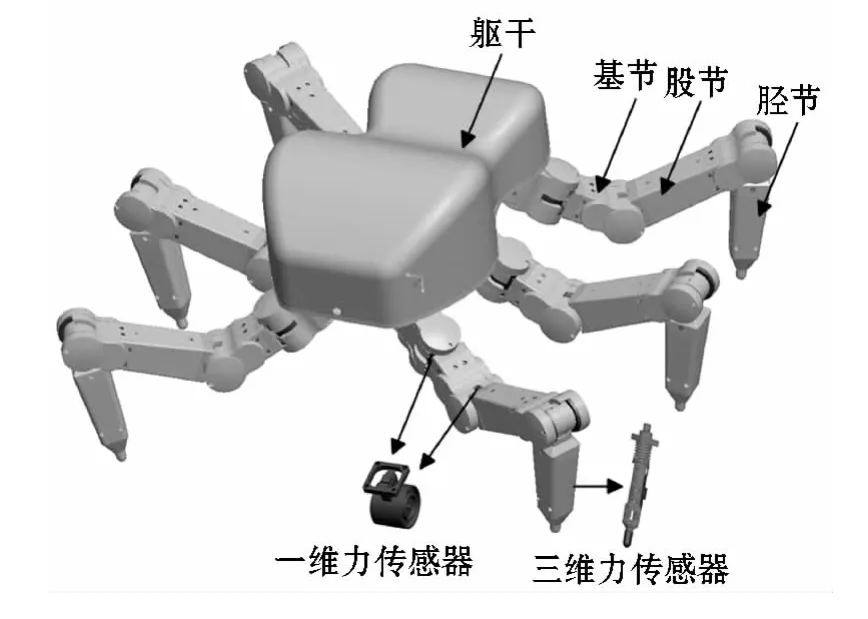
图1 六足机器人本体结构

单腿有躯干－基节关节(基关节)、基节－股节关节(髋关节)和股节－胫节关节(腕关节)三个关节组成，每个关节处有一个自由度，单腿具有三个自由度，建立D－H坐标系如图2所示，其中为基关节坐标系为髋关节坐标系为腕关节坐标系为足端坐标系，各坐标系的建立遵循杆件的坐标系建立规则，同时遵循右手螺旋定则.D－H参数如表1所示.

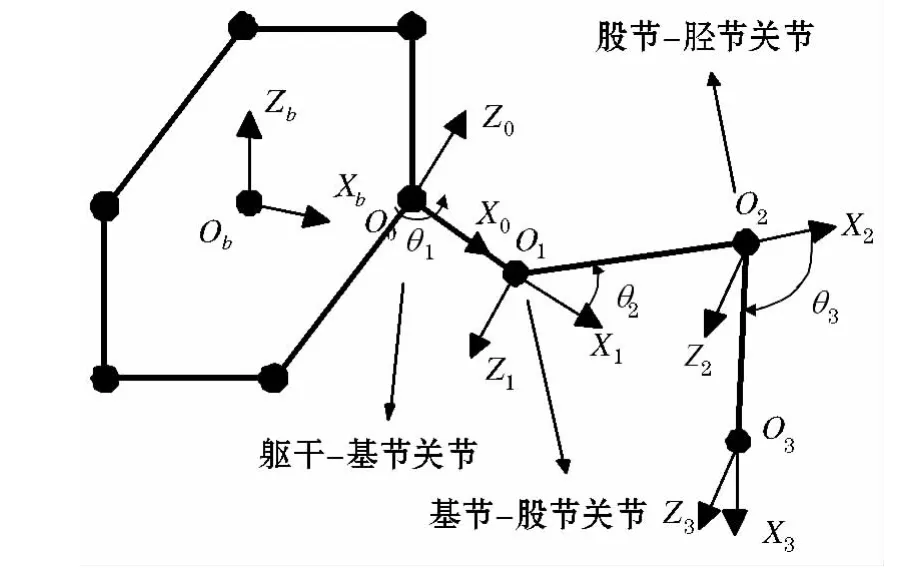
图2 运动学结构

足端点在躯干坐标系中的位置可以由坐标变换得到:

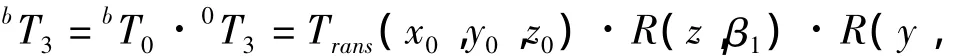
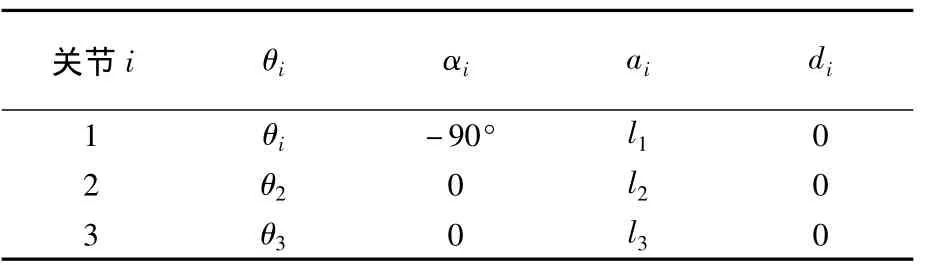
表1 腿部D－H参数表

其中前三项为躯干坐标系到躯干－基节关节坐标系的变换矩阵，其中为原点在躯干坐标系中的坐标为基节、股节和胫节的长度为相对于Ob－坐标变换的旋转角度.将参数带入式(1)中可以得到足端点在躯干坐标系中的坐标:

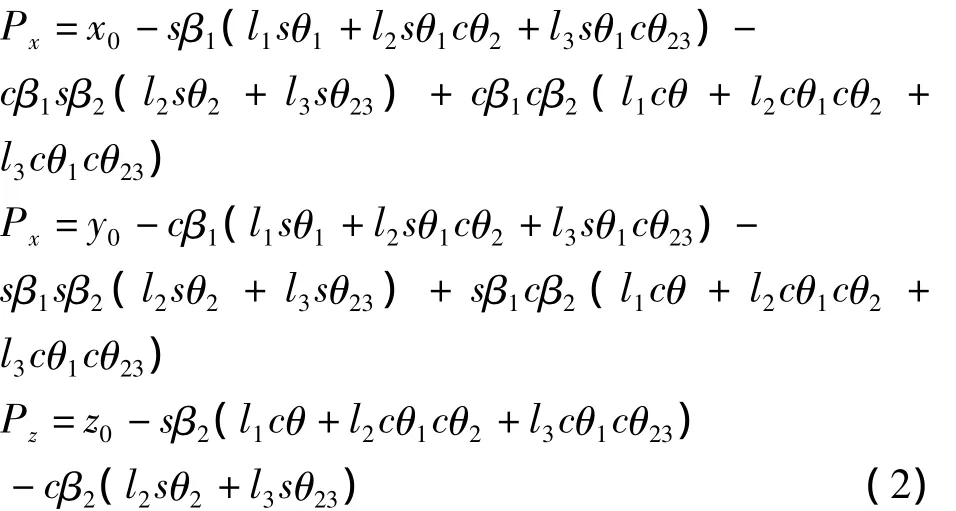
为了便于之后规划足端轨迹时确定前后极限位置的范围，对机器人足端工作空间进行了计算(如图3).

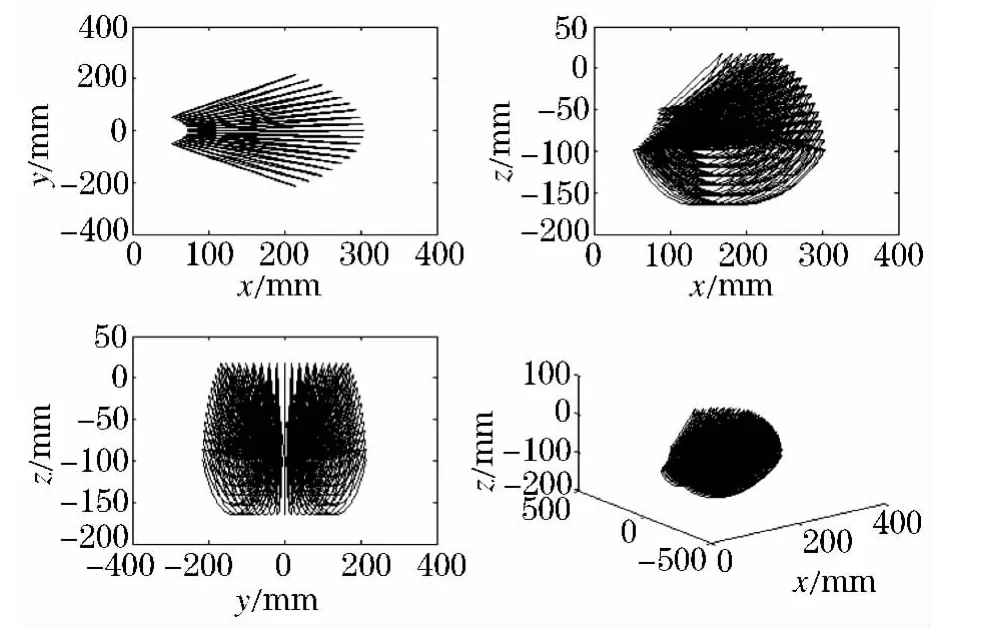
图3 足端工作空间

2 固化步态

2.1 步态参数

在行进过程中，六足仿生机器人的腿部运动是有规律的周期性变化，这一变化是由两个相互交替的变化实现的.一个是摆动相，此状态包括腿的抬起、前摆和下落并与地面接触;另一个是支撑相，是指腿部支撑地面，承受载荷，并向后摆动的过程.

六足仿生机器人的步态指的是六足机器人走路时所表现的姿态，它是建立在这种周期性变化的基础之上，通过改变摆动相和支撑相的时间比例及不同腿的相位差，形成六足仿生机器人的步态变化.

步行腿工作时状态发生变化的足端点位置定义为转变位置，也就是支撑相和摆动相发生交替的位置.步行腿工作时足端点所能达到最前以及最后的位置定义为极限位置和分别为支撑相和摆动相所持续的时间.β为占地系数，代表一个周期中支撑时间与总时间的比值，δ为稳定系数，描述步行中支撑腿的平均数目.如果一个单腿运动周期为T，机器人腿数为n，则:

定义机器人步长为s则机器人的平均移动速度可以表示为:

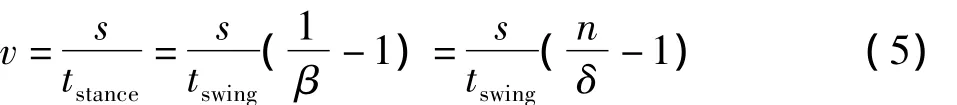
由于步长和摆动时间确定，所以将步行速度相同(占地系数/稳定系数相同)的各种步态，归为一类步态.假设s=100 mm，步行速度与δ足步态的关系曲线如图4所示.

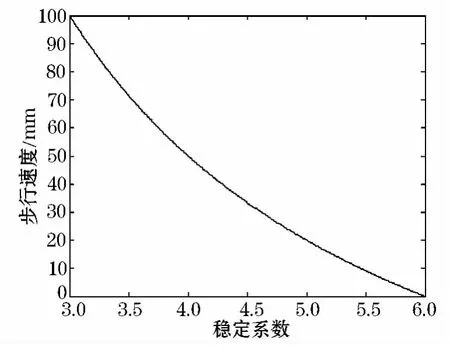
图4 速度与稳定系数关系

2.2 典型步态

2.2.1 三足步态

三足步态是六足机器人最常用的步态，也是速度最快、行走效率最高的一种步态.此处取为一组，0s时位于支撑相的零相位;L2、R1、R3为一组，0 s时位于摆动相的零相位，步态图如图5所示(黑色为支撑相).

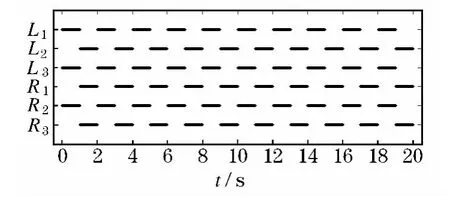
图5 三足步态步态图

2.2.2 四足步态

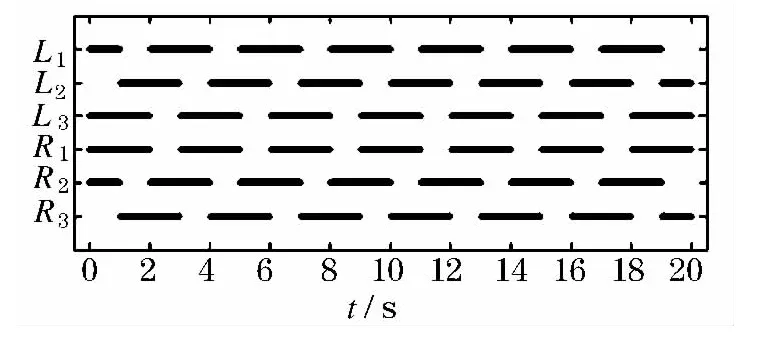
图6 四足步态步态图

2.2.3 五足步态

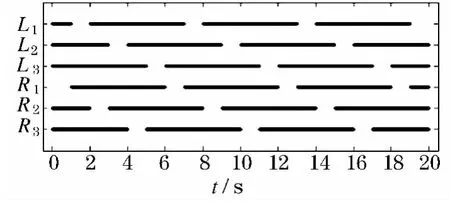
图7 五足步态步态图

3 局部规则及自由步态

3.1 基于自由步态的轨迹规划

在自由步态行走过程中六条腿的相位比较杂乱，各条腿进入支撑相也没有一个固定的时间，而机器人身体的速度只与支撑相的运动有关系，为了让身体有一个均匀的速度而非频繁地启停，规划了适合于自由步态的足端轨迹，如图8所示.图中A为前转换点，B为后转换点，C为后极限位置，D为最高点，E为前极限位置.其中A－B为支撑相，B－C－D－E－A为摆动相，图中虚线区域为缓冲区，目的是保证进入支撑相的点(A点)和出支撑相的点(B点)有一确定的速度，即使速度不为零的情况下也不至于产生比较大的力的波动，避免频繁启停.

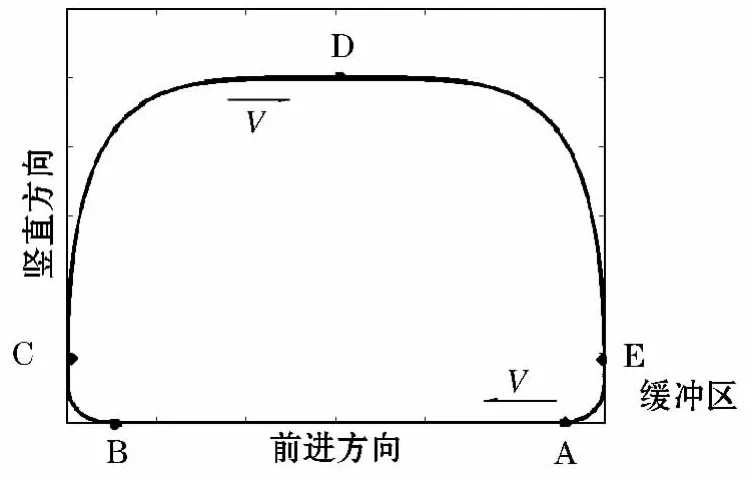
图8 足端轨迹规划

机器人足端在初始时刻与地面接触的位置可以由模型算得，在此位置做一与身体侧面平行的截面截足端工作空间如图9所示，其中F点为初始时刻足端点，将此区域简化为一矩形区域，即虚线框所包络的区域，所以可以取最大抬起高度为50 mm，步长为200 mm，这样即具有了一定的移动裕量又满足了一定的越障能力和移动速度.

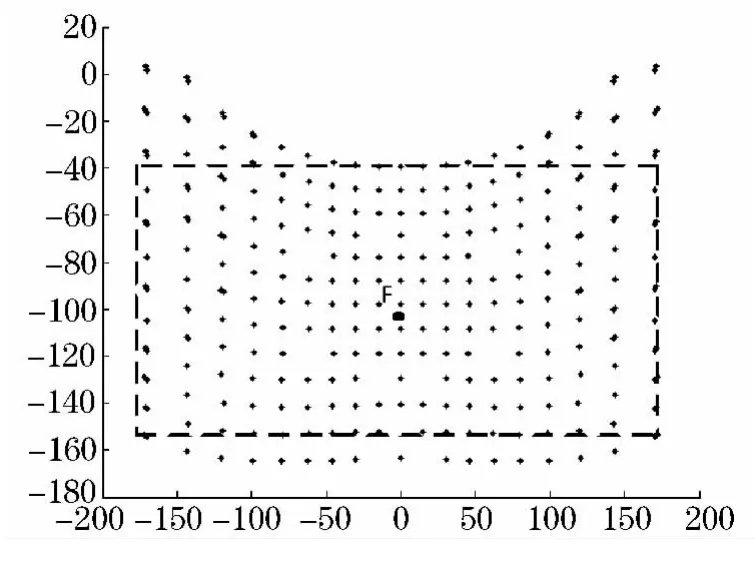
图9 足端工作空间截面

3.2 基于局部规则的自由步态

六足机器人的分布式控制控制，包括控制各自有着三个自由度的六条腿，即控制18个关节的协调运动.为了控制的简单化我们把控制器分为6个独立的子控制器，每个子控制器负责一条腿(L1、L2、L3、R1、R2、R3)的运动控制，如图10所示.每个子控制器又包含几个控制模块，包括目标控制模块、摆动控制模块、选择模块、高度控制模块和支撑控制模块.

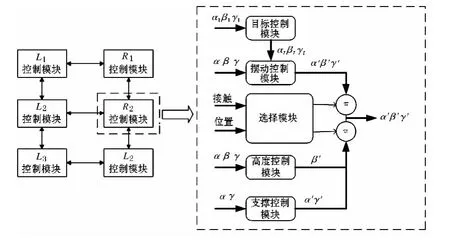
图10 六足机器人模块化控制

在“Walknet[9－10]”六足机器人控制结构所提出的三条规则的基础上做改进，改进后的腿间四条规则为:

规则1如果某条腿正在前摆，所有其相邻的腿必须处于支撑位置，将要进入摆动相的通过推迟后转变点来延长其处于摆动相的时间.

规则2支撑腿在到达后稳定位置即可开始进入摆动相，并强制其相邻的摆动腿进入支撑相.此处要规定一个摆动优先级:L3＞R3，L3＞L2，R3＞R2，L2＞R2，L2＞L1，R2＞R1，L1＞R1，即从后向前，从左向右.

规则3刚进入支撑相的腿，通过提前相邻腿的后转换点来激励其前摆，此规则的优先级为:L3＞L2＞L1，R3＞R2＞R1，即由后向前.

规则4足端点按照3.1中规划的足端轨迹进行摆动和支撑，某条腿进入支撑相时应满足速度和机器人躯干的速度相同.

此四条规则通过同时修正前转变位置和后转变位置来协调机器人腿间的运动，相比之前只延迟后转变位置的方法调整时间短、效率高.同时在后两个规则中加入了腿的摆动/支撑优先级，使协调腿间运动的计算更具有针对性，这样，在选择控制模块中选用前三条规则进行各腿相位的调整，然后其他模块采用离线规划的形式，调用之前规划好的适合于自由步态的足端轨迹就能控制机器人自主的行走.流程图如图11所示.

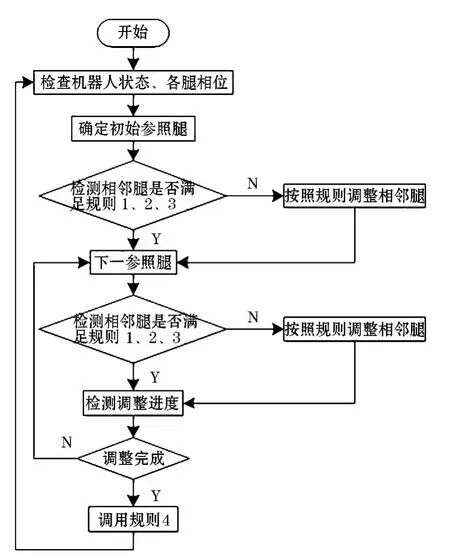
图11 基于局部规则的控制流程图

假设摆动相时间为1 s，支撑相时间分别是1、2、5 s，在t=0时刻六条腿同时开始支撑(均处于支撑相的零相位)，加入上述四条规则之前和加入之后的步态图如图12所示.

由图可以看出调整前的三种步态是没有办法行走的，因为在同一时刻有相邻的腿同时抬起，机器人失去了稳定.而加入局部规则算法之后生成的步态图是可以行走的.

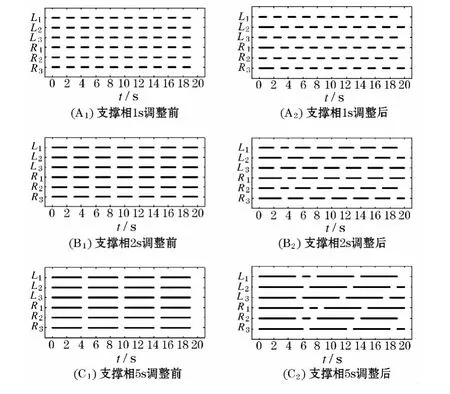
图12 调整前后比较

4 仿真分析

定义摆动相时间为1 s，支撑相时间为1 s，机器人速度为0.1 m/s，给定一个杂乱的初始相位，使L1、L2、L3、R1、R2、R3分别位于其支撑相的0、2π/5、4π/5、6π/5、8π/5、0相位.设定最大抬起高度为50 mm.步态调整图如图13所示，仿真动画截图如图14所示，各个关节角位置和角速度与步态图的对比如图15～17所示(实线:角位置，虚线:角速度)，机器人速度如图18所示.

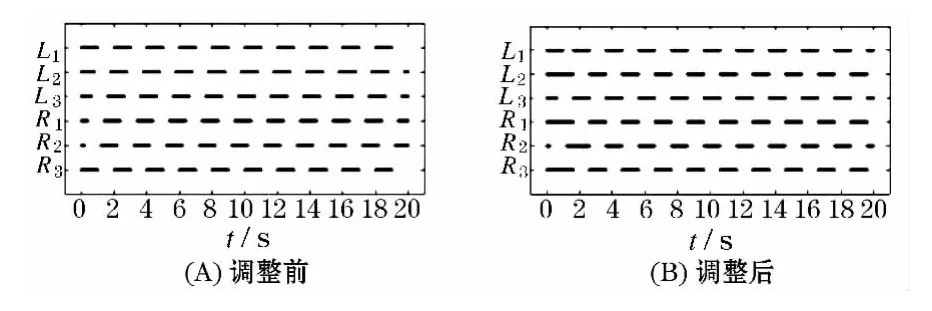
图13 不同初始相位步态调整图

由仿真结果可以看出3 s左右的时候，步态已经调整到正常的三足步态模式，之后稳定地行走，由此证明了基于局部规则的算法的可实现性，此基于局部规则自由步态是正确的，可执行的.并且能够保证比较稳定的躯干的速度和平滑的关节曲线.

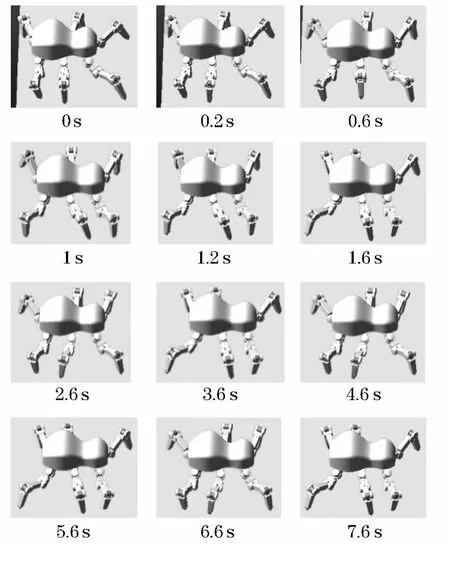
图14 自由步态仿真截图

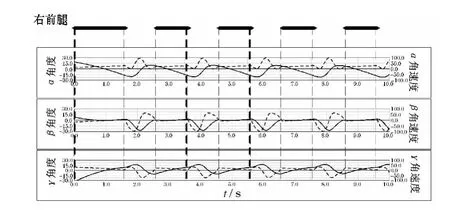
图15 右前腿关节角度与角速度

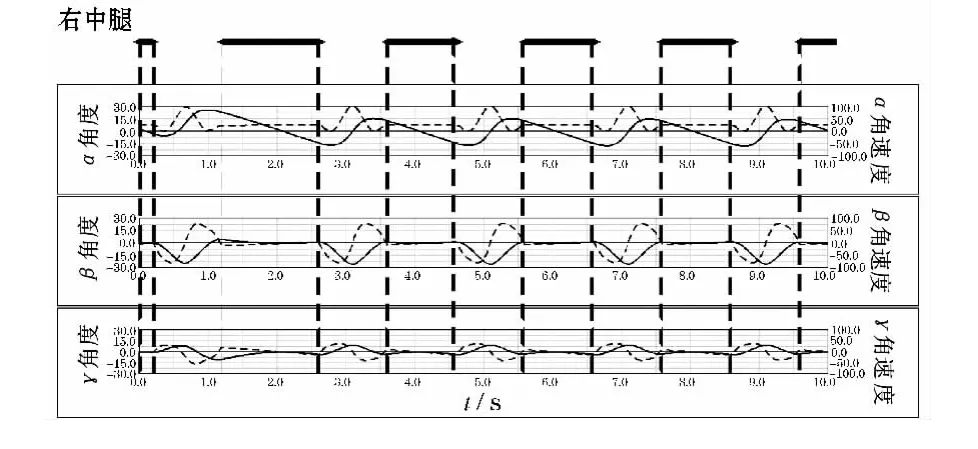
图16 右中腿关节角度与角速度

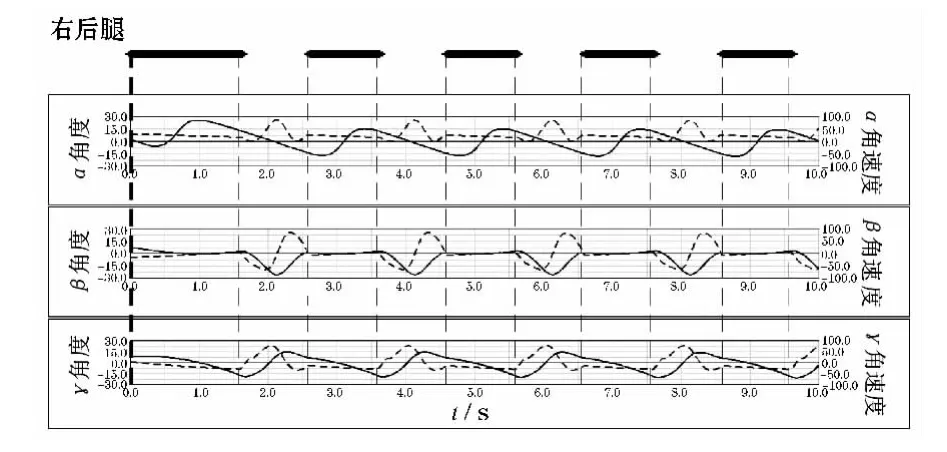
图17 右后腿关节角度与角速度

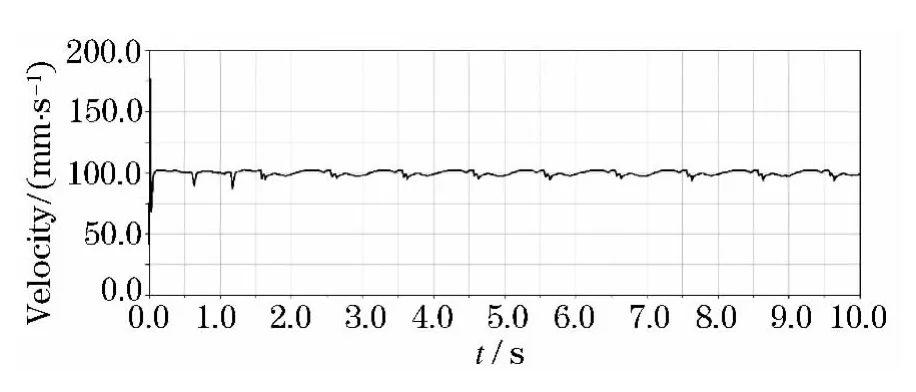
图18 躯干速度

5 结语

本文在结合六足仿生机器人运动学的基础上对步态的概念以及运动速度与步态参数直接的关系进行了分析计算，提出了三种基本的固化步态;在之前“Walknet”控制结构上做了改进，提出了四条协调腿部运动的规则以及基于局部规则的一种足端轨迹规划方法，实现了机器人腿间相序的调整以及自主的行走，同时能够稳定机器人的步行速度;仿真实验结果表明，提出的四条规则和足端轨迹规划方法是正确可行的，为之后进一步研究打下了基础.

[1]陈 甫，臧希喆，闫继宏，等.适合航行的六足仿生机器人Spider的研制[J].吉林大学学报，2011，41(3):765－770.

[2]刘海清，刘玉斌，张 赫，等.仿生六足机器人基于足力分布的位姿调整策略[J].哈尔滨商业大学学报:自然科学版，2012，28(5):541－545.

[3]VLADAREANUl L，TONT G，ION I，et al.Walking Robots Dynamic Control Systems on an Uneven Terrain[J].Advances in Electrical and Computer Engineering，2010，10(2):145－152.

[4]徐鲤鸿，党 皓，陈伟海，等.一种六足步行机器人的自由步态算法[J].机器人技术，2008，24(22):200－202.

[5]SCHILLING M，SCHNEIDER A，CRUSE H，et al.Local controlmechanisms in six－legged walking[C]//The IEEE/RSJInternational Conference on Intelligent Robots and Systems，Nice，France，2008:2655－2660.

[6]SCHILLING M，CRUSE H，ARENA P.Hexapod Walking:an expansion to Walknet dealing with leg amputations and force oscillations[J].Biological Cybernetics，2007，96:323－340.

[7]KINDERMANN T.Behavior and Adaptability of a Six－Legged Walking System with Highly Distributed Control[J].Adaptive Behavior，2002，9(1):16－41.

[8]CRUSEH，BARTLING C，KINDERMANN T.High－pass filtered positivefeedback for decentralized control of cooperation[J].Advances in Arti cial Life，1995，929:668－678.

[9]CRUSE H，KINDERMANN T，SCHUMM M，etal.Walkneta biologically inspired network to control six－legged walking[J].Neural Netw，1998，11(7－8):1435－1447.

[10]方婉霏，潘 博，付宜利.微创手术机器人被动式关节设计和优化[J].哈尔滨商业大学学报:自然科学版，2013，29(3):309－313.