纵向地震作用下大跨三塔悬索桥伸缩缝处双边碰撞效应研究

邓育林，雷 凡，何雄君

(武汉理工大学 交通学院，武汉 430063)

地震灾害经验表明，相邻桥跨间的碰撞效应是导致桥梁破坏的重要原因。诸如，我国1976年唐山大地震，对滦河大桥落梁破坏的解释都不同程度的提到碰撞效应的影响。1989年美国Loma Prieta地震中，由于低估了相邻桥跨间的相对位移且预留的支承面太窄，致使旧金山-奥克兰海湾大桥引桥发生落梁。1995年日本阪神地震中，主跨252m的西宫港大桥第一跨引桥落梁的主要原因是主、引桥间的相对位移过大而产生的碰撞。我国2008年的汶川大地震中，桥梁结构相邻梁体伸缩缝处的碰撞现象也很普遍，其中，庙子坪大桥一跨引桥在伸缩缝处坠落就可能是由于主、引桥梁体伸缩缝处的碰撞引起的。

自上世纪90年代开始，国外许多学者就对桥梁伸缩缝间的碰撞现象进行了深入研究［1-5］，而我国对该领域的研究尚处于起步阶段，有关桥梁结构地震碰撞问题研究的文献还不多。并且研究大多针对中小跨径梁式桥或者是连续钢构桥［6-7］，而针对大跨斜拉或者悬索桥主、引桥伸缩缝处相邻梁体的碰撞效应研究较少［8-9］。为此，本文以一座大跨三塔悬索桥为研究对象，建立复杂的桥梁结构空间动力分析模型，采用非线性动力时程分析法，详细分析大跨三塔悬索桥伸缩缝处主、引桥相邻梁体间的双边碰撞对桥梁结构地震反应的影响规律，揭示大跨桥梁主、引桥结构振动周期比与碰撞效应的内在联系，为大跨桥梁抗震设计提供理论参考。

1 计算模型

某一大跨三塔悬索桥，主跨1080m，主缆分跨为390 m+1080 m+1080 m+390m，边塔塔高178.0m，为混凝土塔，中塔塔高192.0m，为变截面钢塔，纵向为人字型，横桥向为门式框架结构，中塔下横梁与主梁间设置纵向设弹性索，如图1所示。

图1 大跨悬索桥布置图Fig.1 Arrangement of long-span suspension bridge

分析时，两侧各取一联引桥，为4×70m等墩高连续梁桥，居中设置一固定墩，其余各墩为活动墩，墩高从20m～50m变化，桥墩为薄壁空心墩，外围尺寸为6.5 ×4.2m，墩高为 30m 及以下时，壁厚为 50cm，墩高大于30m时，壁厚为70cm。

采用弹塑性纤维梁(Fiber)单元模拟引桥桥墩、主塔墩，将纤维分别赋予混凝土和钢筋的应力-应变关系，其中，混凝土采用Kent-Park模型，钢筋采用Giuffré-Menegotto-Pinto模型模拟。为模拟伸缩缝处主、引桥相邻梁体的碰撞现象，采用图3所示的接触单元模拟两侧伸缩缝，其非线性力-位移的关系如下:

式中:gd为地震作用下相邻梁体的相对位移;gp为伸缩缝初始间隙;kk为接触刚度，可取较短梁体的轴向刚度;ck为阻尼系数，用来反映碰撞过程中的能量损失。

图2 伸缩缝模型Fig.2 Expansion joints model

根据能量守恒定律，可推导出阻尼系数ck与碰撞过程中恢复系数e之间的关系如下:

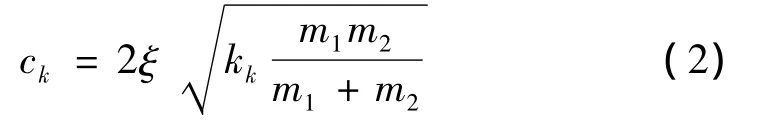
式中，m1和m2分别为两碰撞刚体的质量。

2 双边碰撞对结构地震反应的影响

本文主要研究大跨悬索桥伸缩缝处双边碰撞效应对结构地震响应的影响。考虑到结构的对称性，分析时，北侧引桥墩高变化范围为20～35 m，南侧引桥墩高变化范围为20～50 m，接触单元初始间隙取不考虑碰撞效应时主、引桥最大相对位移的1/2，恢复系数e取1.0，即不考虑碰撞过程中的能量耗散。为了将双边碰撞效应与单边碰撞效应进行对比，还进行了单边碰撞效应的分析，即忽略北引桥的影响，只考虑主桥与南引桥间的碰撞效应。

选取表1所示的9条地震波，所选地震波的特征周期覆盖范围较宽，在0.26～0.88 s之间变化，这样分析结果具有一定的普遍性和代表性。假定桥址位于地震高烈度区，将每条地震波的加速度峰值调整到0.4 g，沿结构纵桥向输入，地震动输入采用一致激励，不考虑地震动的空间效应。分析采用专用程序Opensees［10］进行。

表1 选取的地震波Tab.1 Selected free-field ground motions

由于相邻桥跨周期比是影响地震碰撞效应的关键因素，因此，为分析方便，将主桥位移控制振型周期记为T0，北侧引桥基本周期记为T1，南侧引桥基本周期记为T2，笔者在文献［8］中分析了主桥T0与引桥周期T1，T2关系，结果表明当引桥墩高为25 m时，主桥T0与引桥周期T1，T2最为接近。

2.1 碰撞引起的最大撞击力

图3～图4分别给出考虑双边碰撞效应，南北两侧伸缩缝处最大撞击力随南侧引桥墩高的变化曲线，取9条地震波的平均值。

从图3可以看出:当北引桥墩高为25m时，北引桥T1与主桥T0最为接近，北引桥与主桥梁体不同向振动程度最轻，从而北侧最大撞击力响应最小;随着北引桥墩高的增大或者减小，北引桥与主桥梁体不同向振动程度逐渐增大，北侧最大撞击力响应也相应逐渐增大;当主桥T0与北引桥T1(墩高为20～25m)接近时，南引桥T2的变化对北端碰撞力峰值影响不大，而当北引桥大于主桥T0(墩高为30～35m)时，北端碰撞力峰值随南引桥T2的增大先减小而后增大，其中，当两侧引桥T1与T2相同时，北侧最大撞击力响应最小。

从图4可以看出:南侧最大撞击力响应随南引桥T2的变化趋势基本一致，当南引桥墩高为25m时，南引桥T2与主桥T0最为接近，南引桥与主桥梁体不同向振动程度最轻，从而南侧最大撞击力响应达到最小;当南北两侧引桥墩高都大于25m时，就南侧最大撞击力响应而言，单边碰撞总体上大于双边碰撞，而当北引桥墩高小于25m时，双边碰撞总体上大于单边碰撞。

2.2 碰撞对引桥地震内力的影响

分析结果表明碰撞可能会增大引桥桥墩的地震内力响应，而对主桥的地震内力响应影响较小，因此以下仅讨论双边碰撞效应对引桥桥墩的影响。

图5～图6分别给出考虑双边碰撞效应，南北两侧引桥固定墩墩底曲率峰值响应比(φp/φn)随南侧引桥墩高的变化曲线，取9条地震波的平均值，其中，下标p和n分别表示考虑与不考虑碰撞效应时的地震响应。

从图5可以看出:当北引桥墩高为20 m时，主桥T0大于北引桥T1，双边碰撞使北引桥固定墩墩底曲率峰值响应有所减小，且南引桥墩高的变化对其影响很小;而当北引桥墩高大于25 m时，主桥T0小于北引桥T1时，双边碰撞使北引桥固定墩墩底曲率峰值响应有所增大，若南引桥墩高一定时，其增大程度随北引桥墩高的增大而增大。

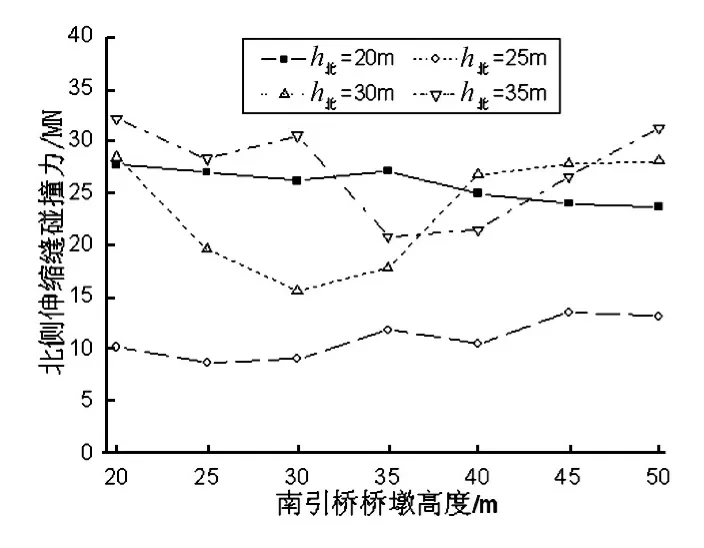
图3 北侧碰撞力峰值Fig.3 Peak pounding force of the North

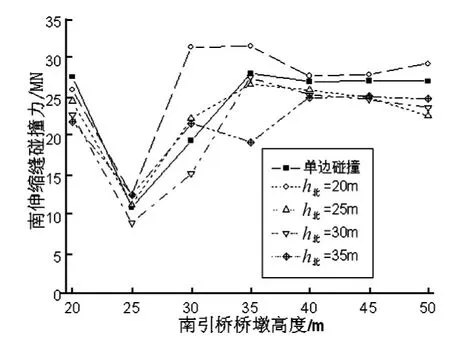
图4 碰撞力峰值Fig.4 Peak pounding force of the South

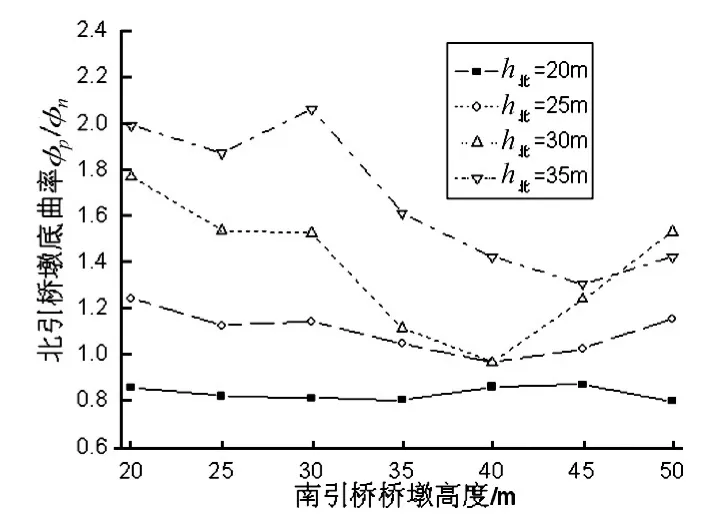
图5 北引桥墩底曲率峰值比Fig.5.Mean amplification and variation in maximum curvature demand of the North pier

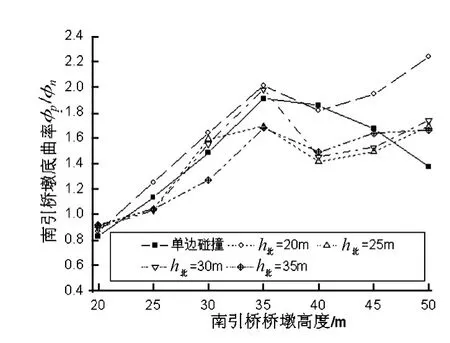
图6 南侧引桥墩底曲率峰值比Fig.6 Mean amplification and variation in maximum curvature demand of the south pier

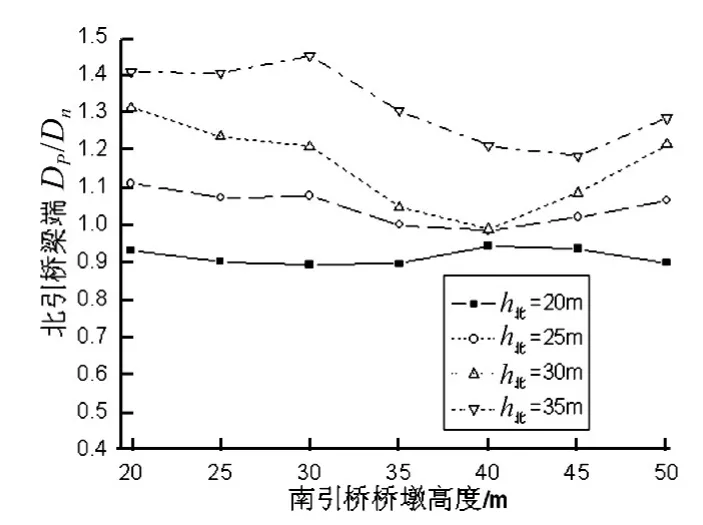
图7 北引桥梁端位移峰值比Fig.7 Peak displacement amplification of the beam end of the North approach-span

图8 南引桥梁端位移峰值比Fig.8 Peak displacement amplification of the beam end of the Sorth approach-span

从图6可以看出:当南引桥墩高为20 m时，主桥T0大于南引桥T2，双边碰撞使南引桥固定墩墩底曲率峰值响应轻微减小;而当南引桥墩高大于25 m时，主桥T0小于南引桥T2时，双边碰撞使南引桥固定墩墩底曲率峰值响应增大，但随着南引桥墩高变化有所起伏，总体上随着南引桥T2增大而增大，且随着南引桥T2与北引桥T1差异的增大而增大，如当北引桥墩高为20 m，南引桥墩高为50 m，双边碰撞使南引桥固定墩墩底曲率峰值响应增大达到120%;此外，对于南引桥固定墩墩底曲率峰值响应的影响，当北引桥T1小于或者接近主桥T0时，双边碰撞效应总体大于单边碰撞效应，而当北引桥T1大于主桥T0时，单边碰撞效应总体上大于双边碰撞效应。

3.3 碰撞对引桥梁端位移的影响

图7～图8分别给出考虑双边碰撞效应，南北两侧引桥梁端位移响应峰值比(Dp/Dn)随南侧引桥墩高的变化曲线，取9条地震波的平均值，其中，下标p和n分别表示考虑与不考虑碰撞效应时的地震响应。

从图7可以看出:当北引桥墩高为20 m时，主桥T0大于北引桥T1，双边碰撞使北引桥梁端位移响应轻微减小，且南引桥墩高的变化对其影响很小，而当北引桥墩高大于25 m时，主桥T0小于北引桥T1时，双边碰撞使北引桥梁端位移响应增大，当南引桥墩高一定时，其增大程度随着北引桥T1增大而增大;

从图8可以看出:当南引桥墩高为20 m时，主桥T0大于南引桥T2，双边碰撞使南引桥梁端位移响应减小，而当南引桥墩高大于25 m时，主桥T0小于南引桥T2时，双边碰撞使南引桥梁端位移响应增大，其增大效应随着南引桥T2增大而增大，且当南引桥T2与北引桥T1差异最大时达到峰值，如当北引桥墩高为20 m，南引桥墩高为50 m，双边碰撞使南引桥梁端位移响应增大达到110%;此外，对于南引桥梁端位移响应的影响，当北引桥T1小于或者接近主桥T0时，双边碰撞效应总体大于单边碰撞效应，而当北引桥T1大于主桥T0时，单边碰撞效应总体上大于双边碰撞效应。

3.4 碰撞对相对位移的影响

图9～图10分别给出考虑双边碰撞效应，南北两侧主、引桥间相对位移响应峰值比(ΔDp/ΔDn)随南侧引桥墩高的变化曲线，取9条地震波的平均值，其中，下标p和n分别表示考虑与不考虑碰撞效应时的地震响应。

图9 北端主引桥相对位移峰值比Fig.9 Peak relative displacement a mplification of the North

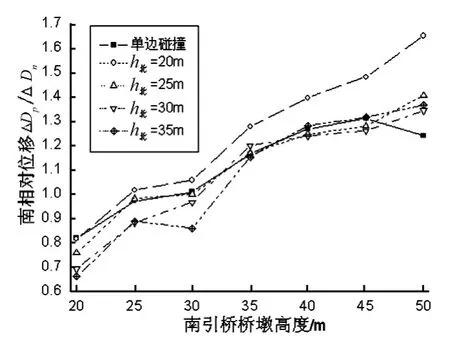
图10 南端主引桥相对位移峰值比Fig.10 Peak relative displacement amplification of the South

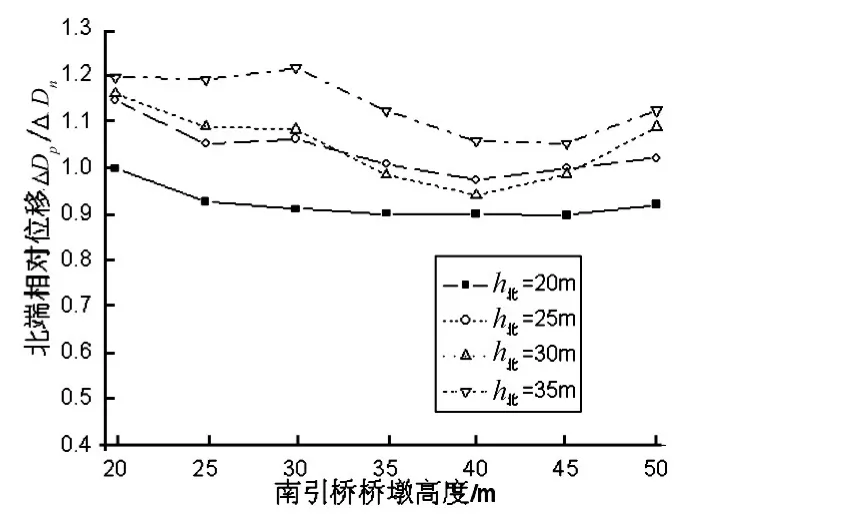
图11 北引桥梁体搭接长度峰值比Fig.11 Peak hinge seat width amplification of the beam end of the North approach-span

从图9可以看出:当北引桥墩高为20 m时，主桥T0大于北引桥T1，双边碰撞使北端主、引桥间相对位移响应减小，而当北引桥墩高大于25 m时，主桥T0小于北引桥T1时，双边碰撞可能会使北端主、引桥间相对位移响应增大，当南引桥墩高一定时，其增大程度随着北引桥T1增大而增大;

从图10可以看出:当南引桥墩高小于30 m时，南引桥T2小于或者接近主桥T0，双边碰撞使南端主、引桥间相对位移响应减小，而当南引桥墩高大于30 m时，南引桥T2大于主桥T0，双边碰撞使南端主、引桥间相对位移响应增大，且当南引桥T2与北引桥T1差异最大时达到峰值，如当北引桥墩高为20 m，南引桥墩高为50 m，双边碰撞使南端主、引桥间相对位移响应增大达到65%;此外，对于南端主、引桥间相对位移响应的影响，当北引桥T1小于或者接近主桥T0时，双边碰撞效应总体大于单边碰撞效应，而当北引桥T1大于主桥T0时，单边碰撞效应总体上大于双边碰撞效应。

图11～图12分别给出考虑双边碰撞效应，南北两侧引桥梁体搭接长度响应峰值比(ΔDp/ΔDn)随南侧引桥墩高的变化曲线，取9条地震波的平均值，其中，下标p和n分别表示考虑与不考虑碰撞效应时的地震响应。

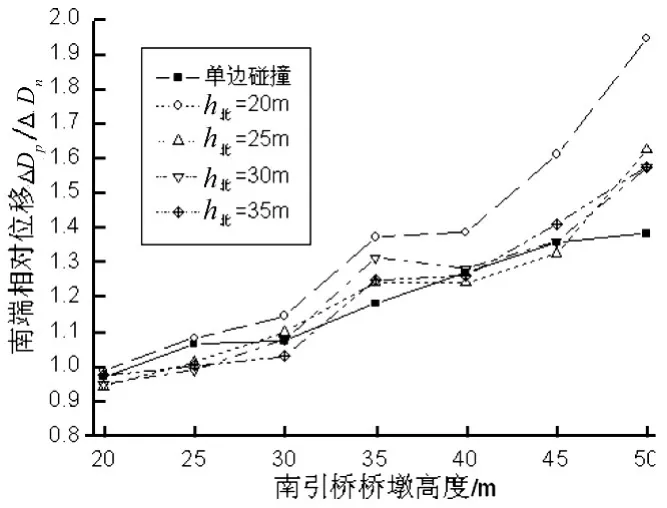
图12 南引桥梁体搭接长度峰值比Fig.12 Peak hinge seat width amplification of the beam end of the South approach-span

从图11可以看出:当北引桥墩高为20 m时，主桥T0大于北引桥T1，双边碰撞使北引桥梁体搭接长度响应轻微减小，且随南引桥墩高变化很小;而当北引桥墩高大于25 m时，主桥T0小于北引桥T1时，双边碰撞使北引桥梁体搭接长度响应增大，当南引桥墩高一定时，其增大程度随着北引桥墩高的增大而增大。

从图12可以看出:当南引桥墩高为20 m时，主桥T0大于南引桥T2，双边碰撞使南引桥梁体搭接长度响应减小;而当南引桥墩高大于25 m时，主桥T0小于南引桥T2时，双边碰撞使南引桥梁体搭接长度响应增大，其增大效应随着南引桥T2增大而增大，且当南引桥T2与北引桥T1差异最大时达到峰值，如当北引桥墩高为20 m，南引桥墩高为50 m，双边碰撞使南引桥梁体搭接长度响应增大近100%;此外，对于南引桥梁体搭接长度响应的影响，当北引桥T1小于或者接近主桥T0时，双边碰撞效应总体大于单边碰撞效应，而当北引桥T1大于主桥T0时，单边碰撞效应总体上大于双边碰撞效应。

3 结论

通过以上分析可以得出以下结论:

(1)当一侧引桥周期小于或者接近主桥周期，而另一侧引桥周期显著大于主桥周期时，双边碰撞使长周期侧的引桥墩底地震内力、梁端位移、梁体搭接长度以及主、引桥间相对位移响应增大，而使短周期侧的引桥梁端位移、主引桥相对位移及引桥梁体搭接长度响应轻微减小。

(2)当一侧引桥周期小于或者接近主桥周期，而另一侧引桥周期显著大于主桥周期时，双边碰撞效应总体大于单边碰撞效应，而当两侧引桥周期都大于主桥周期时，单边碰撞效应总体上大于双边碰撞效应。

(3)在实际工程抗震设计中，如果一端引桥周期与主桥周期相差不大，而另一侧引桥周期与主桥周期相差较大时，应需重视双边碰撞效应对长周期侧地震响应的不利影响。

［1］Malhotra P K.Dynamics of seismic pounding at expansion joints ofconcrete bridges［J］.JournalofEngineering Mechanics/July，1998:794-802.

［2］ Chouw N，Hao H.Study of SSI and non-uniform ground motion effect on pounding between bridge girders［J］.Soil Dynamics and Earthquake Engineering，2005，25:717 728.

［3］ Jankowski R，Wilde K，Fujino Y.Reduction of pounding effects in elevated bridges during earthquakes［J］.Earthquake Engineering and Structural Dynamics，2000，29:195-212.

［4］ Chau K T，Wei X X，Guo X，et al.Experimental and theoretical simulations of seismic poundings between two adjacentstructures［J］. Earthquake Engineering and Structural Dynamics，2003;32:537-554.

［5］ Ruangrassamee A， KawashimaK. Relativedisplacement response spectra with pounding effect［J］. Earthquake Engineering and Structural Dynamics，2001，30:1511-1538.

［6］王军文，李建中，范立础.非规则梁桥伸缩缝处的碰撞对地震反应的影响［J］.土木工程学报，2006，30(1):54-59.

WANG Jun-wen，LI Jian-zhong，FAN Li-chu.Effect of pounding at expansion joints on seismic response of irregular girder bridges［J］.China Civil Englneerlng Journal，2006，30(1):54-59.

［7］王军文，李建中，范立础.连续梁桥纵向地震碰撞反应参数研究［J］.中国公路学报，2005，18(4):42-47.

WANG Jun-wen，LI Jian-zhong，FAN Li-chu.Parametric study of longitudinal seismic pounding response for continuous girder bridges［J］.China Journal of Highway and Transport，2005，18(4):42-47.

［8］邓育林，彭天波，李建中.大跨多塔悬索桥纵向地震碰撞反应参数研究［J］.振动与冲击，2011，30(4):152-157.

DENG Yu-lin，PENG Tian-bo，LI Jian-zhong.Parametric study of longitudinal seismic pounding response for long-span multi-tower suspension bridges［J］.Journal of Vibration and Shock，2011，30(4):152-157.

［9］邓育林，彭天波，李建中.强震作用下大跨斜拉桥伸缩缝处的碰撞效应影响研究［J］.振动与冲击，2011，30(6):26-30.

DENG Yu-lin，PENG Tian-bo，LI Jian-zhong.Effect of pounding at expansion joints on seismic response of long-span cable-stayed bridge under strong earthquakes［J］.Journal of Vibration and Shock，2011，30(6):26-30.

［10］OpenSeesCommand Language Manual［M］. Pacific EarthquakeEngineering Research Center，University of California，Berkeley，OpenSees version 2.2.1.，2011.