受撞桥梁结构撞击力仿真分析研究
2015-06-01刘小燕朱洲洲姜太新陈偲鹏
刘小燕, 朱洲洲, 姜太新, 陈偲鹏
(长沙理工大学 土木与建筑学院, 长沙 410015)
受撞桥梁结构撞击力仿真分析研究
刘小燕, 朱洲洲, 姜太新, 陈偲鹏
(长沙理工大学 土木与建筑学院, 长沙 410015)
桥梁上部结构受到超高车辆撞击时会产生很大的损伤. 为了掌握结构的损伤情况, 需要确定撞击力的大小.本文基于仿真模型对超高车辆撞击桥梁上部结构的撞击力进行研究. 采用Ansys/Ls-dyna软件建立有限元模型, 分析不同车重、速度下的撞击力大小和变化规律. 通过多参数曲线拟合获取受撞桥梁结构撞击力的计算公式, 并与国内外相关文献资料的结果进行比较, 验证了拟合公式的可靠性, 从而为相关工程设计及加固提供参考.
超高车辆; 撞击; 桥梁结构; 仿真模型; 撞击力
引言
近几年来, 由于经济的快速发展, 公路上超高超大型车辆的数量越来越多, 而以往建设的一些跨线桥梁桥下净空高度满足不了桥下所过车辆的需求, 导致超高车辆撞击桥梁上部结构的事故时有发生. 据北京交通部门近几年的统计数据显示, 北京市50%的桥梁上部结构曾遭超高车辆的撞击, 由此损坏的桥梁占已损坏桥梁的20%以上[1]. 桥梁受到车辆的撞击时, 会给桥梁带来严重损伤, 轻则中断交通, 重则引起桥梁的倒塌以及其他车辆追尾侧翻, 造成重大的人员伤亡及巨大的经济损失. 为了减少这一损失, 一方面,在进行桥梁设计时, 应充分考虑桥下净空的要求, 留有足够的桥下净空; 另一方面, 需要计算撞击对桥梁结构产生的影响, 从而采取正确的加固对策. 在进行桥梁结构撞击计算时, 撞击力大小的确定是至关重要的问题. 我国桥梁设计通用规范[2]参考国外规范, 简单规定“撞击力在车辆行驶方向取1000kN, 垂直方向取500kN”. 这样规定, 虽然计算简单方便, 但与实际并不相符: 简单规定一个值, 既没有考虑车辆重量大小的影响, 也没有顾及撞击时车速情况. 陆新征[3]等人对影响撞击力的因素进行了研究, 得出车重、车速等对撞击力的影响较大, 规范关于撞击力的规定与实际有较大出入. 在进行车桥碰撞研究时各国学者沿用船桥碰撞计算思路, 将其引入车桥碰撞的计算中, 主要的计算公式有Woisin公式[4]、欧洲统一规范规定的船桥碰撞计算公式[5]、美国《公路桥梁设计规范》[6]中的船桥撞击力计算公式、我国《公路桥涵设计通用规范》[2]及《铁路桥涵设计基本规范》[7]中的关于船桥撞击力计算的公式等, 上述计算公式有些是基于试验数据和经验得出来的, 只适用于船桥碰撞撞击力的计算, 对于车桥碰撞撞击力的计算问题并没有见报道. 本文研究超高车辆撞击桥梁上部结构的撞击力问题, 采用Ansys软件的Ansys/Ls-dyna建立仿真模型, 考虑车辆质量及车速等因素对桥梁上部结构撞击影响, 应用多参数曲线拟合方法给出撞击力的计算公式, 为相关工程及桥梁加固设计提供参考.
1 有限元模型
车辆撞击桥梁上部结构是非常复杂的动力非线性问题, 涉及大量的结构非线性、材料非线性、接触非线性以及动力效应, 通常采用非线性有限元技术来研究. 文[3]提出了用Ansys/Ls-dyna能够较好的对车辆撞击桥梁这一非线性问题进行分析, 本文根据这一思路开展计算, 首先建立车桥模型, 然后计算车桥撞击荷载, 通过大量计算比较, 提出撞击力计算公式.
1.1 车桥模型
采用文[8]提出的标准双轴卡车有限元模型, 如图1所示. 以某受撞16m跨径简支T梁桥为例, 横截面由5片T梁组成, 如图2所示, 主梁混凝土采用C30, 普通钢筋为HRB335.
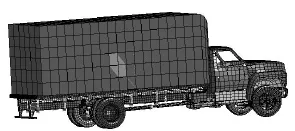
图1 车辆有限元模型示意图
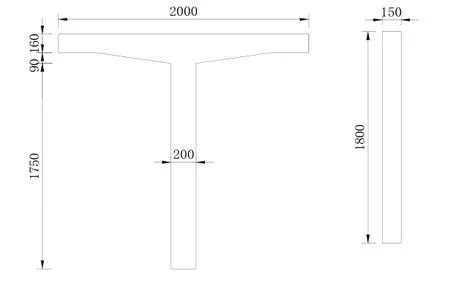
图2 T梁横截面及横隔梁示意图(mm)
混凝土采用Solid164单元进行模拟, 材料本构关系采用HJC(Holmquist-Johnson-Cook)模型, 普通钢筋采用Link180单元进行模拟, 钢筋采用Cowper-Symonds本构模型, 桥梁模型如图3所示, 车辆撞击桥梁上部结构模型如图4所示.

图3 桥梁模型示意图
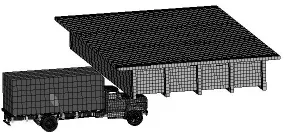
图4 车桥碰撞模型示意图
1.2 模型检验
模型的正确性在车辆撞击计算分析中起着决定性的作用, 整个撞击过程中主要能量有动能、内能、接触能以及沙漏能等. 为了保证结果的可靠性, 总能量必须守恒, 且沙漏能以及接触能不超过总能量的10%[9], 此处通过车桥撞击过程中能量的转化情况及与已有研究结果进行比较来检验模型的正确性. 对上面建立的车桥碰撞模型的计算可得到, 车辆碰撞桥梁过程中能量的相互转化关系图如图5所示, 8t车辆以10m/s的速度撞击桥梁时的撞击力时程图如图6所示.

图5 能量转化情况示意图
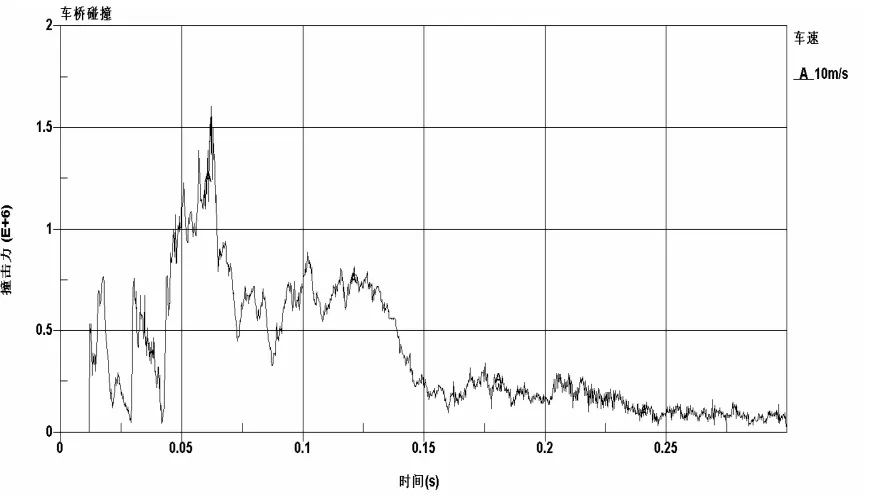
图6 撞击力时程图
由图可知, 沙漏能和接触能都很小, 沙漏能及接触能都控制在10%以内, 且8t重车辆以10m/s的速度撞击桥梁结构时的最大值撞击力为1.608×106N, 与文献[3]中的结果相当.
2 车桥撞击力
车辆撞击桥梁上部结构是一动态过程, 撞击力是一条时程曲线, 在桥梁设计中一般是将其等效成静力荷载[10], 用撞击力的最大值或平均值计算, 本文主要研究撞击力最大值Pmax及撞击力平均值Paver. 撞击力平均值即撞击过程中总的冲量与撞击时间的比值. 在车辆撞击桥梁上部结构工程中, 诸多因素都会对其产生影响, 如: 车速、车重、桥长、车型、支座以及车辆撞击桥梁位置等. 由文献[11]可知车辆的质量、速度对撞击力影响很大, 因此本文主要研究车辆质量、速度对撞击力大小的影响, 并采用多参数曲线拟合的方法得出撞击力计算公式.
2.1 撞击力计算的多参数方法
假设最大撞击力及平均撞击力可表示为车重与车速函数关系的积[9]:

其中R、R′为常数;M为车辆的质量, 单位为吨(t);F1、F2为分别表示撞击力关于车重、车速的关系式;V为车辆撞击桥梁时的速度, 单位为m/s.
由仿真模型计算出的撞击力时程关系曲线, 进行曲线拟合即可得到撞击力计算公式.
2.2 车重对撞击荷载的影响在车桥碰撞过程中, 车辆质量是影响撞击力大小最重要的因素, 在研究车重对撞击力大小的影响时, 考虑工程实际, 选用几种常见车重及车速进行计算, 具体见表1.

表1 各影响因素的取值
由表1可知, 共有50种工况. 由于文章篇幅有限, 此处只给出部分不同车重以V= 10m/s的速度撞击桥梁时的撞击力时程图. 不同车重撞击桥梁上部结构撞击力时程图如图7所示.
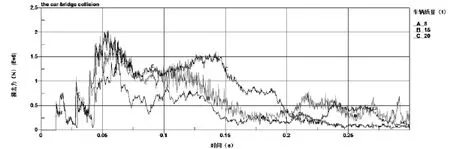
图7 不同车重撞击力时程图
由图7可知, 车辆撞击桥梁时, 在大约0.01s时, 桥梁受到一个很大的突加荷载的作用, 但此时的撞击力远小于撞击力最大值, 撞击力最大值大约在0.05s达到, 随后撞击力快速减小, 从不同车重撞击力时程图可以看出, 车重为20t、15t、8t时撞击力最大值分别为2.039×106N、1.827×106N、1.608×106N, 经比较可知, 撞击力最大值随车重的增加而增大.
将上述50个工况按质量不同速度相同的工况归为一组, 共有10组. 每组撞击力均以30t车重时的撞击力为基准进行归一化, 得到撞击力峰值比率及平均撞击力比率. 在研究车重对撞击力的影响规律时, 为了控制车速的影响, 将车重相同速度不同所对应的撞击力比率求平均值, 最后对平均值进行拟合. 由于文章篇幅有限不再给出具体计算数值, 拟合曲线及方程如图8和图9所示.
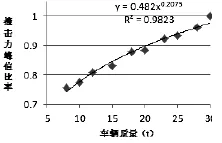
图8 撞击力最大值拟合关系式图
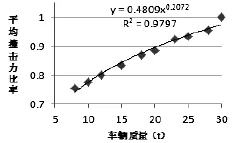
图9 撞击力平均值拟合关系图
由图8和图9可知, 车桥撞击时, 撞击力与车重成非线性关系, 由相关性系数可以看出, 撞击力大小与车重的关系比较符合幂函数的关系. 经拟合后, 撞击力最大值和撞击力平均值与车重的关系式如下:

2.3 车速对撞击荷载的影响
车辆速度与车重一样, 对撞击力大小的影响很大, 研究车速对撞击力影响的工况与表1一致, 此处给出8t重车辆以不同速度撞击桥梁跨中时的撞击力时程图, 具体大小如图10所示.
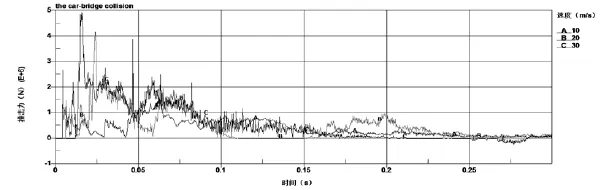
图10 不同速度撞击力时程图
从图10可以看出, 当车辆以10m/s、20m/s、30m/s撞击桥梁时, 撞击力最大值分别为1.608×106N、3.873×106N、4.938×106N, 可以看出, 撞击力最大值与车速呈正相关关系, 并且车速越大撞击力增加的速度越快, 峰值越早达到.
同样, 按照处理不同车重撞击力数值的方法对不同车速撞击力大小按30m/s的速度进行归一化处理,得到不同速度下撞击力比率平均值, 经过拟合即可得到撞击力与速度之间的关系式如图11和图12所示.
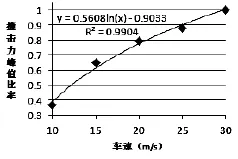
图11 撞击力最大值拟合关系式图
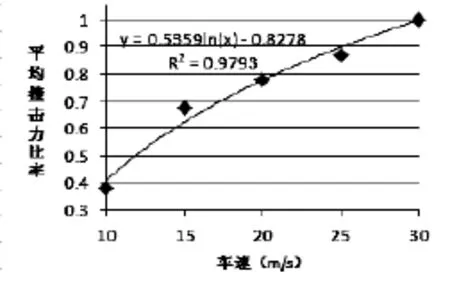
图12 撞击力平均值拟合关系图
经过对不同速度下撞击力的处理, 可以看出撞击力大小与速度呈非线性关系, 撞击力与速度的关系符合对数函数的关系, 拟合后得到的公式为
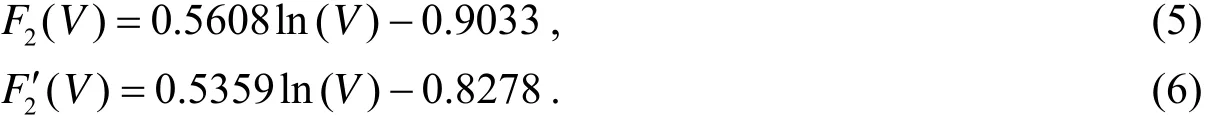
2.4 撞击荷载计算公式
上述基于Ansys/Ls-dyna建立的车桥碰撞模型进行了仿真分析, 并根据仿真分析结果拟合出了撞击力大小分别与车重及车速的关系式, 分别将(3)、(4)、(5)、(6)代入撞击力曲线拟合公式(1)、(2)即可得到

两式中只有R和R′未知, 利用相关多参数曲线拟合和已经确定的函数形式, 将所有工况结果进行拟合, 得到R=3.0321,R′=1.5515, 代入公式(7)、(8)即可得到撞击力关于车重和车速的计算公式为

其中, 质量M的单位为t, 速度的单位为m/s, 撞击力的单位为106N. 从公式中可以看出撞击力最大值大致为平均撞击力的2倍, 这与规范规定的撞击力最大值与平均撞击力之间的关系相吻合, 说明通过仿真模型得到的拟合公式适用于超高车辆撞击桥梁上部结构撞击力的计算.
3 应用比较
国内外关于受撞桥梁结构撞击力的规定有很多, 我国桥梁设计通用规范规定车辆行驶方向撞击力大小为1000kN, 美国规范规定车辆行驶方向撞击力大小为1800kN, 欧洲规范规定的较为详细(高速公路, 国道及主干道为1000kN, 乡村地区道路为750kN, 城市道路为50kN). 而根据本文对影响撞击力因素的研究, 撞击力大小受车重及车速的影响较大, 所以撞击力不能仅仅只规定为一定值. 此处选用一辆8t车以17m/s的速度撞击桥梁上部结构为例, 将本文所得到的撞击力计算公式与其它文献规定进行比较. 结果见表2.
由表2可知, 文[3]中撞击力结果与本文结果相当, 从而可知本文拟合的撞击力计算公式适用于超高车辆撞击桥梁上部结构撞击力的计算.

表2 撞击力比较
4 结论
本文对超高车辆撞击桥梁上部结构进行仿真分析, 研究了桥梁在不同车重及车速撞击作用下的撞击力大小. 通过对撞击力大小的比较, 得出受撞桥梁撞击力随车重及车速的增大而增大, 且存在一定的关系,从而可知规范规定的撞击力大小为一定值存在缺陷, 再经过多参数曲线拟合分析, 拟合出撞击力计算公式. 将本文结果与相关文献进行比较, 验证了撞击力拟合公式的可靠性, 从而为相关工程设计及加固提供参考.
[1] 王军华, 叶晓彦. 立交桥试用激光防撞预警系统[N]. 北京晚报, 2007-07-31(12)
[2] JTG D61-2004, 公路桥涵设计通用规范[S]. 北京: 人民交通出版社, 2004
[3] 陆新征, 何水涛, 黄胜楠. 超高车辆撞击桥梁上部结构[M]. 中国建筑工业出版社, 2011
[4] Woison G.Design against collision[J]. Schiff&Hafen,1979,31(2): 1059~1069
[5] A.C.W.M Vrouwenvelder.Design for Ship Impact According to Eurocode 1,Part 2.7,Ship Collision Analysis[S]. A.A.Balkema, Rotterdam,1998.
[6] AASHTO 1991.Guide Specifications and Commentary for Vessel Collision Design of Highway Bridges[S]. American Association of State Highway and Transportation Official,Washington D.C.
[7] TB 10002.1-2005. 铁路桥涵设计基本规范[S]. 北京: 中国铁道出版社, 2005
[8] 陆新征, 张炎圣, 宁 静, 等. 超高车辆与立交桥碰撞的高精度非线性有限元仿真[J]. 石家庄铁道学院学报, 2007, 20(1): 29~34
[9] 白金泽. LS-DYNA3D理论基础与实例分析[M]. 北京: 科学出版社, 2005
[10] 陶 鹏. 船桥碰撞力仿真分析与模型试验研究[D]. 南京: 南京航空航天大学硕士学位论文, 2012
[11] 马祥禄. 跨线桥在超高车辆撞击下的动态响应分析[D]. 北京: 北京工业大学硕士学位论文, 2009
[12] 张炎圣, 陆新征, 叶列平, 等. 超高车辆桥梁上部结构碰撞荷载精细有限元模拟与简化计算[J]. 工程力学, 2011,28(1): 116~123
[13] 何水涛, 陆新征, 卢 啸, 等. 超高车辆撞击钢桥上部结构模型试验研究[J]. 振动与冲击, 2012, 31(5): 31~35
[14] 刘建成, 顾永宁, 胡志强. 桥墩在船桥碰撞中的响应及损伤分析[J]. 公路, 2002, 10: 33~41
[15] 魏 朗. 车辆碰撞事故解析计算中主要影响因素误差界定[J]. 中国公路学报, 2000,13 (1): 109~113
[16] 林建飞, 郑振飞, 卓卫东. 泉州后渚大桥船撞力试验研究[J]. 中国公路学报, 2003, 116(12): 57~60

该程序严格按设计步骤编写, 程序语句附有注释, 运行结果在命令窗或图形窗中都有显示. 从绘出的幅频曲线可以测出ω=0.3π时衰减2.22dB,ω=0.6π时衰减8.376dB, 通带指标并不符合技术要求. 如果改用Ωc=Ωcs重新设计, 测出ω=0.3π时衰减1.671dB,ω=0.6π时衰减5.713dB, 阻带指标不符合技术要求. 这是因为实例的阻带衰减不大, 阻带边界频率离采样频率也不远, 导致频谱混叠严重的结果, 可通过适当调整3dB截止频率的位置或增加滤波器阶次解决.
4 结束语
利用脉冲响应不变法设计的IIR数字滤波器, 其时域特性逼近好, 频率变换线性, 但存在频谱混叠,故只适合设计锐截止低通类滤波器. 采样周期虽不参与设计, 但在设计过程中参与了计算. 为了避免计算机有效字长效应引起的误差, 取值不宜过大或过小. 3dB截止频率不同对边界指标有一定的影响, 需根据实际灵活选取. 脉冲响应不变法既是设计IIR数字滤波器的基本方法, 也是双线性变换法的基础. 文中列举的巴特沃斯低通滤波器设计实例, 对其它各型滤波器设计也有一定的参考价值.
参考文献
[1] 高西全, 丁玉美. 数字信号处理[M]. 第3版. 西安: 西安电子科技大学出版社, 2008: 178~184
[2] 吴镇扬. 数字信号处理的原理与实现[M]. 南京: 东南大学出版社, 2001: 75
[3] 刘顺兰, 吴 杰. 数字信号处理[M]. 西安: 西安电子科技大学出版社, 2003: 165, 156~162
[4] 张志勇. 精通MATLAB6.5[M]. 北京: 北京航空航天大学出版社, 2003
[5] 陈怀琛, 吴大正, 高西全. MATLAB及在电子信息课程中的应用[M]. 第2版. 北京: 电子工业出版社, 2004
[6] 吴湘淇. 信号、系统与信号处理的软硬件实现[M]. 北京: 电子工业出版社, 2002
The Simulation Analysis of the Collision Load for Impacted Bridge
LIU Xiao-yan, ZHU Zhou-zhou, JIANG Tai-xin, CHEN Cai-peng
(Institute of Civil and Architecture, Changsha University of Science & Technology, Changsha 410015, China)
The bridge superstructure will have been lots of loss when impacted by the over-high truck. In order to grasp the situation of loss for the bridge structure, we need to determine the collision load. This paper bases on the simulation model to research the collision load which caused by the car-bridge collision. The simulation model built by the Ansys/Ls-dyna to analysis the value and variation for the collision load when the over-high truck impact the bridge structure in different quality and velocity. This work get through the multi-parameter curve fitting to obtain the collision load formula for the impact bridge, compare results of this paper with the relevant literatures about the value of collision load to test the formula adapting to calculate the collision load, thus, giving the reference to the relevant design and consolidate.
over-high truck; impact; bridge structure; simulation model; collision load
U441
: A
: 1672-5298(2015)04-0063-06
2015-09-02
刘小燕(1963− ), 女, 湖南桃江人, 硕士, 长沙理工大学土木与建筑学院教授. 主要研究方向: 桥梁结构分析与工程控制
