接触面对驳船撞击桥墩动力响应的影响

2018-09-20邹毅松王银辉

重庆交通大学学报(自然科学版) 2018年9期

邹毅松，刘磊，王银辉，罗征

(1. 重庆交通大学土木工程学院，重庆 400074； 2. 浙江大学宁波理工学院土木建筑学院，浙江宁波 315100)

0 引言

船舶航行对航道桥梁产生了严重的威胁[1]，船舶碰撞下桥梁安全问题一直是桥梁工程的重要研究领域。目前学者针对带球鼻艏船舶对桥梁结构碰撞开展研究，取得的成果主要集中在基于概率统计模型的船撞风险和防撞能力评估[2-4]、基于弹塑性有限元方法的船撞问题研究[5-6]、关于简化动力模型的研究[7-8]等方面。

船艏形式和刚度对船桥碰撞的动力响应有较大的影响。作为内河航道主要船型的驳船，其船艏一般呈扁平状，刚度较大，与球鼻船艏有很大差异。为此，张景峰等[9]对比了带球鼻艏散装货船与内河驳船撞击桥梁动力响应的差异；G. R. CONSOLAZIO等[10]、 Y. SHA等[11]、 C. M. D. WILSON等[12]研究了驳船撞击下桥墩及其他下部结构撞击力-撞深的关系及非线性问题；P. YUAN等[13]、段敏[14]通过数值模拟及试验研究了方形与圆形两种截面桥墩对驳船撞击力的影响，发现不同船艏形式和不同桥墩截面形式所导致的船撞动力响应差异实质是船-桥接触面和接触刚度。驳船的扁平船艏与不同形状桥墩的接触区域存在明显差异，驳船船艏与桥墩之间的碰撞接触面成为影响碰撞动力响应的重要因素，如图1。

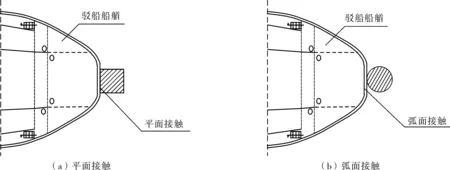
图1 驳船船艏与不同桥墩的接触形式Fig. 1 Contact forms between barge bow and different piers

笔者利用有限元分析方法，研究驳船与桥墩撞击时，不同接触面(平面接触和弧面接触)对撞击力时程曲线和撞击力-撞深曲线的影响，并根据驳船撞击作用下桥墩的最大动力响应等效原则，探讨可供桥墩设计计算所用的等效撞击力。研究结果可为桥梁设计时的等效撞击力取值及为防撞设施外形设计提供参考。

1 计算模型

1.1 驳船模型

采用500DWT驳船，满载排水量650 t，主甲板高3.22 m，总长53.3 m，型深2.9 m，型宽12.5 m，吃水深度2.3 m，如图2。

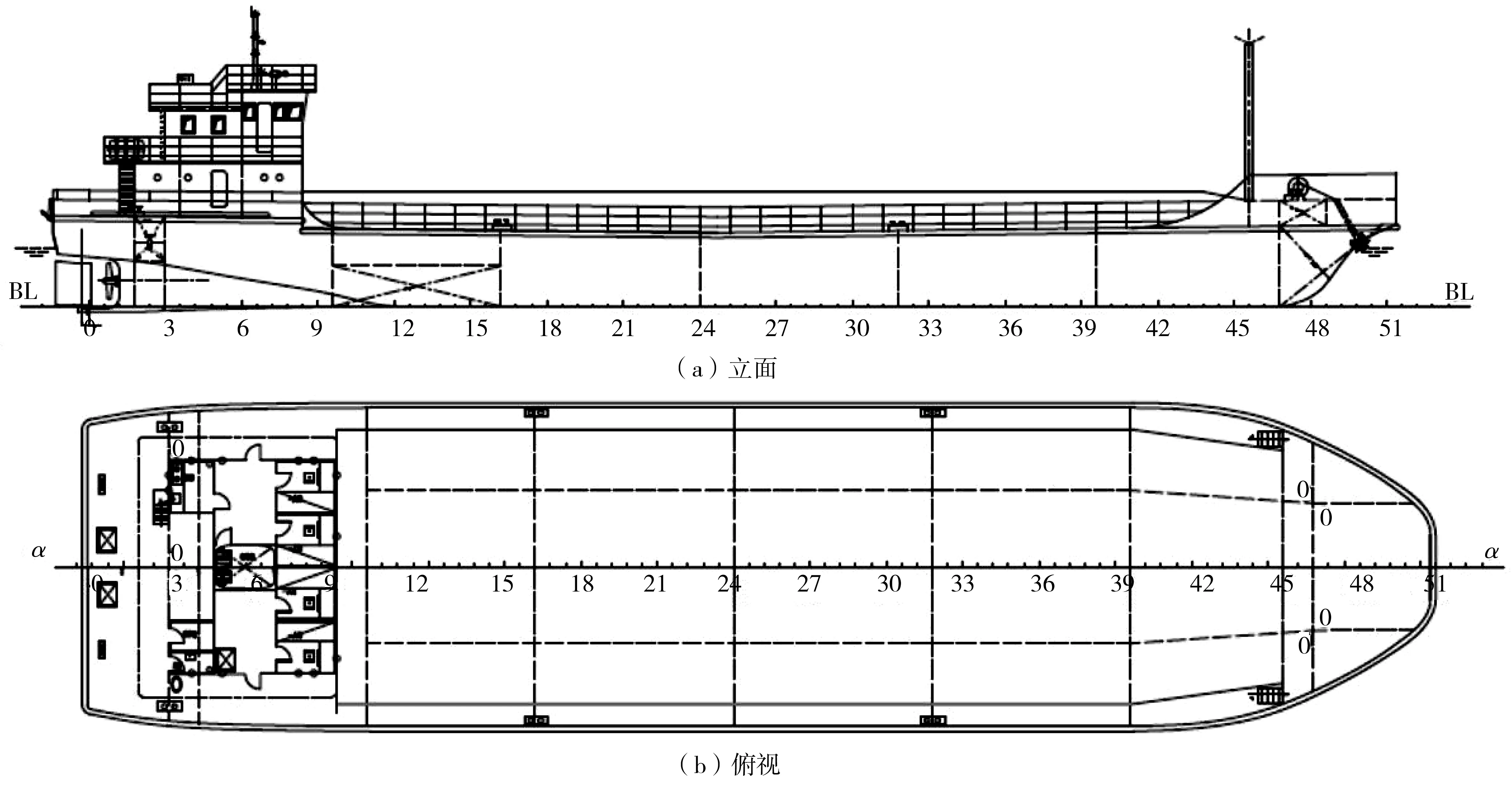
图2 500DWT驳船(单位：m)Fig. 2 The 500DWT barge

在ANSYS/LS-DYNA中建立500DWT驳船有限元模型。大量研究表明，在整个碰撞过程中，船艏会发生很大的塑性变形，是吸收耗散碰撞动能的主要部分，而除船艏以外的其它部分很少在消耗能量中起作用。故在考虑兼顾计算精度与计算效率的情况下，将驳船分为船艏、船身、船尾3段建模，其中船艏部分精细到每根船体骨架，另外2部分相对较简化，船体质量通过质量块施加，如图3。

图3 500DWT驳船有限元模型Fig. 3 Finite element model of 500DWT barge

船身、船尾及船艏外壳采用SHELL163板壳单元，船艏骨架采用BEAM161梁单元，船体质量块采用SOLID164实体单元。由于在碰撞过程中，船艏钢材处于非线性状态，所以船艏钢材采用Cowper-Symonds本构模型[15]，船艏以外船体部分结构采用各项同性(Isotropic)弹性模型，相应参数见表1。

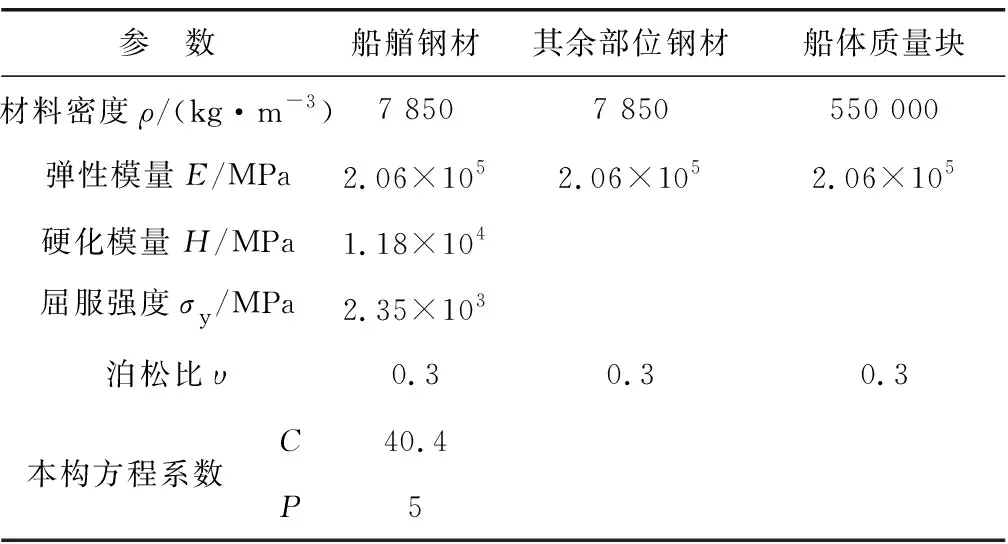
表1 驳船钢材参数Table 1 Barge steel parameters

船体下部设置150组采用COMBIN165单元的非线性弹簧模拟水体浮力，弹簧参数采用1号力/位移关系曲线。

1.2 桥墩模型及接触条件

桥墩采用SOLID164实体单元，船桥碰撞时，以船艏构件变形、破坏吸收能量为主，桥墩吸收能量较少[16]，船桥碰撞研究和数值分析时，常将桥墩假定为刚性。

首先，当船艏与桥墩接触的瞬间，由于船艏内部的桁架不能确定先发生变形的部位，故将驳船船艏内部各根桁架单元之间的接触定义为单面自动接触(ASSC)。然后，通过点面固连接触(TNTS)及面面固连接触(TSES)将船艏外壳与内部桁架相互固接，使船艏外壳与内部桁架在高速碰撞过程中始终为一个整体，避免出现桁架脱落现象。最后，采用面面自动接触(ASTS)定义桥墩与船艏外表面的接触，考虑到船艏与桥墩界面间的相对摩擦，设置静摩擦系数fj=0.15，动摩擦系数fd=0.10。

2 驳船-桥墩撞击特征分析

为了考察船艏与桥墩接触形式和尺寸对撞击力、撞深的影响，避免桥墩刚度等因素的干扰，将桥墩假定为底部固接的刚性柱。

参照文献[13]提出的接触尺寸与驳船船艏宽度的比值α，当驳船船艏与桥墩表面接触为平面时，该比值定义为α1；当驳船船艏与桥墩表面接触为弧面时，该比值定义为α2：

(1)

(2)

式中：bc为桥墩平接触面宽度；B为驳船船艏的宽度；D为桥墩弧形接触面圆弧直径。

α1表达了驳船与桥墩接触的尺寸，而弧面接触其实接触区域很小，α2仅表达了驳船与桥墩接触区发展趋势，能反映船艏变形后接触区域的增大程度。

2.1 接触面宽度的影响

2.1.1 驳船与桥墩平面接触

为了了解在驳船与桥墩平面接触时，接触面尺寸对撞击力时程的影响，分别建立α1=0.25、0.50、0.75、1.00等4种尺寸的平接触面桥墩，设驳船初始速度v=3 m/s，进行驳船碰撞刚性桥墩的有限元分析，平面接触下驳船与桥墩模型整体情况如图4。

不同α1值时碰撞的撞击力-时程曲线和撞击力-撞深曲线如图5。由图5可见：

1)碰撞呈现明显的瞬时弹性碰撞阶段和非弹性碰撞阶段[图5(a)]。

2)瞬时弹性碰撞阶段，α1值越大，撞击力越大，非弹性碰撞阶段撞击力几乎为定值；非弹性碰撞阶段，α1值越大，撞击力变化越小，持时越短，而α1较小时，非弹性碰撞阶段撞击力呈一定上升趋势。

3)α1值越大，撞深越小，最大撞深出现在非弹性碰撞阶段，与撞击力峰值出现的时刻不同。

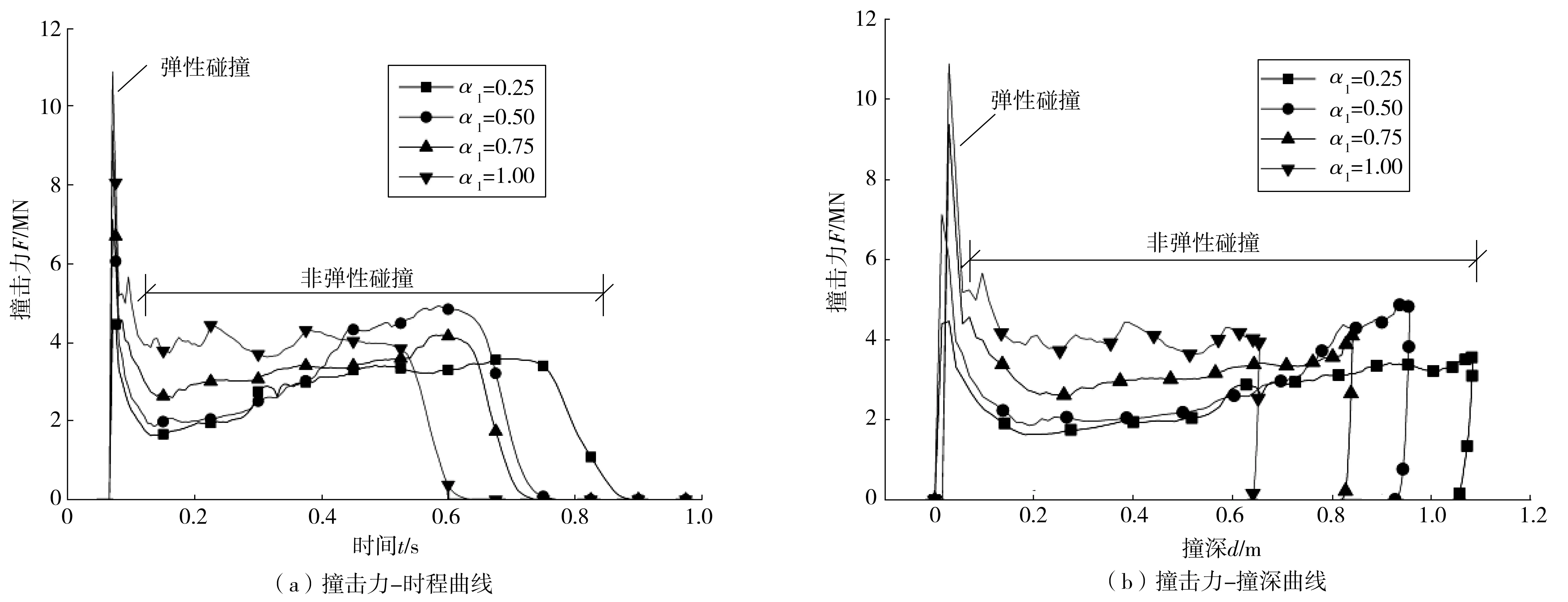
图5 平面接触时撞击力-时程曲线、撞击力-撞深曲线Fig. 5 Impact force-time history curve and impact force-crush depth curve with plane contact

2.1.2 驳船与桥墩弧面接触

为了保证接触面形状不发生变化，假定弧面能够延伸足够长，故采用α2=0.25、0.50、0.75、1.00等4种尺寸的圆弧形接触面桥墩。

图6为α2=0.75时的整体模型。图7为该桥墩遭受驳船以3 m/s速度碰撞的撞击力-时程曲线及撞击力-撞深曲线。

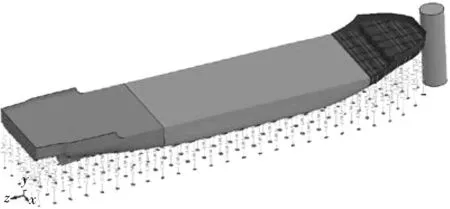
图6 弧面接触时驳船撞击桥墩有限元分析模型Fig. 6 FEA model of barge impacting pier with arc contact

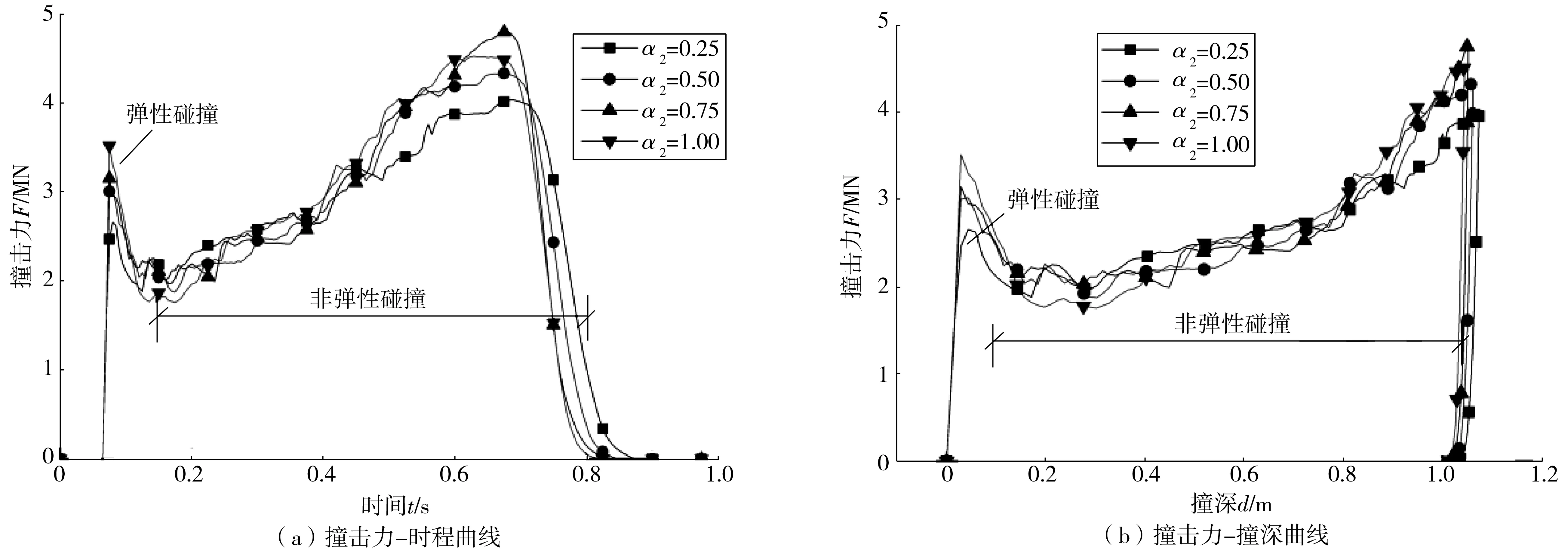
图7 弧面接触时撞击力-时程曲线、撞击力-撞深曲线Fig. 7 Impact force-time history curve and impact force-crush depth curve with arc contact

由图7可见，弧面接触时撞击力及撞深有如下特点：

1)撞击力有明显的瞬时弹性阶段和非弹性碰撞阶段，但α2的变化不会引起撞击力、撞深的显著改变。

2)撞击力在非弹性碰撞阶段的峰值比瞬时弹性碰撞阶段大，之后撞击力迅速减小到0。

3)撞击力峰值与最大撞深同时出现在非弹性碰撞过程的末尾。

2.2 接触面形状的影响

分析可见，由于驳船有较宽平的船艏，所以驳船与桥墩发生碰撞时，具有明显的瞬时弹性碰撞区域，瞬时撞击力较大。随着船艏发生变形、破坏，撞击力-时程曲线进入了一个缓和平台段。当平面接触时，由于接触面不变，撞击力随时间变化很小；而当弧面接触时，随撞深的增大，接触面逐渐增大，撞击力也逐渐增大。相同工况下，弧面接触时，撞深到达最大；平面接触时，随着接触面积减小，撞深相应增大。可见弧面接触可认为是接触面极小的平面接触。

驳船分别撞击平接触面及弧面接触面的桥墩，船艏的损伤情况存在明显差异。图8为最大撞深时的变形形状和Mises应力云图。可见平面接触下船艏变形面平坦，桥墩嵌入深度较浅，但损伤区域较宽，Mises应力主要分布在船艏端部及撞击区两侧；而弧面接触下，船艏变形呈圆弧状，受损区域较窄，最大嵌入深度较大，Mises应力分布深入船艏。

图8 船艏变形及应力云图Fig. 8 Bow deformation and stress nephogram

张景峰等[9]分析了带球鼻艏货轮与驳船撞击桥墩的响应差异，其实质也是碰撞接触面的因素。由于球鼻艏尺寸小，更易破坏吸能，导致碰撞时无明显瞬时弹性碰撞区域，撞深较大。

2.3 驳船撞击速度的影响

撞击速度是影响撞击力的重要因素，图9给出了α1=α2=0.75时不同撞击速度下，2种接触形式的撞击力时程曲线。

由图9可见，对于平面接触，碰撞速度较低时，非弹性碰撞阶段撞击力发展平稳且与瞬时弹性碰撞的撞击力峰值相差甚远；而当撞击速度较高时(4～5 m/s)，非弹性碰撞阶段后期撞击力出现明显的二次增长现象，与撞击力峰值的差距也逐渐减小。对比图9(a)、(b)可见，随着撞击速度的增长，2种接触的时程曲线形状基本趋于相同。

2.4 力学机理分析

由于驳船船艏为扁平状，接触面积越大，则碰撞瞬时参与抵抗撞击的船艏钢构件数量就越多，船艏抗撞击变形的钢构件数量越多；接触刚度越大，反映在瞬时弹性碰撞阶段的撞击力峰值也越大。弧面接触时接触面积极小，故参与抵抗撞击的钢构件数量很少，瞬时弹性碰撞撞击力相对较小。

瞬时撞击发生后，船艏钢构件即开始产生变形，碰撞进入非弹性碰撞阶段。平面接触或接触面较大时，参与抵抗的钢构件数量几乎不变，此时撞击力也几乎不变，因钢构件逐渐进入塑性变形阶段，故撞深持续增大。当接触面较小或弧形接触时，随着撞深的增大，桥墩逐渐嵌入船艏，参与抵抗撞击的构件数量会逐渐增多(图10)，此时就会产生非弹性碰撞阶段撞击力二次增大现象(图9)。

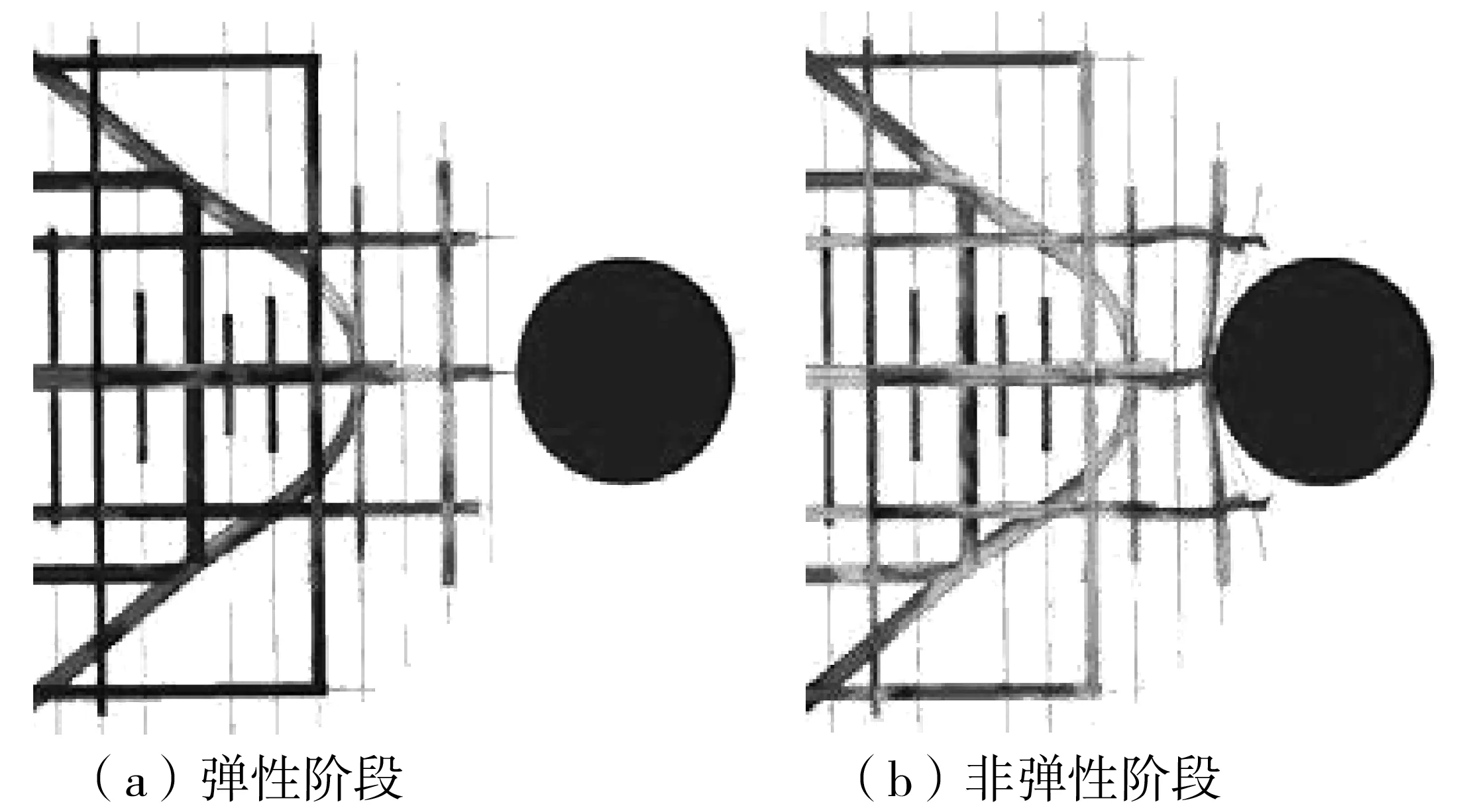
图10 船艏钢材变形情况Fig. 10 Deformation condition of bow steel

而当船速较大时，即使接触面较大的情况，也可能因撞深过大而造成后期抵抗碰撞的船艏钢构件数量增多，造成非弹性碰撞阶段撞击力二次增大现象。

从能量的角度分析，平面接触更宽阔平坦的损伤区域比弧面接触狭窄深陷且呈圆弧状的损伤区域有更多的船艏骨架钢材同时参与变形耗能(图11)，从而使碰撞动能更快地转化为船艏变形能，这也是2种接触撞击力和损伤情况存在差异的重要机理。

图11 能量-时程曲线Fig. 11 Energy-time history curves

所以，驳船碰撞桥墩时，无论瞬时弹性碰撞还是非弹性碰撞，撞击力大小实际上取决于船艏损伤区域的钢构件参与抵抗的数量和产生变形破坏程度，实际上是船艏抵抗碰撞的刚度和耗能速率，但此刚度与接触形状及接触尺寸密切相关。

3 驳船撞击下桥墩动力响应

分析可知，撞击力-时程曲线与接触面积密切相关，有瞬时弹性碰撞最大撞击力和非弹性碰撞最大撞击力。但对桥墩而言，哪个阶段的撞击力产生的结构响应更大，设计时应如何取用撞击力设计荷载还亟待讨论。为此，笔者将船速v=3 m/s，α1=0.75工况下的碰撞时程力作为激励输入到实际桥墩模型中，分析桥墩结构的动力响应。

桥墩模型为一高18 m钢筋混凝土桥墩，如图12，墩身为3 m × 3 m的矩形截面，撞击点位于基础之上9 m处，墩顶设置10 000 t集中质量模拟上部结构。

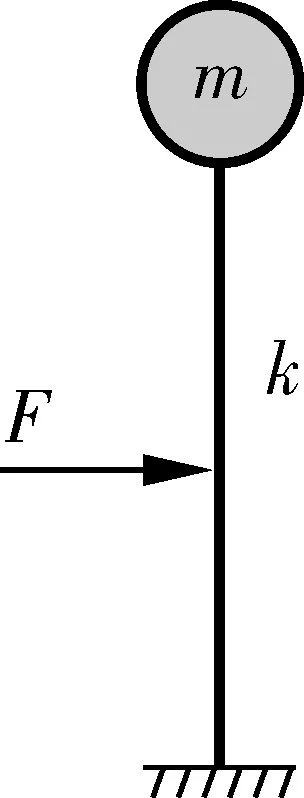
图12 桥墩模型示意Fig. 12 Sketch map of pier model

为了简化分析，不考虑基础的桩土相互作用，墩底固结。结构采用Rayleigh阻尼[17]，即：

[C]=α[M]+β[K]

(3)

式中：α为质量阻尼系数；β刚度阻尼系数。α、β通过振型阻尼比计算得到，即：

(4)

(5)

式中：ωi、ωj分别为结构的第i、j固有频率，取值i=1，j=2；ξi、ξj为相应于第i、j振型的阻尼比，取值ξi=0.03，ξj=0.07。

3.1 桥墩结构动力响应

在撞击时程力的作用下，墩顶位移和墩底弯矩随时间不断变化，如图13。

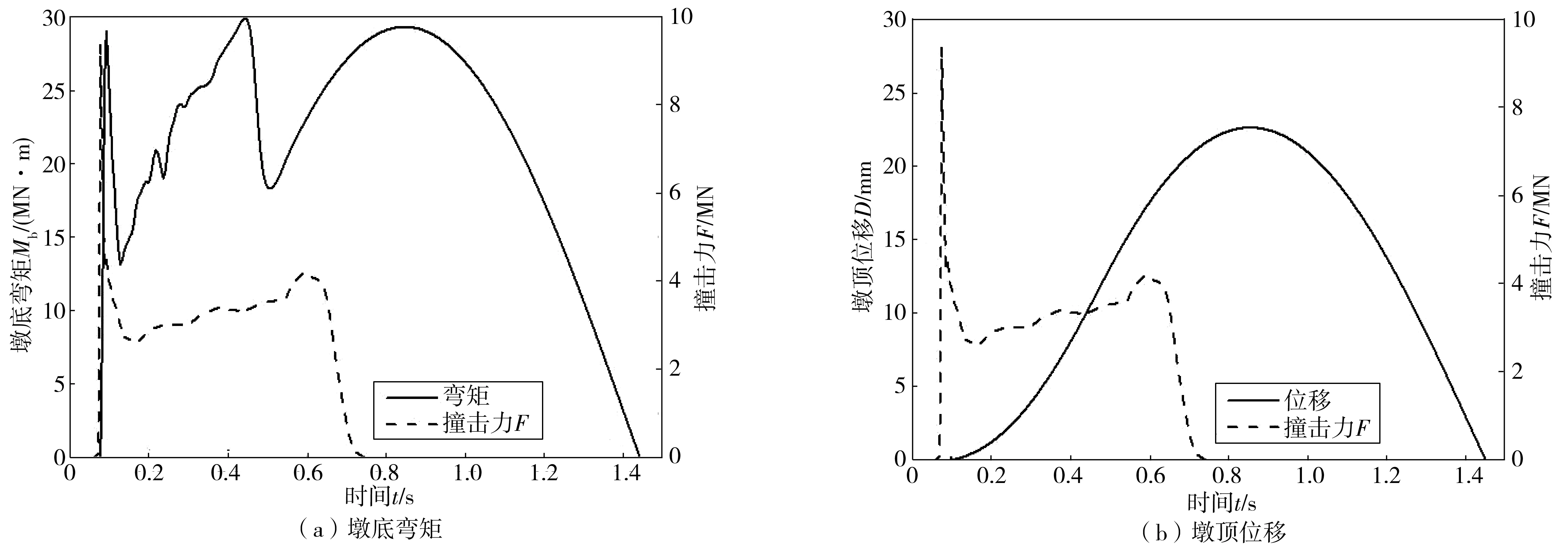
图13 驳船撞击下桥墩力响应Fig. 13 Structure response of pier under barge impact

碰撞发生后，墩底弯矩出现3次峰值，分别在瞬时弹性碰撞时、非弹性碰撞荷载持续增长段、碰撞力消除后达到峰值；而墩顶位移持续增大到峰值再减小至0，位移峰值与碰撞力消除后的墩底弯矩峰值同步出现，且同时减小至0。由此可见，在非弹性碰撞区段，碰撞力与墩底弯矩和墩顶位移的变化规律不同步，与动力响应过程中桥墩质量、刚度、阻尼等均密切相关。可见瞬时弹性碰撞阶段撞击力峰值和非弹性碰撞阶段撞击力峰值均不能完全真实的反映桥墩结构的动力响应，不能简单地利用撞击力峰值作为等效静力计算桥墩内力和位移。

3.2 等效撞击力

无论接触面形状、大小如何变化，驳船与桥墩的撞击力均呈现出明显的瞬时弹性碰撞阶段和持续性的非弹性碰撞阶段，而不同接触形状下两阶段的峰值相对大小不同(平面接触中瞬时弹性撞击力峰值较大，弧面接触中非弹性撞击力峰值较大)。由于瞬时弹性阶段撞击力峰值不能直接作为计算桥墩所承受的碰撞荷载，在桥梁设计工作中，若以瞬时弹性碰撞阶段峰值作为等效静力来替代船舶对桥梁的撞击力，往往会因撞击力峰值较大，使得设计过于保守，而采用非弹性阶段碰撞的峰值作为等效静力也缺乏依据。

为了探明哪一阶段的撞击力才是影响桥墩结构动力响应结果的主导因素，保证桥墩整体结构的安全性，进而得知何种接触形式对保护桥墩最有利，且为了正确反映桥墩结构响应，提出了等效撞击力的概念。在碰撞位置作用等效静力，使其产生的静力效应(墩底弯矩或墩顶位移)达到与撞击力相同效果的动力响应峰值(最大墩底弯矩或最大墩顶位移)。

等效撞击力分为基于弯矩的等效撞击力和基于墩顶位移的等效撞击力两种。桥墩安全性设计要求采用基于弯矩的等效撞击力，而涉及上部结构安全时则采用基于墩顶位移的等效撞击力，如图14，图中：F(t)为撞击时程力；Dmax为墩顶最大动位移；Feq为等效撞击力；H为桥墩高度；Deq为等效撞击力下墩顶静位移，Deq=Dmax。

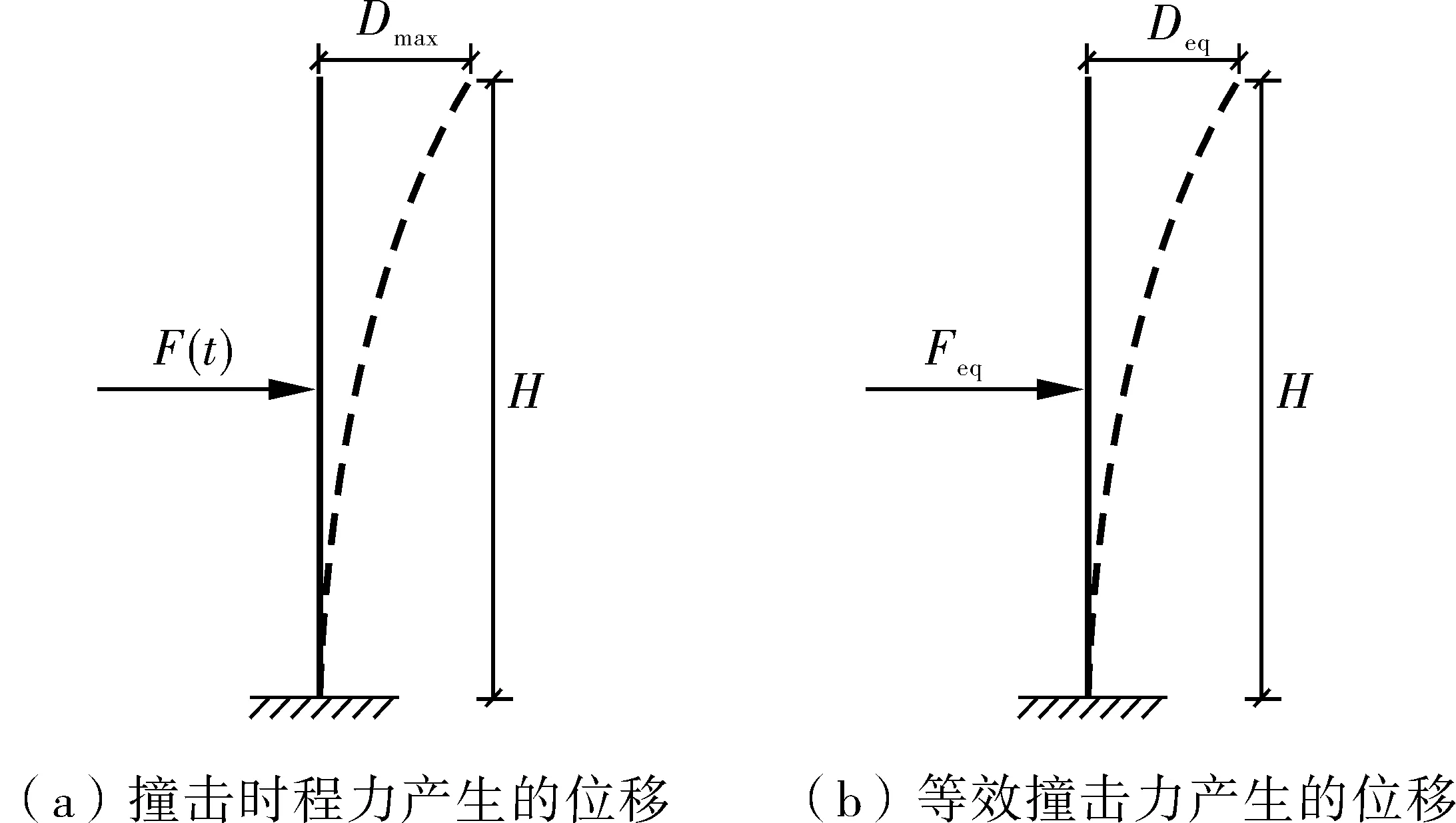
图14 等效撞击力及等效位移Fig. 14 Equivalent impact force and equivalent displacement

为了表征等效撞击力与碰撞动力荷载的关系，定义撞击力的等效折减系数δ：

δ=Feq/Fmax

(6)

式中：Feq为达到与动力响应相同墩顶位移的等效撞击力；Fmax为撞击力-时程曲线中的撞击力峰值。

平面接触与弧面接触2种情况所采用的桥墩截面惯性矩不同，不应直接进行对比。故将2种接触形状下各自不同尺寸所得的撞击力时程分别加载于同一桥墩(平面接触工况使用一个桥墩模型，弧面接触使用另一个桥墩模型)，再分别对比所得的等效折减系数。

表2为驳船速度v=2 m/s的工况时，不同接触条件下等效折减系数δ。

可见弹性碰撞阶段撞击力峰值不能直接反映桥墩结构的动力响应情况。等效折减系数δ随α1(或α2)增加而减少，表明接触面积越大，峰值撞击力更加偏离桥墩的真实动力响应情况。若将其作为桥墩防撞设计值，则会导致结果偏大，设计偏保守的情况。故需要采用等效撞击力来更真实地反映驳船对桥墩结构整体的动力响应。而整体对比，平面接触的等效折减系数小于弧面接触，说明平面接触情况下的峰值撞击力距真实情况有更大的偏差，所以等效撞击力对于平面接触的情况有更大的实用价值。

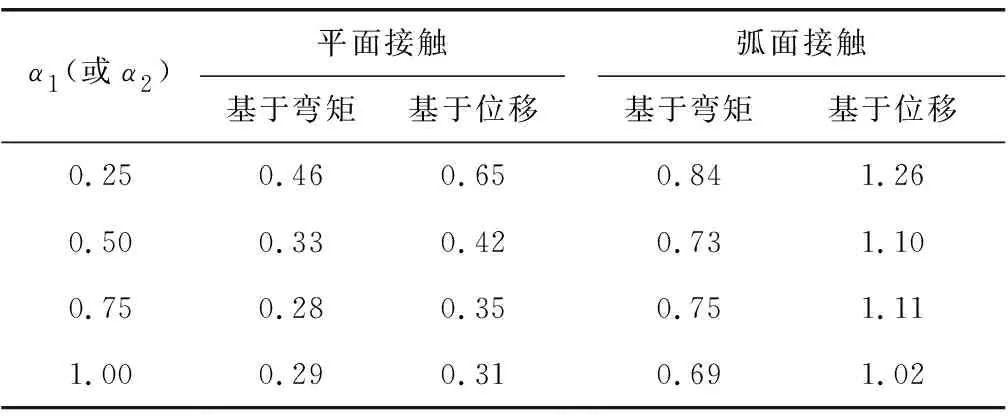
表2 等效折减系数δ

由于各工况条件存在多个变量，包括船速、接触面形状、接触面尺寸等，这些变量都会导致撞击时程力发生变化，而各规范中大多未将除船速外的条件予以考虑。为比较等效撞击力及各规范撞击力，探明其中何种结果能够更为准确的体现桥墩结构的动力响应，笔者采用单一的工况进行讨论，未对多条件进行比较。

图15为将本例中v=3 m/s，α1= 0.75工况下求得的等效撞击力与碰撞2个阶段的撞击力峰值以及国内外各规范计算的撞击力值(等效静力)对比。由于我国JTG D 60—2014《公路桥涵设计通用规范》、TB10002.1—2005《铁路桥涵设计基本规范》及欧洲统一规范[18]中没有专门的驳船撞击力设计值，笔者采用内河船舶撞击力设计值。

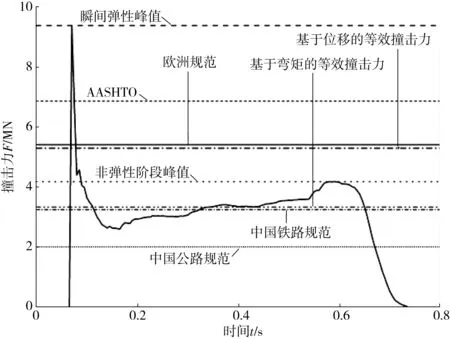
图15 等效撞击力Feq与各规范取值比较Fig. 15 Comparison of Feq and the values of various specifications

由图15可见，基于弯矩的等效撞击力和基于墩顶位移的等效撞击力存在较大差异，前者小于非弹性碰撞阶段的撞击力峰值，而后者则大于非弹性碰撞阶段的撞击力峰值。中国公路规范JTG D 60—2014的撞击力取值偏小且与数值模拟分析结果相差较大；中国铁路规范TB 10002.1—2005撞击力取值与基于弯矩的等效撞击力接近；欧洲统一规范内河船舶撞击力设计值和美国AASSTO规范[19]驳船撞击力设计值介于瞬时弹性峰值和非弹性阶段峰值之间，其中欧洲统一规范计算结果与基于墩顶位移的等效撞击力非常接近。

总体而言，AASSTO规范、欧洲统一规范以及中国规范计算的等效撞击力均为单一值，或接近于基于弯矩的等效撞击力，或接近于基于墩顶位移的等效撞击力。根据碰撞荷载作用下桥墩的动弯矩和动位移时程曲线，单一的等效撞击力不能满足桥墩和上部结构的安全设计需要。在实际工程应用中，可根据结构的需要选取相应的等效撞击力，但相应的等效撞击力计算公式需要进一步研究，当然也可以通过有限元方法计算得到。