电动飞翼布局无人机设计研究

王刚，胡峪，宋笔锋

(西北工业大学航空学院，陕西西安710072)

0 引言

小型电动无人机以电池为能源，航时从0.5 h到2.5 h不等，在侦查、监控和跟踪等军民领域中得到了广泛应用。采用常规布局的手掷无人机，由于尾翼的存在造成了飞机阻力增大，重量增加，留空时间缩短;而采用无尾布局的无人机，目前多使用反弯度翼型，造成最大可用升力系数减小，翼载荷下降，展弦比减小，导致飞机重量和抛射速度增大。为改善飞行性能，本文对使用正弯度翼型的飞翼式布局无人机开展了总体设计计算研究，基于遗传算法优化配置机翼几何和舵面设计参数，通过参数分析，探讨了电池容量和航时对无人机性能的影响，提出了采用正弯度翼型飞翼布局无人机的优化设计方法。

1 设计思想

本文在设计飞翼布局电动无人机过程中选用特定的正弯度翼型，具备较小俯仰力矩的同时，具有较高的失速迎角和最大可用升力系数。最大可用升力系数的提升会增加机翼载荷，从而减小机翼面积，增大展弦比，进而减小无人机尺寸和重量。展弦比的提高，有助于在翼根采用襟翼，可进一步降低手掷起飞速度。与此同时，展弦比的增大使得无人机升阻比提高，一方面在电池容量固定情况下，航时得以提升;另一方面在给定作战时间情况下，带来无人机重量和尺寸的改善。

对于使用正弯度翼型带来的纵向配平问题，经过总体设计、CMARC气动力纵向稳定性分析以及遗传算法参数优化发现，只要机翼后掠角、扭转角、升降副翼和襟翼设计配置合理，升降副翼偏转较小角度即可保证无人机在巡航和盘旋阶段达到纵向稳定，同时升阻比损失不大，最终改善其性能。

基于此，本文利用飞机任务段总体设计方法［1］，采用正弯度翼型，以一架航时4 h，有效装载500 g的飞翼布局手掷电动无人机为算例，开展计算研究。

2 算例

2.1 设计指标

算例设计目标分为两种:算例1是固定12 Ah电池容量，以航时为最优目标设计;算例2是指定任务时间，巡航和盘旋各为2 h，以尺寸和重量为最优目标设计。

起飞质量不得超过3 kg，手掷抛射角为30°，手掷起飞速度为8 m/s［2］。采用腹部着陆方式，下滑角为10°，着地速度为9 m/s。飞行高度为100～300 m，任务载荷为0.5，巡航速度为18 m/s，以 μ=45°，Vlo=18 m/s进行作战机动盘旋。

2.2 重量模型

2.2.1 电池重量模型

聚合物锂离子电池在实际工作中，其有效容量依赖于它的放电电流，若放电电流非额定值，有效容量会有所不同，放电时间也随之改变，该值可通过Peukert定理来计算。电池放电过程中，电压会降低，但其压降值缓慢而温和直至完全放电，故可视之为线性变化［3］。对于给定电池容量C和所需功率P，通过如下数值积分步骤来求解电池在变化电压条件下的放电时间［3］:

(1)在初始电压V0下，所需的初始电流为:(2)对于初始电流i0，有效初始电池容量为:

式中，H为电池额定放电时间;n为Peukert常数。

(3)选取时间间隔 Δt和下标 j=0，1，2，…，N。

(4)由于电压线性变化，Δt后电压值为:

式中，k为压降系数;Vend为终止放电电压。

(5)电压降低，为获得稳定功率引起的电流变化为:

(6)剩余电池容量Cj+1(t):

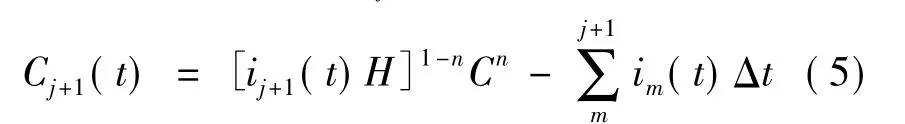
步骤(4)～(6)不断迭代，直到Cj+1(t)≈0迭代结束。电池的实际放电时间即为t=jΔt。

目前多数聚合物锂电池的能量密度为150 Wh/kg，放电倍率为3C，Peukert常数为1.1，这里采用三节电池串联。不同所需功率下，运用以上数值积分方法进行计算，结果如图1所示。

图1 不同电池容量放电时间与功率的关系

对上图进行线性插值，结合总体设计功率重量比得到放电时间t关于电池容量C和所需功率P的函数关系，再根据电池的比容量，可推导出电池组关于无人机的重量系数f1。

2.2.2 电机重量模型

对已有微型外转子无刷电机重量和功率关系进行统计，通过线性拟合，电机重量Wm与其功率Pm关系可表示为:

设计过程中，需考虑电机调速器效率ηd、电机效率ηm和螺旋桨效率ηp，一般取其值均为80%［2］。

由无人机功率重量比，结合电机重量与功率关系可得电机关于无人机的重量系数f2。

2.2.3 起飞重量

全机结构材料采用航空层板，蒙皮使用密度为1 500 kg/m3的玻璃钢。全机结构重量为Ws，通过机翼、小翼和机身的面积估算可得。任务载荷重量Wl=0.5 kg。根据电池和电机重量系数，无人机起飞重量为［4］:

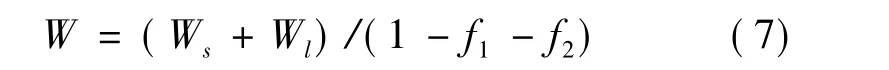
2.3 机翼设计

机翼采用正弯度翼型，使用XFOIL翼型分析软件，从纵向俯仰力矩系数、最大可用升力系数和升阻比的角度，对翼型进行选择。统计国内外同级别无人机数据，其雷诺数大致都在2×105～4×105之间，本文取Re=2.5×105计算。权衡以上三项指标，最终选取S3010翼型作为该无人机的设计翼型。

机翼平面形状采取常规的梯形翼，带尖削、后掠和几何扭转。尖削为了使升力分布尽可能接近椭圆分布，从而减小无人机的诱导阻力。机翼后掠和几何扭转是为了减小纵向配平时升阻比的损失，但同时它会造成最大升力系数的损失，后面通过优化设计权衡和协调，使这种损失达到最低。

2.4 螺旋桨滑流区影响

无人机在拉桨作用下，螺旋桨对气流做功，使桨盘后的滑流区气流加速，导致机翼摩擦阻力D0增大。经试验和理论计算验证，螺旋桨动量定理和能量方程，可以对滑流区速度进行预测［5］。结合螺旋桨动量定理与能量方程［6］，得到滑流区等效摩擦阻力系数

式中，CD0为正常情况下的摩阻系数;ω为摩阻增加系数;SP为受滑流区影响的机翼面积;S为机翼面积;V2为滑流区气流速度;T为螺旋桨拉力;Q为螺旋桨桨盘面积;ρ为空气密度。

计算可知螺旋桨滑流区使无人机巡航和盘旋阶段摩擦阻力增加了不到5%，最终对航时影响不到2%。受螺旋桨高转速大拉力影响，无人机在爬升阶段，机翼摩擦阻力增加了30%左右，但其增加的拉力值不足5%。所以，螺旋桨滑流区占机翼面积较小使得它对全机性能影响也较小。另外，考虑到手掷抛射无人机，拉进式螺旋桨不易于击中操作人员，更加安全，权衡考虑后，选取拉进式螺旋桨作为本文动力方案。

2.5 气动布局与CMARC分析

该无人机采用飞翼布局，中间布置有机身，用于装载电池、电调、电机、飞控板等设备;机翼后缘内侧布置襟翼，用于起降;外侧布置升降副翼，用于滚转和纵向稳定性控制;两侧有翼稍小翼在减小诱导阻力的同时，提供航向稳定性。翼稍小翼采用融合式、外倾、前缘后掠、尖削的布局。设计方法类似于垂尾的尾容量法［7］，统计同级别国外无人机数据后，取小翼尾容量系数为0.02。

本文采用CMARC进行全机气动性能计算，该软件具备很好的计算精度［8］。面元法求解的是无粘无旋流动条件下的拉普拉斯方程，无法求解粘性阻力，CMARC通过边界层分析，预测粘性阻力。结合总体设计，用CMARC对无人机建模，进行气动力和纵向稳定性分析，全机模型如图2所示。

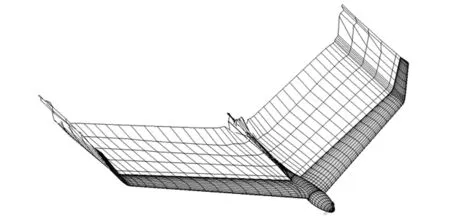
图2 CMARC全机模型和尾迹图

2.6 遗传算法优化设计

算例1的设计目标为无人机巡航时间t1、盘旋时间t2最大，总航时th=t1+t2;算例2的设计目标为无人机翼展b、重量W最小。设计变量包括机翼展弦比A;尖削比λw;四分之一弦线后掠角Λw;几何扭转角γ;襟翼展长占机翼展长的比例fs;襟翼弦长占当地机翼弦长的比例fc;襟翼距翼根的距离占机翼展长的比例k1;副翼展长占机翼展长的比例as;副翼弦长占当地机翼弦长的比例ac;副翼距翼稍的距离占机翼展长的比例k2;小翼前缘后掠角Λwl;小翼外倾角ψ和小翼尖削比λwl。另外，¯xc．g为无人机质心，¯xac为无人机气动中心，SM=¯xac－¯xc．g则为无人机的静安定裕度，令l=fs+as+k1+k2。两个算例优化模型分别为:

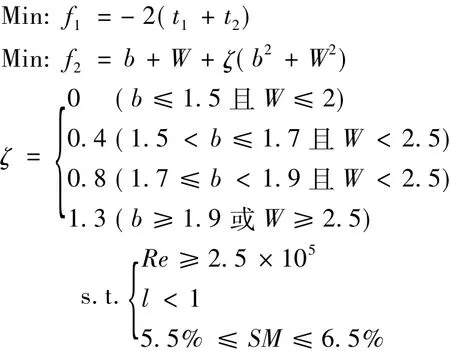
2.7 优化结果

遗传算法优化结果如表1所示。

表1 遗传算法优化结果

算例1总体设计计算结果如下:无人机巡航和盘旋总航时为3.88 h，起飞重量为1.962 kg，机翼面积为0.353 m2，翼展为1.73 m，所需最大推力为11.7 N，所需最大功率为 187 W，最大升阻比为25.7。

算例2总体设计计算结果如下:无人机起飞重量为2.182 kg，机翼面积为0.382 m2，翼展为1.85 m，电池容量为14.6 Ah，所需最大功率为205 W，所需最大推力为12.9 N，最大升阻比为26.5。

按照以上总体设计和优化方法，计算采用反弯度S5010翼型的无人机，与使用正弯度翼型的无人机对比。结果如表2所示。

表2 正、反弯度翼型无人机计算结果对比

算例1中，航时比采用反弯度翼型的无人机增加40 min，改善幅度达20%，同时无人机尺寸减小11%。由于电池容量固定，全机重量并未大幅度减小。

算例2中，相比于反弯度翼型的无人机，重量减小了37%，翼展减小27%，最大推力减小39%，电池容量减小42%。可见电池参与迭代后，全机重量得以大幅度改善。

3 参数分析

3.1 电池容量影响

对算例1，电池容量对无人机影响如图3所示。

图3 电池容量影响结果

由上图可以看出，电池容量变化对该模型航时和重量影响呈近似线性关系。当电池容量由10 Ah提升到15 Ah时(增加50%)，航时可提升近一个小时(增大33%)。

3.2 航时影响

对算例2，航时对无人机影响如图4所示。

图4 航时影响结果

当航时超过5 h时，飞机重量和电池容量会出现非线性增长。这是因为航时的增加导致电池重量增加，引起无人机重量增大，导致各个阶段所需功率显著变化。根据图1不同容量电池放电时间与所需功率变化关系，功率增加到一定值后，为达到额定的续航时间，电池重量激增，造成无人机重量及其它参数剧变。航时达到6 h时，无人机重量达到4.9 kg，最大推力接近30 N，此时螺旋桨以及整个动力系统效率非常低，势必消耗更多的电池能量，起飞重量比理论值更高。航时由4 h开始降低时，飞机的重量和电池容量也都相应减小，但减小量远不如增加的多。故对此类无人机最大航时以限定在4～5 h为最佳。

4 结论

通过对飞翼布局电动无人机的设计、优化和分析得到以下结论:

(1)对于飞翼式小型手掷电动无人机，采用正弯度翼型，可以得到相对于反弯度翼型更大的翼载荷和更高的升阻比，最终减小无人机重量和尺寸，降低手掷起飞速度，增大留空时间;

(2)电池容量对此类电动无人机航时和重量影响呈现近似于线性的关系;

(3)由于所需功率和电池容量对电池放电时间影响的限制，导致航时若超过临界值时，会使无人机各方面参数剧增，此临界点即为设计最佳点。

［1］李为吉．飞机总体设计［M］．第1版．西安:西北工业大学出版社，2004:8-10．

［2］Wagner N，Boland S．Power train design for hand-launchable long endurance unmanned aerial vehicles［R］．AIAA-2011-6047，2011．

［3］Lance W Traub．Range and endurance estimates for battery-powered aircraft［J］．Journal of Aircraft，2011，48(2):703-707．

［4］刘斌，马晓平，王和平，等．小型电动无人机总体参数设计方法研究［J］．西北工业大学学报，2005，23(3):396-400．

［5］Sergey Shkarayev，Jean-Marc Moschetta，Boris Bataille．Aerodynamic design of micro air vehicle for vertical flight［J］．Journal of Aircraft，2008，45(5):1715-1724．

［6］刘沛清．空气螺旋桨理论及其应用［M］．第1版．北京:北京航空航天大学出版社，2006:56-57．

［7］Ray mer D P．Aircraft design:a conceptual approach［M］．USA:AIAA Education Series，2006:121-122．

［8］Garrison P，Pinella D．CMARC user’s guide［Z］．Los Angeles:Aerologic Inc．，1996．