质量矩控制自旋弹弹体性能分析

高长生，张研，魏鹏鑫，荆武兴

(哈尔滨工业大学航天工程系，黑龙江哈尔滨150001)

0 引言

质量矩和舵是大气层内导弹的两种控制方式，与后者相比质量矩的优点［1-3］是:(1)气动外形良好;(2)抗烧蚀能力强［4］。缺点是:(1)内部需要活动部件，布局设计较难;(2)滑块运动引起惯性力大［5］。

前人通过研究得出惯性力及力矩对STT导弹弹体性能的影响很小，验证了惯性力及力矩在STT导弹上应用的可行性。而实现质量矩技术在自旋弹上的应用存在很多难点问题［6］。不同于舵面很轻可以忽略其动态特性的舵控制导弹，质量块运动的动态特性不能忽略。为了提高控制系统跟踪制导指令的能力，活动质量块必须频繁往复运动，因而产生的惯性力将严重地影响着系统的动态品质，降低了系统的性能［7］。

本文研究了滑块运动产生的惯性力对自旋弹的影响问题。首先将惯性力进行分类;然后分析了每类惯性力产生机理;最后研究了如何降低惯性力的负面效应。

1 问题描述

本文所研究的质量矩控制自旋弹采用单滑块的控制方式，其布局构型如图1所示。飞行器由弹体B和径向滑块p组成，滑块p的导轨平行于弹体坐标系Oxbybzb的yb轴。对于舵控制导弹而言，舵面做与弹旋同频率的正弦偏转运动可以对旋转飞行器产生控制力，这里滑块也按正弦运动进行。已有文献研究该类运动时未考虑滑块惯性力对系统的影响，因而系统是可控的。实际系统中必须考虑惯性力的影响，本文研究发现，惯性力的存在使系统难以保持良好的弹体特性。

图1 质量矩基本构型图

通过仿真分析验证了惯性力对自旋弹的影响。图1中滑块导轨远离弹体质心，这是公开文献普遍应用的自旋弹研究对象。该对象的弹体姿态响应会出现发散的情况，其准迎角的响应情况如图2所示。准侧滑角响应情况也类似。

图2 滑块持续正弦运动时自旋弹姿态响应

图2说明当导弹的总体参数选择不当时，在气动力和伺服电机的共同作用下，导弹为非保守系统，其准迎角与侧滑角会出现发散现象。下面将分析产生这种发散现象的原因。

2 质量矩控制导弹惯性力分类

弹体B、滑块p和总系统S的质量之间的关系为:mS=mB+mp;定义滑块p的质量比为:μp=mp/mS。定义弹体相对于地面坐标系的角速度为ω1=［ωxωyωz］T，弹体质心的速度为 V1，滑块p在弹体内的位置矢量为:rbp=［lpδy0］T。其中，lp为滑块p的轴向坐标;δy为滑块p的横向偏移量。则系统质心在弹体内的位置矢量为:

定义R1为空气动力;GS为地球引力;MS为空气动力对弹体质心b的气动稳定力矩;Md为阻尼力矩。质量矩操纵力矩Mc为:

弹体对质心b的转动惯量矩阵为:

则飞行器质心运动和绕质心转动的动力学方程可表示为:

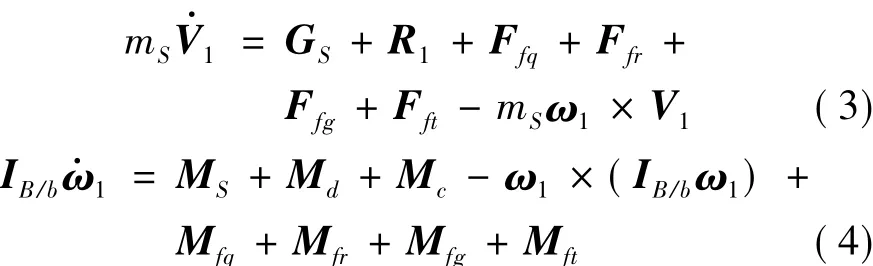
定义各个惯性力及惯性力矩如下:

(1)Ffr=为活动质量体伺服运动对弹体施加的反作用力，称为附加相对惯性力;

Mfr=－(rbp－rbs)×为Ffr对系统质心施加的作用力矩，称为附加相对惯性力矩。

(2)Ffq=

×rbp为由于弹体的角加速度运动，活动质量体对弹体施加的切向反作用力，称为附加切向惯性力;

Mfq= －(rbp－rbs)× rbp为 Ffq对系统质心施加的作用力矩，称为附加切向惯性力矩。

(3)Ffg=－2mpω1为由于活动质量体运动在弹体旋转角速度下对弹体施加的反作用力，称为附加哥氏惯性力;

Mfg=－(rbp－rbs)×(2mpω1×为 Ffg对系统质心施加的作用力矩，称为附加哥氏惯性力矩。

(4)Fft= －mp［ω1×(ω1×rbp)］为由于弹体姿态运动，活动质量体离心运动对弹体施加的反作用力，称为附加离心惯性力;

Mft= －(rbp－rbs)×mp［ω1×(ω1×rbp)］为 Fft对系统质心产生的作用力矩，称为附加陀螺惯性力矩。

3 惯性力对弹体性能的影响能力分析

设滑块的正弦运动规律为:

式中，A为滑块运动的最大位置;ωd为导弹自旋频率。则各个动态惯性力矩在准弹体系下的分量分别为:

其中:

通过数值仿真，将影响姿态运动各力矩在准弹体系下进行分解，图3给出了各力矩在准弹体系y轴上的分量。从图中可以看出，在俯仰方向上，各动态力矩虽然呈周期性变化，但并不是所有的动态力矩的周期平均力矩均为零，系统总惯性力矩均值也不为零。各个动态力矩均值(单位为N·m)为

其中，Msw和Mfq的平均力矩较小，与其它力矩相比可忽略。Mfr，Mfg和Mfw的周期平均值都要大于操纵力矩 Mc。

仿真结果表明:(1)惯性力是影响自旋弹弹体特性的主要因素，当动态惯性力矩平均效果大于系统操纵力矩时，系统将会出现发散现象;(2)由于该分析是针对典型布局形式开展工作的，因此结果具有一定的普遍性;(3)解决惯性力的负面影响问题，首先是优化弹体内部结构布局，降低该力的影响，在此基础上设计鲁棒性强的控制律。

图3 各动态力矩在y轴方向的分量

本文从总体布局角度分析如何降低惯性力的影响。为了使系统可控，必须消除各惯性力矩的平均效果。从式(6)～式(9)可知，取lp=0，即滑块导轨与弹体横向惯性主轴重合，在假设角速度分量ωy，ωz和ω·z为定值时，各动态惯性力矩在一个周期内的平均力矩表达式为:

由式(10)～式(13)可知，当lp=0时，各惯性力矩对导弹俯仰和偏航姿态的平均效果为零。这种情况下，质量矩控制的平均效果是由气动操纵力矩来产生的，这与STT导弹的质量矩控制原理类似。此时系统的姿态响应如图4所示。

图4 惯性力影响较小时弹体姿态响应

从图中可以看出，当滑块导轨与弹体横向惯性主轴重合时，可以减小惯性力矩对自旋弹姿态的影响，使得飞行器的姿态变化为一个稳态的响应过程。滑块的等效运动会产生一个弹体需要的准侧滑角。

4 结束语

本文研究表明:切向惯性力和离心惯性力的变化导致导弹惯性主轴频繁偏移;导弹自旋一周后哥氏惯性力和相对惯性力对弹体的等效控制力不为零，它们是影响系统性能的重要因素。

惯性力是影响质量矩在自旋弹应用的难点问题，其大小与导弹总体参数密切相关，为了降低惯性力的影响，提高系统控制能力，应该深入研究导弹总体布局问题。降低滑块导轨与导弹横向惯性主轴之间的距离可有效降低惯性力对系统的影响。当然，完全降低惯性力的负面影响是不可能的，还应从控制角度进行研究。本文从消除惯性力负面影响的角度进行研究，若充分利用总体设计技术，从利用惯性力正面影响角度去研究也是一种途径，这也是今后的努力方向。

［1］Kumar K D，Zou A M．Attitude control of miniature satellites using moving masses［C］//SpaceOps 2010 Conference．Huntsville，Alabama，April 25-30，2010．

［2］Mukherjee R M，Balaram J．Attitude dynamics and control of moving mass multi body aeromaneuver vehicle［C］//Atmospheric Flight Mechanics Conference and Exhibit．Honolulu，Hawaii，August18-21，2008．

［3］Vaddi SS，Menon P K，Sweriduk G D．Multi stepping approach to finite-interval missile integraed control［J］．Journal of Guidance，Control，and Dynamics，2006，29(4):1015-1019．

［4］Menon PK，Sweriduk G D，Ohlmeyer E J，etal．Integrated guidance and control of moving-mass actuated kinetic warheads［J］．Journal of Guidance，Control，and Dynamics，2004，27(1):118-126．

［5］李瑞康，高长生，荆武兴，等．飞行器变质心控制及性能分析［J］．宇航学报，2010，31(9):2165-2171．

［6］Yam Y，Mingori D L．Stability of a spinning axisym metric rocket with dissipative internal mass motion［J］．Journal of Guidance，Control，and Dynamics，1997，20(2):306-311．

［7］廖国宾，于本水，杨宇光．质量矩控制技术的机理分析及方程简化研究［J］．系统工程与电子技术，2004，26(11):1635-1639．