高超声速飞行器发射段运动模态特征分析

田霖，屈香菊，谭文倩

(北京航空航天大学航空科学与工程学院，北京100191)

0 引言

高超声速技术是当前各主要航空航天大国积极探讨与研发的关键技术之一。从军事方面看，运用这项技术开发的新一代武器系统将成为未来信息化战争的重要组成部分，该系统是具备战略、战术威慑力的空间作战平台，相关技术的研究应用于民用航空也将产生巨大的经济效益。

吸气式高超声速飞行器是高超声速研究的一个重要领域。该类飞行器的飞行任务剖面可分为3个阶段，即发射段、巡航段和下滑段。从飞行动力学研究角度来看，国内外相关工作主要集中在飞行器的建模以及巡航段定直平飞时的模态特征分析方面。与稳态巡航相比，飞行器在发射段的运动轨迹属于机动轨迹，其运动模态受基准运动状态的影响，可能产生新的运动模态。此外，由于目标飞行器在此阶段与助推火箭组成一个整体，其构型是非对称的，因此传统的纵横分开的线化模型不再适合于分析高超声速飞行器发射段的运动。

本文以美国X-43A飞行器在“飞马座”火箭助推下的发射段为背景，说明了整体飞行器在机动参考轨迹上线化模型的特殊性。同时，通过选取机动轨迹上的一个具有代表性的特征点，计算得出了飞行器在该特征点的运动模态特征，并对其形成机理进行了分析。

1 飞行轨迹特征分析

整体飞行器通过大型运输机挂载，经空中投放后，火箭点火并迅速跃升高度。该阶段属于发射段，此时整体飞行器的跃升过程见图1。

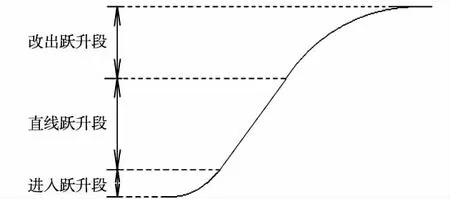
图1 发射段机动轨迹示意图

进入跃升后，飞行器通过增大迎角产生法向加速度，迅速将飞行姿态调整到一个较大的航迹倾角;飞行器在直线跃升段以固定的航迹倾角直线加速爬升;改出跃升时，飞行器迎角逐渐减小至负值，负的法向加速度使飞行轨迹逐渐改出为水平，保证吸气式飞行器与火箭分离时的平稳状态。由于改出跃升段的运动与常规飞行有较大差别，并且包含了整个机动轨迹上所有的运动特征，因此本文选择该段上的某特征点作为基准运动状态进行模态特征分析，并探讨其产生机理。

2 模型线化

根据飞行器六自由度一般运动方程，采用小扰动线性化理论，建立非对称构型、机动轨迹基准状态下的线化模型如式(1)所示，其中x=［V α q θH β p r φ］T为状态变量。

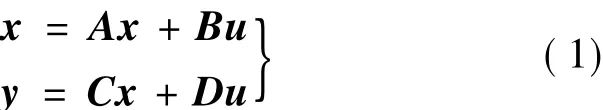
飞行器在发射段的机动轨迹属于加速运动，合外力不为零;由于运动轨迹弯曲，因此俯仰角速度不为零;并且在机动过程中高度、航迹倾角和迎角均不为零。另外，由于飞行器的构型不对称，因此其侧滑角也按不为零处理。

由于飞行器的基准运动是非定常的，其扰动运动方程为变系数微分方程，为便于数值求解，本文采用“系数冻结法”［1］，将变系数微分方程转变为常系数微分方程。由此可得状态矩阵A:

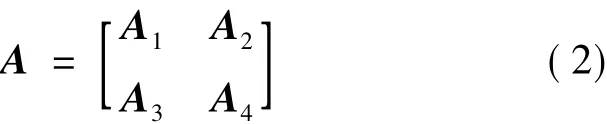
其中:

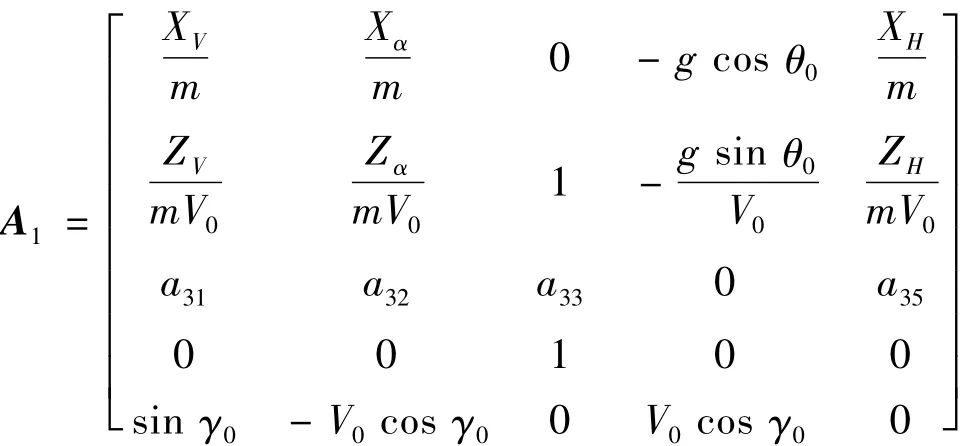
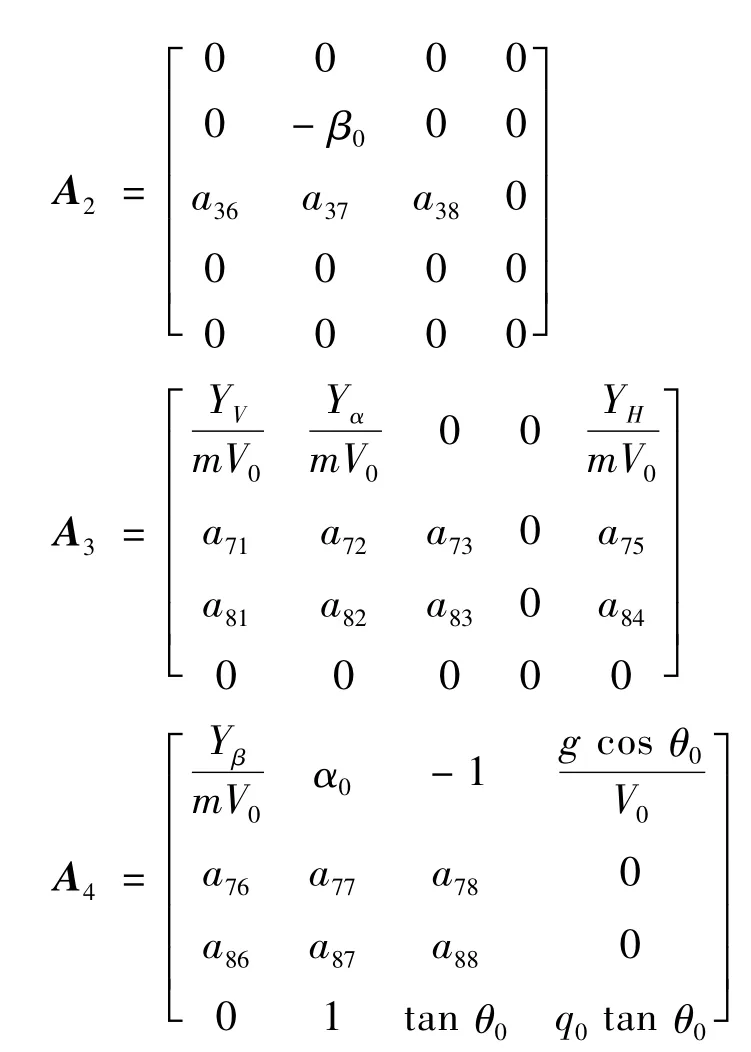
从状态矩阵可知，该飞行器在发射段与传统飞机巡航飞行的不同之处在于:

(1)飞行状态引起的变化。由于飞行器处于爬升高度的过程中，航迹倾角较大，力和力矩随高度变化明显;同时，机动轨迹上的俯仰角速度使得纵、横向的运动均受俯仰角速度的影响。

(2)飞行器构型不对称带来的耦合。飞行器的构型并不完全对称，由此也造成了纵、横向一定程度上的运动耦合。

3 模态特征

本文以X-43A与“飞马座”火箭构成的整体飞行器为研究对象，发射段的结构参数和特征点状态参数见文献［2-5］。通过采用相似构型的飞行器，估算特征点上的气动导数［6-8］，由此计算得到状态方程的特征根如图2所示。飞行器在该特征点处具有两个大的正实根和一对具有正实部的复根，说明飞行器运动不稳定。

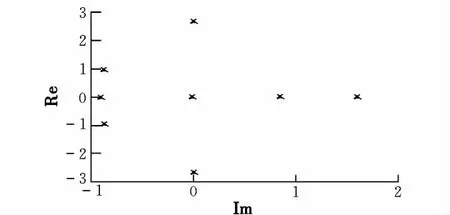
图2 特征根分布图

以特征向量实部作为状态变量的初值，对飞行器基准运动状态进行模态激励，从而确定各模态的主导运动变量，以便分析模态形成的机理。β0=－0.35°情况下的计算结果见图3～图8。

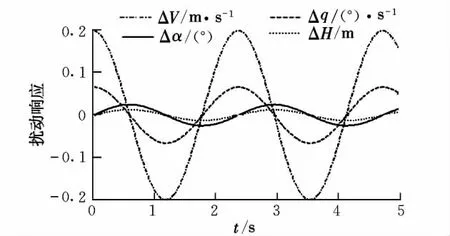
图3 纵向振荡模态激励曲线

图4 横侧向振荡模态激励曲线

图5 纵横向耦合振荡模态激励曲线

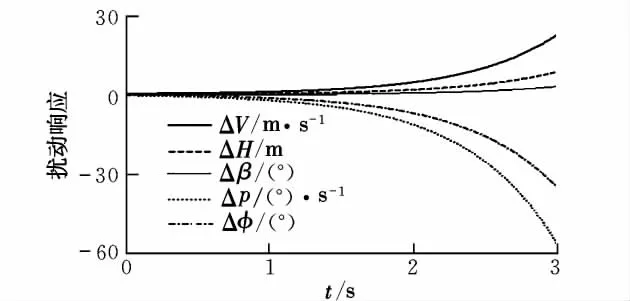
图6 滚转发散模态激励曲线

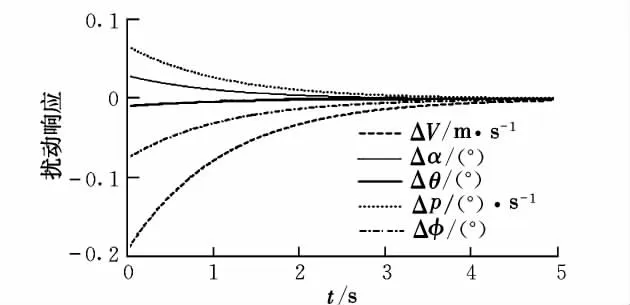
图7 纵向快变化模态一激励曲线

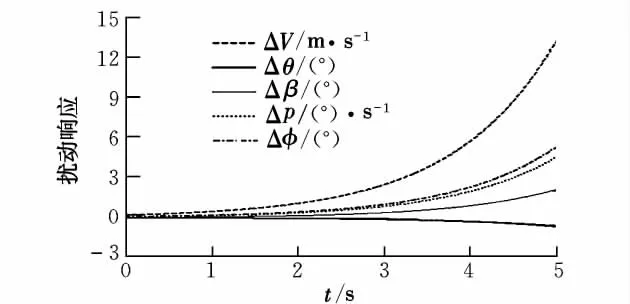
图8 纵向快变化模态二激励曲线

表1给出了飞行器模态特征分析结果。

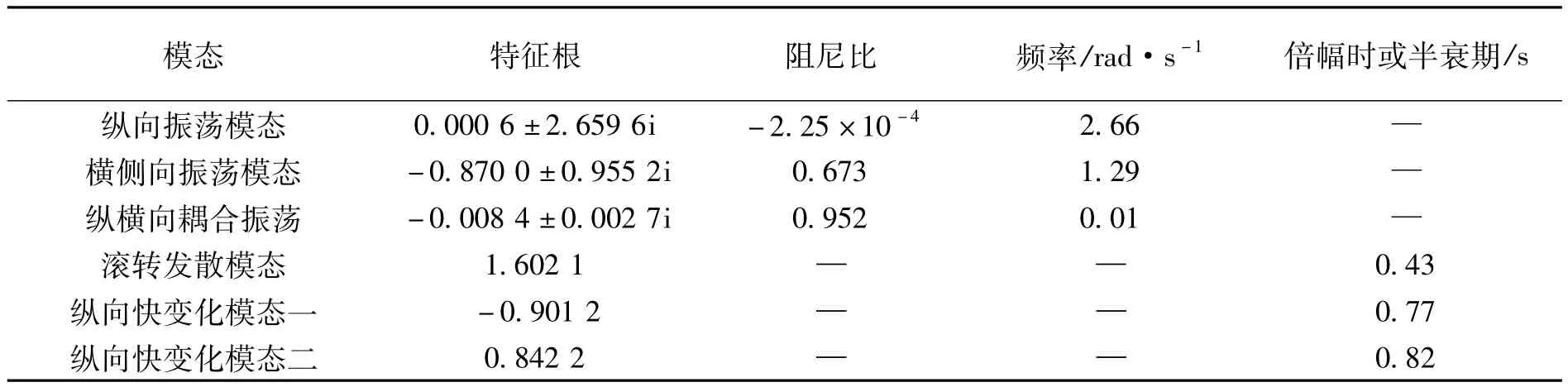
表1 飞行器特征点处模态特征

由以上计算结果可知:

(1)纵向存在一个频率较高的振荡模态，该模态阻尼很小，经长时间振荡后缓慢发散;横侧向也有一个较高频率的振荡模态，且该模态在纵向引起了一定的振荡;

(2)纵向另外的一个振荡模态衰减为一正一负的两个实根，对应纵向快变化模态一和二，这两个模态均在横侧引起了一定的振荡;

(3)横侧向存在一个大的正实根，对应滚转发散模态。从扰动响应曲线来看，这将使横侧向的滚转迅速发散，同时引起纵向长周期运动发散;

(4)纵向一个小根与横侧向一个小根相耦合，形成了一个纵横向耦合的振荡模态，该模态经长时间振荡后收敛。

飞行器纵向及横侧向的运动模态都呈现出了新的特点:纵向短周期运动阻尼很小，模态特性较差，而长周期运动则出现了单调收敛和发散两个新模态;横侧向滚转运动发散，荷兰滚模态特征不明显，同时，还有一个小根与纵向的一个小根耦合出了新的振荡模态;此外，纵、横向运动在很多模态均出现了一定程度的耦合现象。针对这些运动模态特征，下面将对其形成机理进行分析。

4 机理分析

对比稳态巡航，发射段的最大不同在于存在一个较大的航迹倾角，这对飞行器的影响主要有两个方面:首先，一个较大的γ值会使飞行器的受力与巡航时的情况大不相同;其次，由于γ值较大，力和力矩随高度的变化明显。

保持其它的飞行状态值不变，γ0依次取0°，3°，6°，9°，12°，可计算出飞行器各模态特征根的变化，如图9所示(其中(b)为(a)的局部放大图)。由计算结果可知，纵向的一个振荡模态在γ0增大到6°时衰减为一正一负两个实根;同时，横侧向的一个小的负实根和纵向的一个小的正实根耦合成一个振荡模态;其它运动模态受γ0值变化的影响不大。因此，航迹倾角主要影响飞行器长周期运动，对短周期运动影响不大。

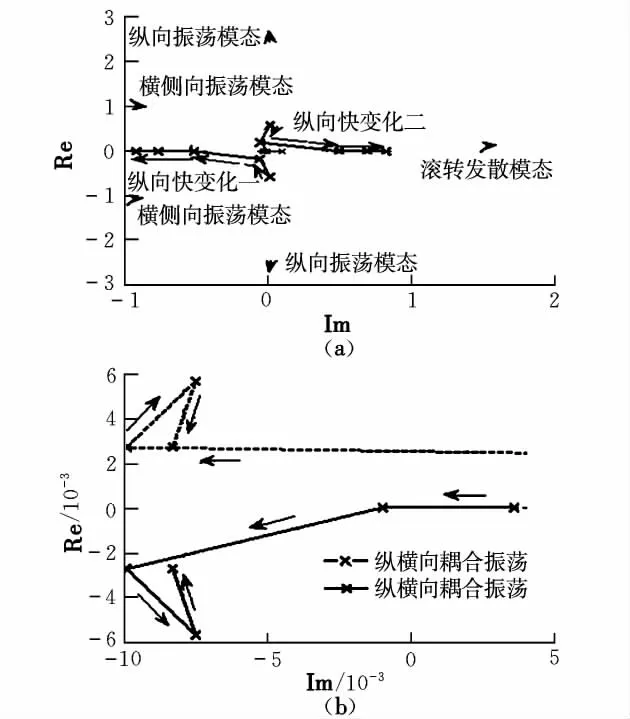
图9 特征根随航迹倾角的变化

飞行器在横侧向出现了一个具有大实根的滚转发散模态。要分析其形成机理，需从横侧向的运动方程入手。侧滑角的线化方程为:

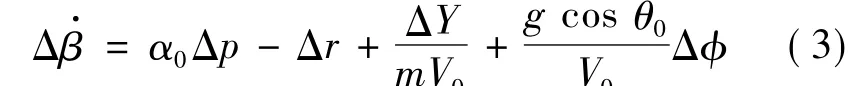
由于在特征点处α0＜0，假定飞行器受扰动产生 Δp＞0，则 Δβ·＜0，即 Δβ ＜0。而此时 Lβ＜0，由此产生附加的滚转力矩ΔL=LβΔβ＞0，使Δp·＞0，即Δp＞0。由分析可知，当基准运动状态为负迎角时，飞行器由于受到扰动产生的滚转角速度将进一步变大。在此过程中，如果滚转阻尼力矩不足以抑制这一趋势，将引起滚转发散。

若采用仅包含β和p的二阶模型(见式(3))，其特征根中包含了相应的不稳定大实根λ=1.156 8，由此验证了上面的分析。

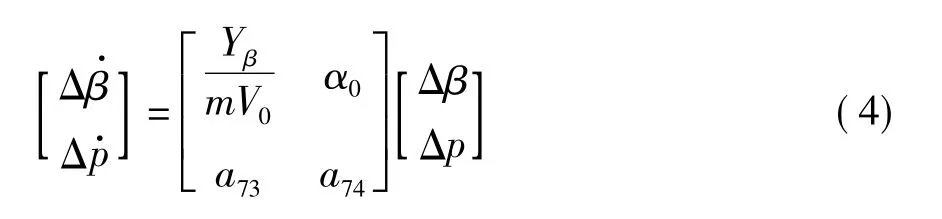
当α0为负时，其绝对值越大，由Δp引起的Δβ越大，从而产生的ΔL也越大，系统越不稳定;当Lβ越大，产生的ΔL也越大;α0和 Clβ取不同的值时，对应的横侧向实根值见表2和表3。通过计算，同样验证了以上分析。

表2 不同α0对应的横侧向实根值

由于飞行器构型不对称，基准运动轨迹上存在一定的β0，因此横侧向相关的气动参数不为零。根据第2节的分析，这将带来纵横向的运动耦合。取β0=－0.1°，计算结果如图10～图13所示。

图10 横侧向振荡模态激励曲线

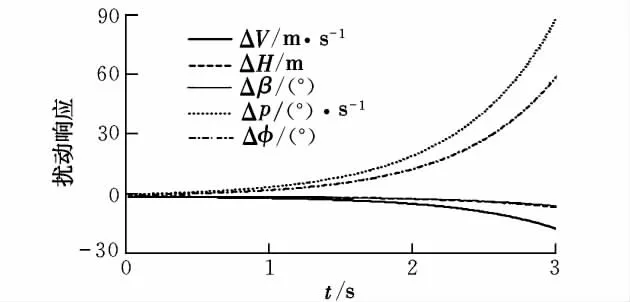
图11 滚转发散模态激励曲线

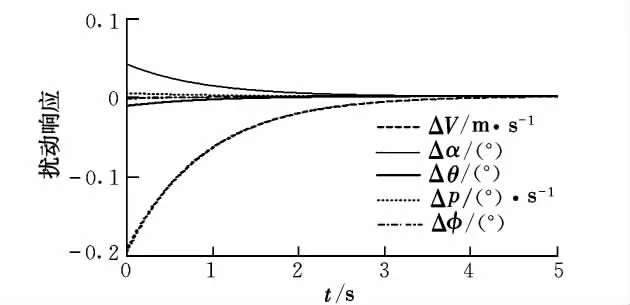
图12 纵向快变化模态一激励曲线

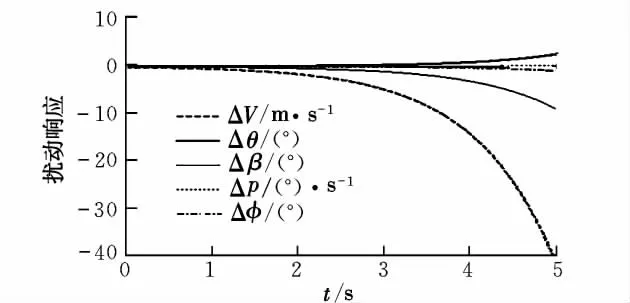
图13 纵向快变化模态二激励曲线

与之前β0=－0.35°时的模态激励曲线相比可知，|β0|越小，耦合程度也越小。可见，上述4个模态纵横向耦合的原因是飞行器构型不对称。

5 结论

(1)航迹倾角对飞行器长周期运动有较大影响。从计算结果看，当γ0较小时，传统的长周期模态仍能保持;当γ0≥6°时，长周期运动将出现新的特征，这将给控制系统设计带来新的问题。

(2)α及Lβ的共同作用影响横侧向滚转模态。在轨迹改出段，当α取值为负时，|α0|和|Lβ|越大，横侧向滚转发散越明显，飞行器也越不稳定。|α0|代表轨迹机动性，|Lβ|则由气动构型确定，这说明从控制器设计要求来说，需要综合考虑气动特性和轨迹选择。

(3)由飞行器构型不对称引起的β0使纵横向运动耦合。|β0|越大，耦合越明显，越难控制。

在实际应用中，考虑这些因素的影响对飞行器设计具有指导意义。例如在设计发射轨道时，直线跃升段航迹倾角不宜过大;俯仰改出时，负迎角也不应太大，即要求改出轨道变化不剧烈。

［1］方振平，陈万春，张曙光．航空飞行器飞行动力学［M］．北京:北京航空航天大学出版社，2005:174-193．

［2］Mark C Davis，Alexander G Sim，Matthew Rhode，et al．Wind-tunnel results of the B-52B with the X-43A stack［J］．Journal of Spacecraft and Rockets，2007，44(4):871-877．

［3］Paul V Tartabini，David M Bose，John DMcMinn，etal．Hyper-X stage separation trajectory validation studies［R］．AIAA-2003-5819，2003．

［4］Phillip J Joyce，John B Pomroy，Laurie Grindle．The hyper-X launch vehicle:challenges and design considerations for hypersonic flight testing［R］．AIAA-2005-3333，2005．

［5］Luat T Nguyen．X-43A flight 2 and 3 overview［R］．Salt Lake City，Utah:NASA Langley Research Center，2005．

［6］Shahriar Keshmiri，Richard Colgren，Maj Mirmirani．Development of an aerodynamic database for a generic hypersonic air vehicle［R］．AIAA-2005-6257，2005．

［7］Richard Colgren，Shahriar Keshmiri，Maj Mirmirani．Nonlinear ten-degree-of-freedom dynamics model of a generic hypersonic vehicle［J］．Journal of Aircraft，2009，46(3):800-813．

［8］Shahriar Keshmiri．Nonlinear and linear longitudinal and lateral-directional dynamical model of air-breathing hypersonic vehicle［R］．AIAA-2008-2531，2008．