基于动态逆的超低空空投抗侧风控制器设计
2013-08-09杨雨陆宇平戴正升
杨雨,陆宇平,戴正升
(南京航空航天大学自动化学院,江苏南京210016)
0 引言
大型运输机一般拥有非常大的翼展,且机翼有一定的下反角,使得飞机执行超低空空投任务时机翼相对于飞机质心距离地面更近。由于太阳照射等因素,低空气流相对于高空更加复杂,飞机易受到强侧风影响[1-3],一旦控制律不能对飞机的轨迹实施良好的控制,会使飞机偏离空投区域,错过空投机会,且姿态不稳定可能导致翼尖直接触地,致使飞机坠毁。理想飞行情况下,飞机执行超低空空投任务时横侧向应满足:(1)飞机地速与空投区域中心线方向一致;(2)飞机相对目标空投区域的侧向偏移为0;(3)机体轴与目标空投区域中心线方向一致;(4)飞机的滚转角为0°,以避免大翼展飞机翼尖触地。但多数情况下,飞机几乎不能在理想状况下飞行,因而在横侧向上对飞机姿态的要求也会改变,侧向偏离和航迹偏角应根据目标空投区域具体情况适当修改,在飞机进入空投段时可适当放宽偏航角来进行抗侧风控制,此外,考虑到空投区域地面可能会有起伏,且飞机高度并不稳定,所以需在横侧向留有一定余度,这将进一步减小飞机允许的最大滚转角。
飞机在正常的低空飞行和着陆的抗侧风控制律设计上已比较成熟,主要根据飞机的横侧向控制目的设计基于侧滑法和侧航法的横侧向控制系统,同时,针对可能提供直接侧力的控制面设计的直接侧力法,都取得了较好的控制效果[4-5]。
本文以超低空空投横侧向非线性模型及紊流模型为基础设计了PID控制器和横侧向抗侧风控制器,仿真结果表明,具有更理想的控制效果。
1 数学模型
分析飞机的动力学与运动学方程[6],结合飞机空投时的受力情况,可建立飞机横侧向数学模型如下:
当货物移动时,式(1)中:
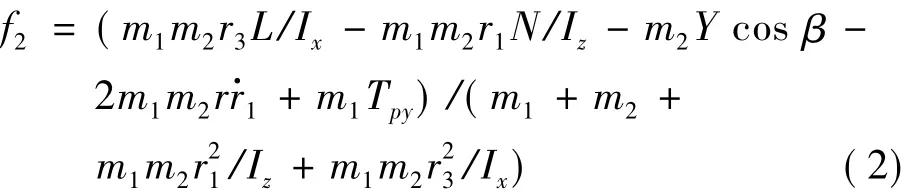
式中,m1为飞机自身质量;m2为货物质量;f2为货物对飞机的作用力在机体坐标系y轴的分量;r1,r3分别为货物质心相对飞机质心的位移在机体坐标系x轴和z轴的分量;Tpy为牵引伞拉力在机体坐标系y轴的分量。其它参数含义见文献[6]。
2 基于侧航法的PID控制器设计及仿真
2.1 控制器设计
横侧向飞行模态控制律设计均以飞机增稳系统为内回路,内回路结合侧滑法控制律,在副翼通道采用侧滑角反馈,方向舵通道采用侧滑角和偏航角速率的综合反馈,目的是改善横侧向飞行品质,以满足飞行品质中关于荷兰滚阻尼和频率、滚转模态时间常数和螺旋模态时间常数的要求,控制结构如图1所示。
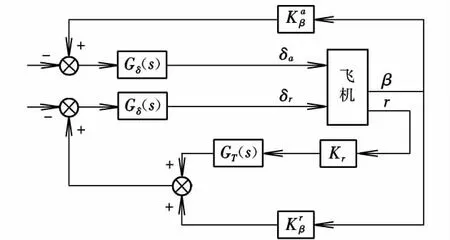
图1 内回路控制结构图
图中,Gδ(s)为舵机传递函数;GT(s)为清洗网络。此时控制律可以用下式表示:

以图1为内回路,利用滚转角反馈的PID控制,实现滚转角保持,控制结构如图2所示。

图2 滚转角保持控制结构图
最后侧向偏离的控制通过把滚转角保持回路作为内回路,通过PD控制来实现,为了保持空投过程的滚转角,在滚转角命令上加入饱和环节进行限制,其控制律结构如图3所示。

图3 外回路控制结构图
在方向舵通道不做任何改变,仍保持增稳回路。主要通过副翼通道控制飞机的侧向偏离,同时对滚转角指令进行限制,也限制了飞机的滚转角。
2.2 数值仿真
假设飞机重120 t,货物重20 t,飞行速度Ma=0.23。根据飞行品质设置横侧向增稳系统参数,令Gδ(s)=1/(10s+1),GT(s)=s/(s+1),Kaβ=1.117,。滚转角保持回路的PID控制参数设置为:Kpφ=15.7,Kiφ=0.35,Kdφ=16。在滚转角保持回路基础上设计侧向偏离回路,PD控制器参数选取为:Kpy=1.1,Kdy=4.2。
在模型中加入大气扰动来对横侧向控制系统抗侧风进行仿真。令侧向偏离指令为零,滚转角限制在±5°。飞机侧向偏离、滚转角、偏航角、侧滑角仿真曲线如图4所示。
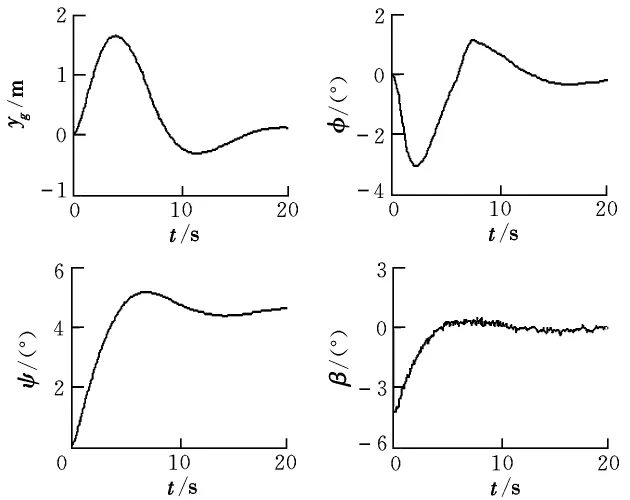
图4 仿真曲线
从图4中可以看出,飞机机头偏转了一个偏航角来抵抗侧风,滚转角和侧滑角都稳定到0°,滚转角最大偏转已经接近3°,侧向偏离也稳定到0 m。对比C-130对于超低空空投侧风的要求,6 m/s的侧风在超低空空投中属于较强的侧风,所以滚转角已经偏大。
系统的副翼和方向舵的输入曲线如图5所示。
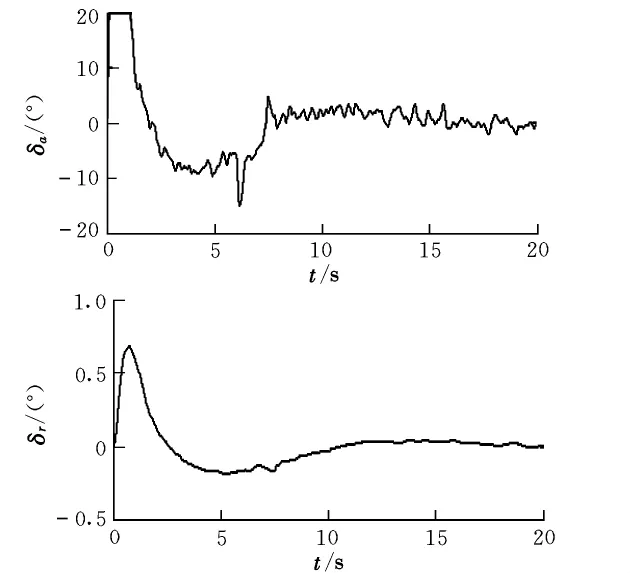
图5 舵面的输入曲线
由以上仿真结果可知,基于侧航法设计的控制律使飞机在横侧向紊流和常值风扰动下偏转一定的偏航角来对抗侧风,飞机的侧向位移和滚转角都能回到初值0,使飞机对准目标空投区域并保持飞机水平。需说明的是,以上仿真中飞机带货物并进行空投,所以完全可反映空投时飞机的真实飞行状态。从仿真曲线可以看出,基于侧航法对抗侧风时,副翼是主要的控制舵面,方向舵只是予以辅助,转动幅度很小。
3 基于动态逆的抗侧风控制器设计及仿真
基于侧航法对抗侧风时,主要利用了副翼通道,舵面偏转很大,且滚转角瞬时值偏大,下面设计一种基于最优调节器的动态逆控制器,在利用副翼的基础上,同时利用方向舵通道以减小滚转角的瞬时值。
3.1 横侧向模型的精确线性化
由于非线性系统不能像线性系统那样得到状态的解析表达式,在一定条件下通过状态和输入变量的适当变化实现所有或部分状态的线性化,从而将复杂的非线性控制系统设计问题转化为简单的线性系统设计问题。
为实现模型精确线性化,需利用非线性系统分析中的重要概念和运算符号:李导数和李括号,这将在后续的分析中大量应用,详细定义见文献[7]。
考虑输入输出维数相等的系统如下式:
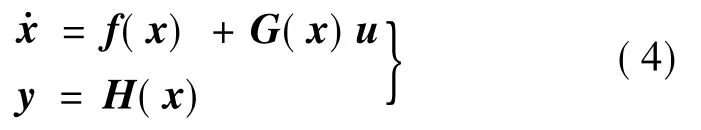
式中,x∈Rn,u∈Rm及y∈Rm分别为系统的状态向量、输入向量和输出向量;f(x)为n维充分光滑的向量场;G(x)=(g1(x),…,gm(x)),gi(i=1,…,m)为n维充分光滑的向量场;H(x)=(h1(x),…,hm(x)),hi(i=1,…,m)为充分光滑的标量函数。
对于非线性系统式(4),系统中第j个输出yj对时间的导数为:
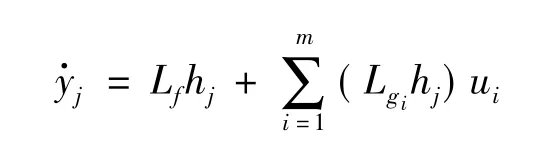
在上式中,如果所有Lgihj≡0,则导数与控制无关。若γj使导数 y(γj)j至少依赖一个输入的最小正数,即:
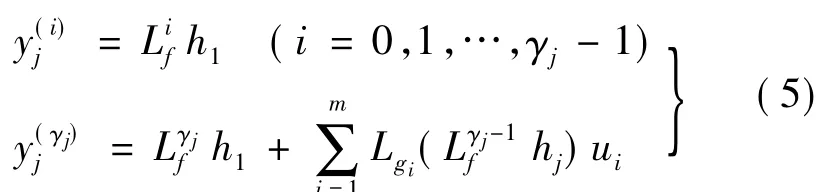
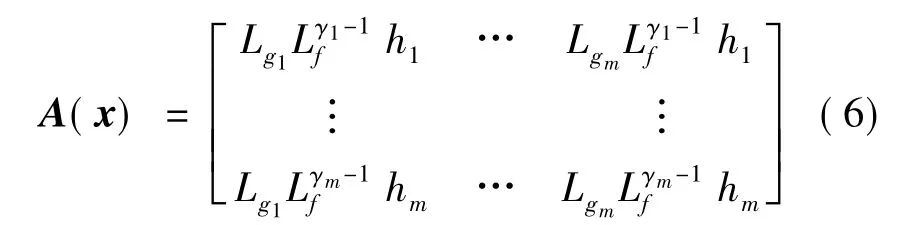
若如上定义的相对阶向量有定义,则式(5)可表示为:
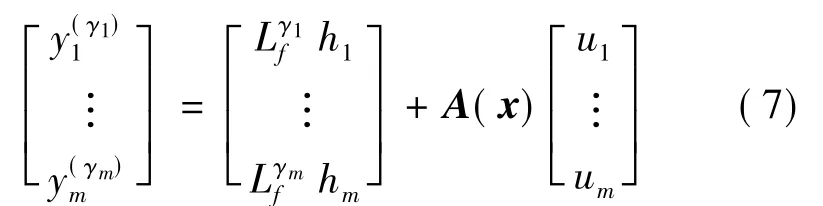
由于矩阵A(x)可逆,可取状态反馈控制律为:
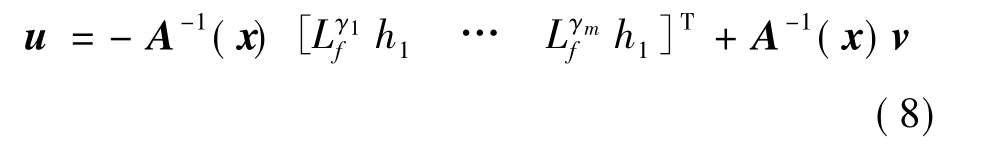
可以得到输入/输出的动态方程为:
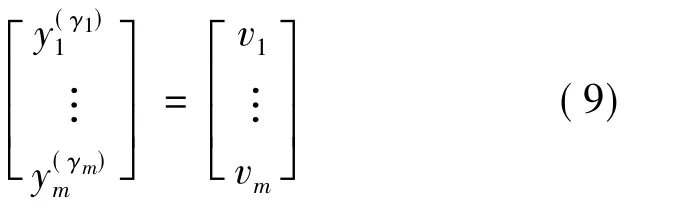
那么,通过输入/输出之间的精确线性化后所得的反馈表达式(9)就是原非线性系统式(4)的逆系统,如果将式(8)的输出看成式(7)的输入,可得到式(9),从而实现对非线性系统式(4)的动态逆控制[8]。同时,通过逆控制作用,还实现了对非线性系统的输入/输出解耦,因此矩阵A(x)也称为解耦矩阵。
从式(2)中可以看出,r·1,Tpy对于横侧向的影响有限,令r·1=Tpy=0。式(1)中,侧力 C、滚转力矩L、偏航力矩N可以通过相关的侧力导数、滚转力矩导数和偏航力矩导数计算。
把飞机横侧向模型化作式(4)的形式,可以得到:将各导数代入模型并展开可得到上式的各个量。
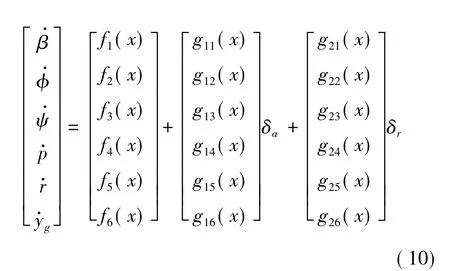
系统的输入只有升降舵和副翼,考虑到超低空空投时横侧向的控制目标,飞机滚转角和侧向偏离是决定空投能否成功的关键变量,所以把滚转角和侧向偏离作为输出进行输入/输出线性化。经计算:Lg1Lfh2≠0,Lg2Lfh2≠0,那么 γ2=1。同理可得 γ6=2。
代入式(7)得:
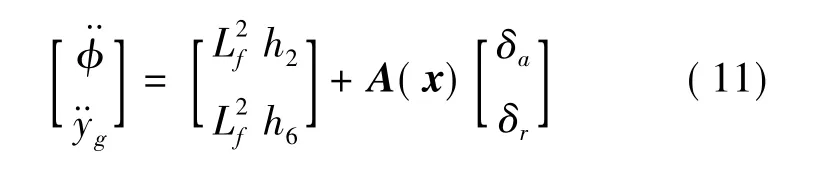
取状态反馈控制律为:
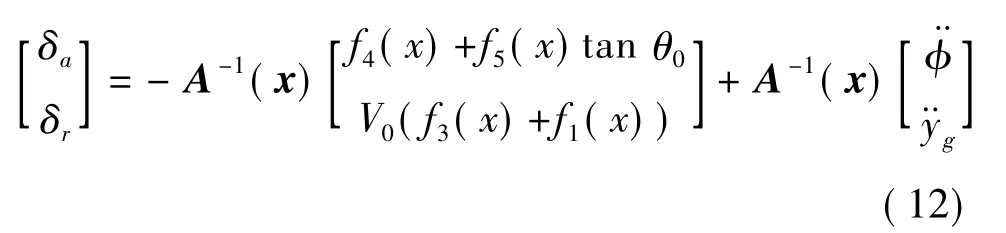
可以得到输入/输出的动态方程为:
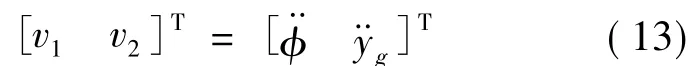
3.2 动态逆控制器设计
对横侧向定义向量 x=[x1,x2]T,其中:
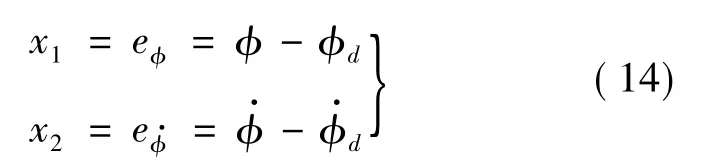
式中,φd为给定的滚转角值,控制目标为0。
对式(14)作微分运算,可得到:
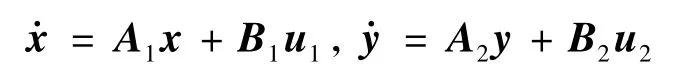
式中,u1=
那么,如果能够得到u1,u2的表达式,就可以得到动态逆控制器,考虑到便于计算和方便应用,使用最优状态调节器来求解,其表达式如下:
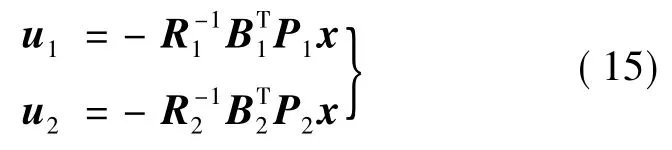
式中,矩阵P1,P2满足以下黎卡提矩阵方程;R1,R2为选定的正定对称矩阵。
那么控制器的输入可以表达为:
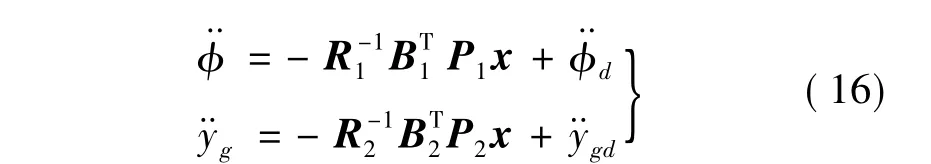
最后得到横侧向抗侧风动态逆控制律为:
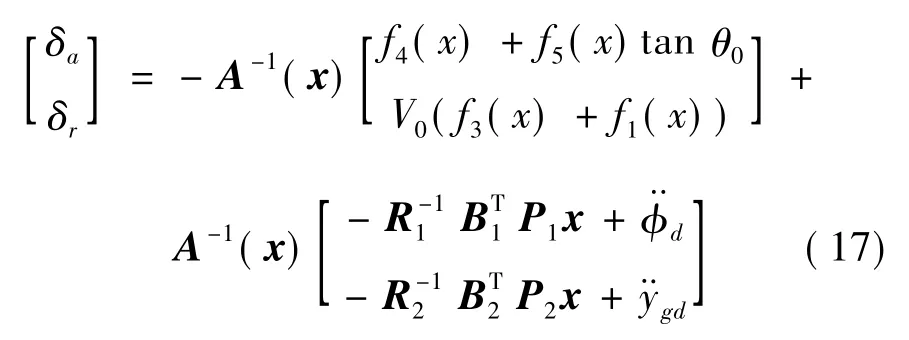
控制律结构如图6所示。
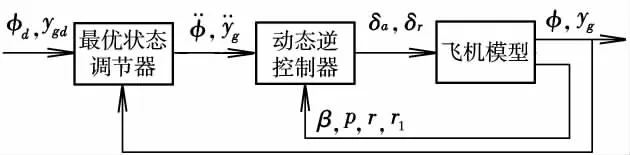
图6 动态逆控制器结构图
需要说明的是,系统需要货物的位置作为输入,这里把货物的位置设定为初始位置,如果货物的位置和速度都可以测量,则可以直接代入方程,如果不能测量,那么可以代入货物的初始位置,不做改变。
3.3 仿真结果
经过对飞机风洞数据分析和拟合,得到在h=5 m,Ma=0.23的状态飞行时,飞机横侧向气动导数如下:CYβ=-1.575 2,CY¯p=CY¯r=0,CYδr=-0.008,Clβ=-0.201,Cl¯p=-0.182 3,Cl¯r=-0.073 6,Clδr=-0.049,Clδa=0.001 1,Cnβ=-0.201,Cn¯p=0,Cn¯r= - 0.003 2,Cnδr= - 0.090 2,Cnδa=0。
飞机的转动惯量为:Ix=7 300 000 kg·m·s2,Iz=15 800 000 kg·m·s2,α0=θ0=1.022 6°。给定的滚转角和侧向偏离均为零。最优调节器的参数选取如下:
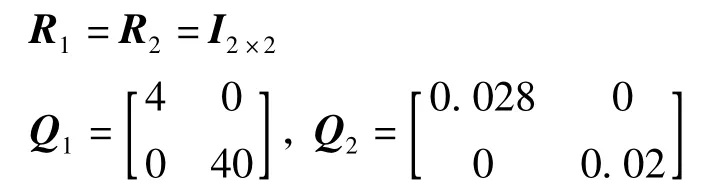
在大气扰动有紊流和6 m/s侧风的环境下进行仿真。仿真曲线如图7所示。
从图中可以看出,在相同的侧风干扰下,滚转角峰值几乎是侧航法的一半,原因在于系统的输入上,方向舵在有侧风干扰时也做出较大偏转来减小侧风的影响,同时系统能够很快达到稳定,而且对于紊流的抑制也表现出非常好的稳定性,有紊流干扰时,并不需要副翼来回偏转用以对抗紊流带来的影响。
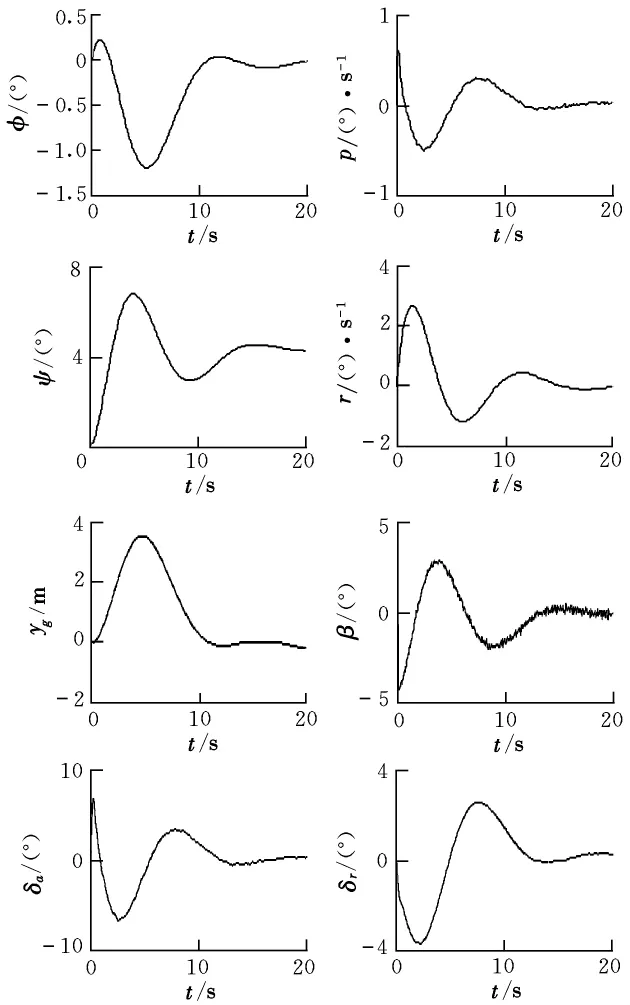
图7 仿真曲线
4 结束语
本文设计的两种控制器均能消除横侧向紊流及常值风影响,避免了因滚转角过大使飞机翼尖触地,确保货物顺利出舱,并使货物空投侧向偏离较小。而基于最优调节器的动态逆控制器比基于侧航法的PID控制器更能减小滚转角的幅值,且侧向偏离和偏航角能很快达到稳定,同时副翼不需要来回较大偏转,具有更好的控制效果。
[1]吕新波,张欣,刘振钦.农林飞机超低空飞行大气紊流影响研究[J].飞行力学,2008,26(2):64-68.
[2]张婧,陈澜,李晓曦,等.针对大气紊流改进的飞控系统设计及仿真研究[J].计算机测量与控制,2011,19(4):860-862.
[3]Blick M E.Effectof wind turbulence and shear on landing performance of jet transports[R].AIAA-78-20771,1978.
[4]王鹏,陈怀民,吴成富,等.飞翼无人机着陆过程中的抗侧风控制研究[J].计算机仿真,2009,26(12):78-81.
[5]嵇鼎毅,陆宇平.飞翼布局无人机抗侧风自动着陆控制[J].飞机设计,2007,27(2):25-33.
[6]吴森堂,费玉华.飞行控制系统[M].第1版.北京:北京航空航天大学出版社,2005:9-15.
[7]Lu Qiang,Sun Yuanzhang,Mei Shengwei.Nonlinear control systems and power system dynamics[M].Netherlands:Kluwer Academic Publishers,2001:38-45.
[8]Binh Dang Vu.Nonlinear dynamic inversion control[M].Berlin Heidelberg:Springer,1997:102-111.
