翼型弯度变化自适应规律研究
2020-12-08董彦非贺一帆
董彦非,贺一帆
(西安航空学院 飞行器学院,西安 710077)
0 引言
目前现役的固定翼飞机机翼的翼型在飞行过程中的弯度都是保持不变的。但是飞机高速和低速性能对机翼弯度要求相互矛盾,所以设计飞机时会对翼型的选择做一定的取舍,一般会选择在主要飞行条件下有较好升阻比的翼型[1],这样就导致飞机在主要飞行任务区之外的高度和速度范围内空气动力特性较差。
为了适应不同飞行条件对机翼弯度的要求,出现了变弯度机翼设计的方法。已有的变弯度技术主要集中在对机翼前后缘弯度的改变[2],还没有看到对翼型全面变弯度规律的研究文献。机翼翼型全尺寸变弯度技术目前还需要克服变体结构复杂、重量较大、蒙皮摩擦阻力大、承载能力差等问题[3-10]如果能实现机翼全面变弯度,会对飞机的飞行性能产生较大提升。
本文主要研究固定翼飞机随飞行速度和高度变化,机翼弯度对飞机升力和阻力特性的影响,通过计算分析得出不同速度和高度下最佳弯度自适应规律,为弯度自适应机翼设计提供基础。
1 弯度自适应规律研究
1.1 翼型的选取
机翼是为飞机提供升力的重要部件。翼型是机翼截面的基本构型,是指在机翼上与前缘垂直的剖面形状。翼型几何参数对飞机的气动特性和飞行性能有重要影响[11]。
自适应变弯度机翼对大型客机与运输机的空气动力特性提升较大,能够有效提高燃油经济性。这里选择典型的跨声速超临界的翼型DFVLRR-4。根据翼型原始外形数据计算得到中弧线之后,再对应计算出翼型的弯度与弯度相对位置。
为了研究翼型弯度和弯度相对位置所受影响,根据DFVLRR-4 翼型的数据,选择两组翼型进行CFD仿真。第一组对应改变弯度的相对位置,选择翼型:NACA2213,NACA2313,NACA2413,NACA2513,NACA2613,NACA2713,NACA2813。第二组进行扩展来观察弯度相对位置,选择翼型NACA4315,NACA4415,NACA4515,NACA4615,NACA4715,NACA4815,NACA4915。
1.2 建立翼型模型并生成网格
为了研究翼型弯度在不同来流速度、飞行高度条件下的空气动力特性,尤其是升阻力特性的变化规律,首先运用CATIA软件分别建立不同弯度的两组二维翼型模型,为之后进行的CFD仿真模拟计算做好准备。
通过流场相应的位置构建出相对应的离散点,然后通过这些离散点的组合总和成相应的网格[12]。网格的数量与质量会直接影响到CFD的数值模拟。
目前常用的网格有三种类型[13-14]:C型网格、O型网格和H型网格,本文主要采用C型网格,C型网格如图1所示。
对翼型处的网格进行加密,能更好地模拟边界层的空气流动,对向远场方向可进行一定倍率的放大减小网格数量以便后续计算,向远场方向可逐渐变稀[15]。优化以后调整网格结构使网格结构能够更接近矩形,因为计算的是二维翼型,结构都较为简单,网格质量应保证在0.9~1.0之间,优化后的网格质量如图2所示。

图1 C型网格

图2 优化后的网格质量
1.3 仿真条件设置
设置1000 m高度为起飞降落的环境,空气压力为89876.3 pa、温度281.651 K;选择5000 m和8000 m作为爬升和巡航条件。在5000 m的条件下空气密度和温度分别为54048.3 pa、255.676 K,8000 m的空气密度和温度条件分别是35651.6 pa 、236.215 K。
飞行速度Ma设定为0.1~0.8。因为Ma大于0.8以后翼型进入跨声速流场,此时的机翼表面存在局部超声速流,翼面上也会出现激波。
在超声速流动中,翼型弯度只产生阻力而不再提供升力。在超声速的时候尽量使翼型弯度为0(成为对称翼型)。
1.4 弯度影响分析
首先分析Ma对翼型的影响。对两组数据所计算得出的数据进行汇总并画出折线图,其中线条的数值对应着翼型的相对弯度值,第一组翼型的升力系数与Ma的关系如图3所示,第二组翼型的升力系数与Ma的关系如图4所示,其中每组图的迎角为0°、2°和4°时升力系数与Ma的关系。
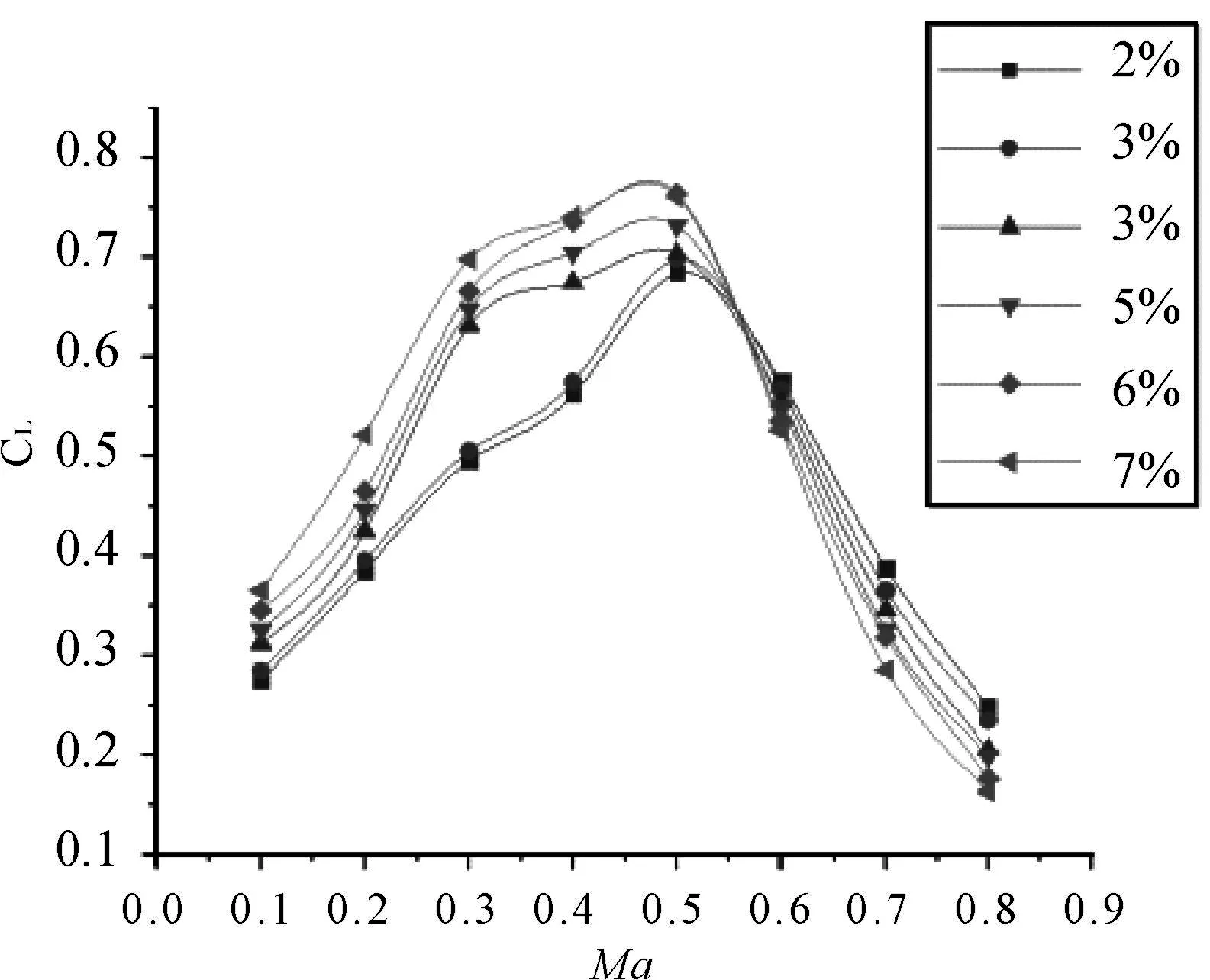
迎角为0°

迎角为2°

迎角为4°图3第一组翼型的升力系数与Ma的关系
从图3和图4中可看出,在Ma为0.1~0.4时翼型的升力系数为线性增长,并且弯度越大的翼型在此区间有着比其他弯度更大的升力系数。当Ma增大到0.5以后,弯度的影响出现了反作用,第一组数据在Ma=0.5~0.6时出现了交汇,第二组数据在Ma=0.6~0.7时样条线出现交会,从曲线图能看出,弯度较小的机翼在高Ma下有着优于弯度相对值较大的升力特性。
第二组翼型的阻力系数与Ma的关系如图5所示,由图5看出,阻力系数在Ma=0.1~0.4时增长都较为平缓,在Ma为0.5以后会出现较大增幅增长。因为随着Ma的不断增大翼型会出现气流分离,产生脱体涡从而使翼型的升力降低,阻力增大。
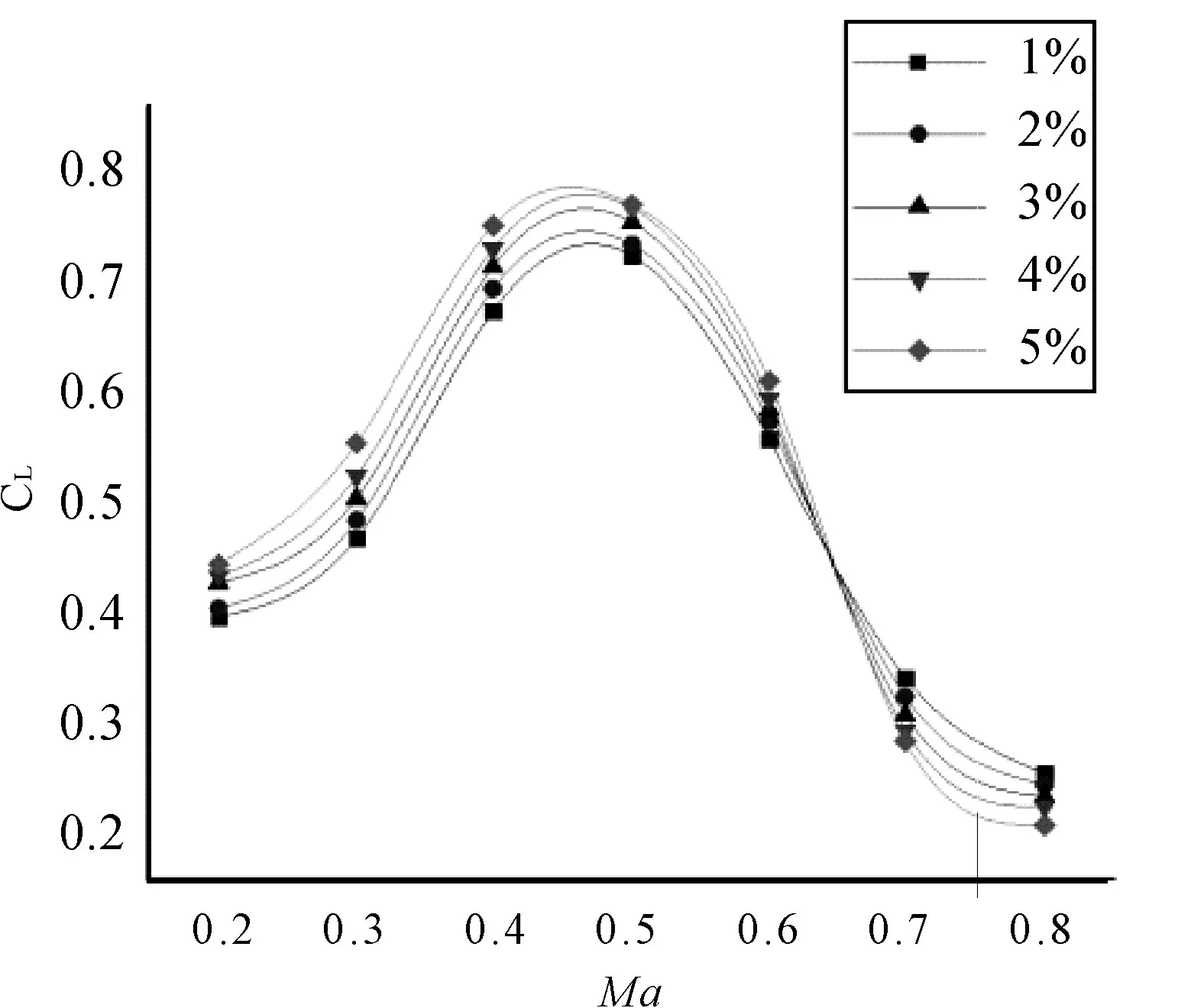
迎角为0°
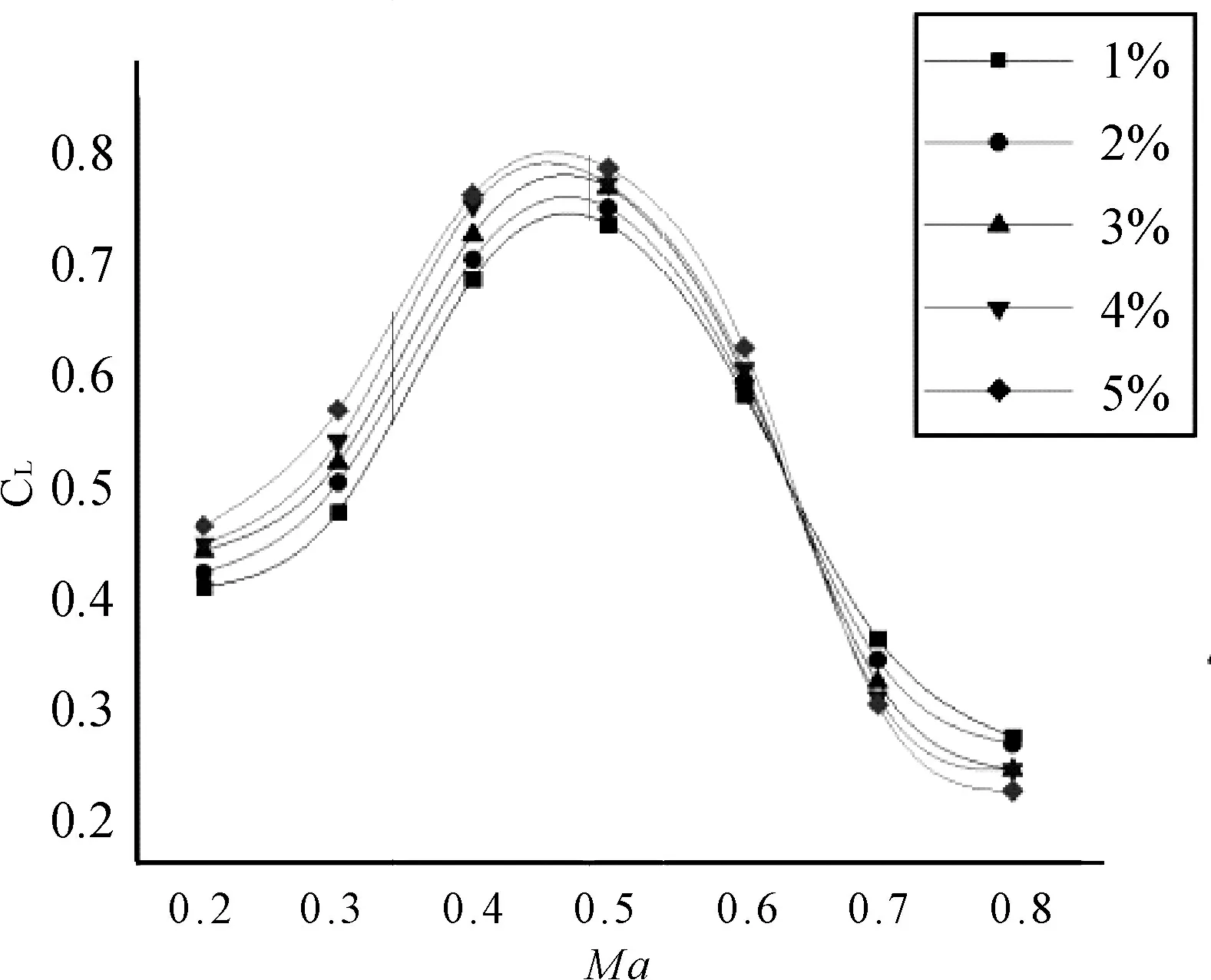
迎角为2°

迎角为4°

图4 第二组翼型的升力系数与Ma的关系
第二组机翼升阻比与Ma的关系如图6所示,结合图6可知,飞行过程中在Ma=0.1~0.4时升阻比近似于线性,在Ma为0.5左右时出现峰值,但增长率较低速时有明显下降。当Ma>0.5时翼型的升阻比出现明显下降。相对弯度较大时,低速飞行都有较好的升阻比,故在低速飞行时应当选择较大的弯度来作为此阶段飞行的弯度。当飞行速度在Ma=0.5~0.7时,弯度选择在3 %~5 %,当飞行速度Ma为0.8及以上时弯度应为1 %~2 %,当飞机进入超声速飞行时弯度应为0 %。
飞机在起飞着陆阶段会有较大的迎角产生,第二组翼型升力系数与迎角的关系如图7所示,由图7可知,升力系数随着迎角变化,因为在起飞和着陆阶段速度不会过大,所以只计算了较低Ma时角度对升力的影响。根据图7可知,迎角改变的大小对翼型弯度所产生升力的影响较小。
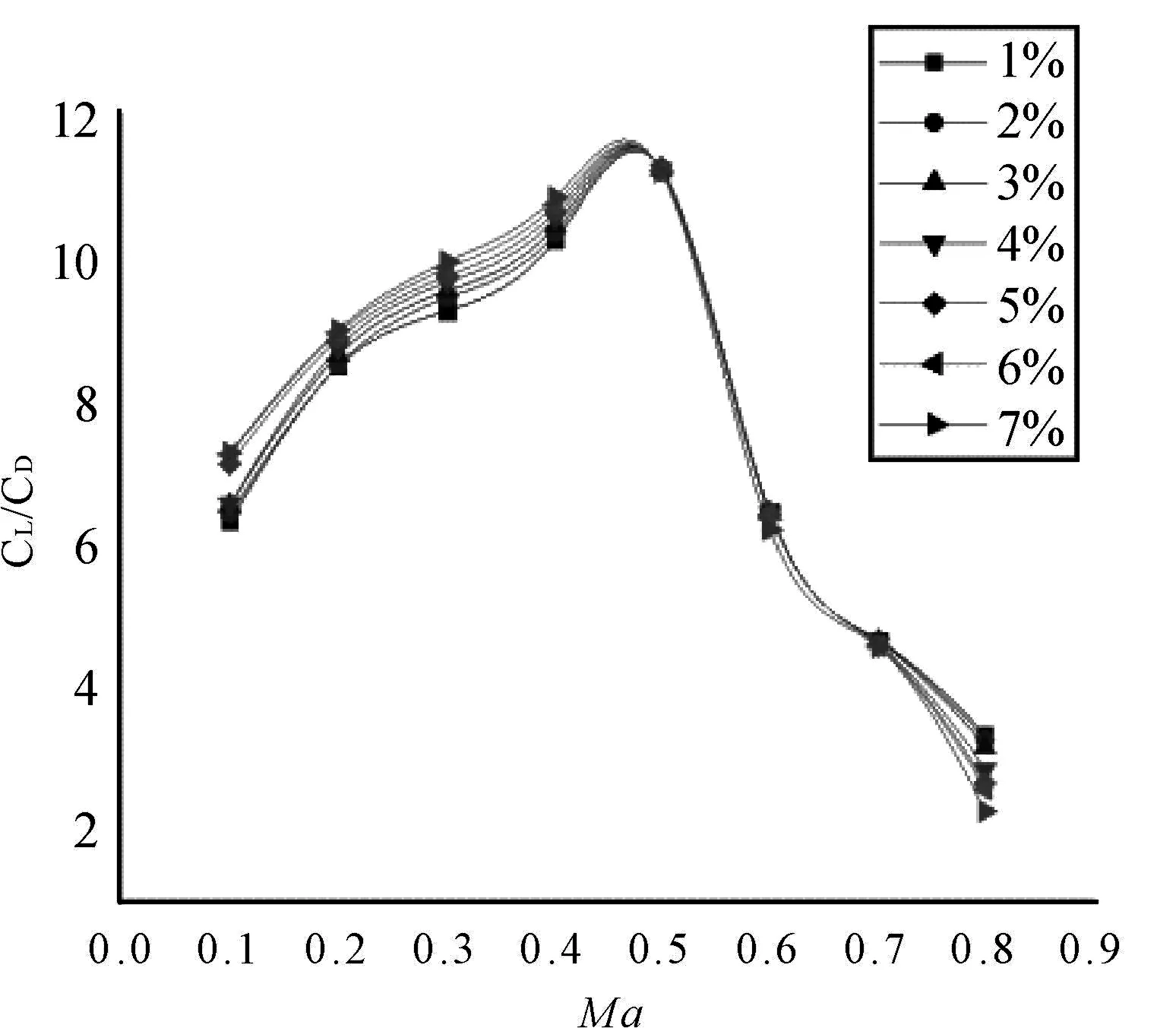
图6 第二组升阻比与Ma的关系

图7 第二组升力系数与迎角的关系
1.5 弯度相对位置的影响分析
第一组弯度相对位置对升力系数的影响如图8所示,第一组升阻比与Ma的关系如图9所示,第一组升阻比与迎角的关系如图10所示。结合图8、图9和图10的结果可以得出以下规律:弯度的相对位置越往后移动,下翼面的压力越大,从而导致上下翼面的压差增大,使机翼的升力增大。自适应变弯度机翼的弯度相对位置处于大于50 %时,虽然升力系数都会因为压差增大而增大,但机翼的阻力系数也会在迎角大于4°时出现激增,此时升力系数的增加量远小于阻力系数的增加量,从而使得机翼的升阻比急剧变小。所以当飞机进行小角度巡航时,弯度的相对位置后移较好,但当飞机做爬升时,弯度的相对位置会影响到升阻比,所以当飞机在爬升时应该将相对弯度的位置前移。

图8 第一组弯度相对位置对升力系数的影响
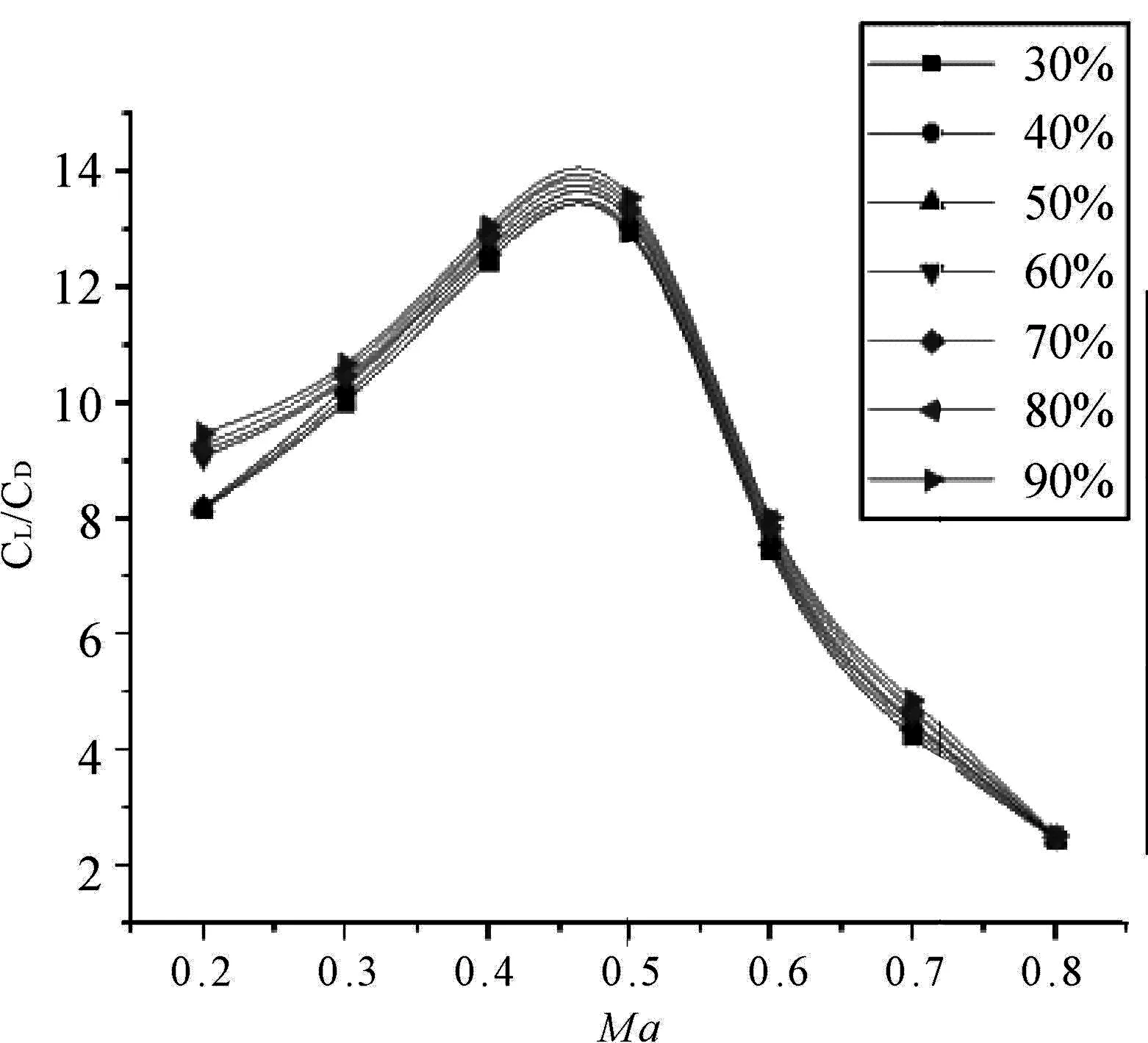
图9 第一组升阻比与Ma的关系

图10第一组升阻比与迎角的关系
1.6 飞行高度对翼型的影响
选择Ma为0.3和0.5进行计算,对得到的数据进行汇总,第一组翼型在Ma=0.3 时高度和升力系数的关系如图11,第一组翼型在Ma=0.5 时高度和升力系数的关系如图12所示。由图发现高度对升力没有明显的影响,因为飞行高度的增加,空气密度降低,温度也随着降低,所以升力系数也变小了。但随着高度的改变翼型的升力系数没有明显的交叠。通过目前有限的仿真结果分析未发现弯度变化对不同高度的机翼气动特性的影响。
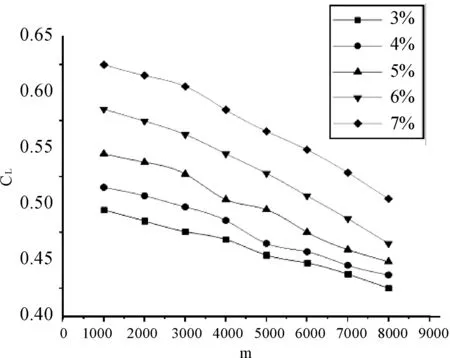
图11 第一组翼型在Ma=0.3 时高度和升力系数的关系
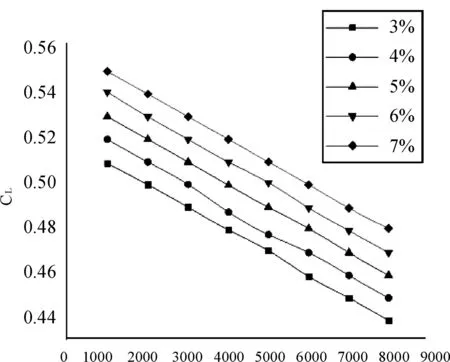
图12 第一组翼型在Ma=0.5 时高度和升力系数的关系
1.7 弯度自适应规律
对前面的数据进行汇总分析得到相对弯度值随Ma变化的建议区域图如图13所示,弯度相对位置随迎角变化的建议区域图如图14所示。用这两张图进行相对弯度与弯度的相对位置的建议。
图13中两条折线所包围的面积为自适应变弯度机翼在不同速度下建议的设计大小。上线为设计上限,下线为设计下限。两条线之间的阴影部分为指导区间,设计的自适应变弯度机翼的弯度大小在阴影部分就能获得一个较为优良的气动特性。图14其意义相同。
根据两张指导图给出自适应变弯度机翼的设计建议:自适应变弯度机翼设计在不同的飞行条件下保持弯度与弯度的相对位置在图中阴影区域时,都能有较为良好的升阻比。
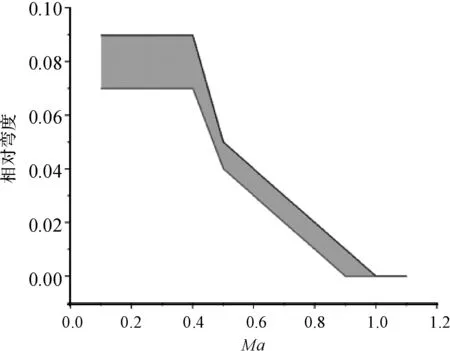
图13 相对弯度值随Ma变化的建议区域

图14 弯度相对位置随迎角变化的建议区域
2 结论
根据前面的仿真计算和分析,可以得到以下初步结论。
弯度变化的影响:
(1)当飞机处于小角度爬升和Ma小于0.5的飞行时,应采用7 %~9 %的翼型弯度,弯度对翼型带来的主要影响为增大最大升力系数使翼型的升阻比增大。
(2)当飞机的Ma超过0.5以后,此时仅仅增加弯度会使升力系数增大的同时也使阻力系数进一步增加。需要对升阻比的具体数值做对比,选择有较优升阻比的翼型,故弯度适当下降到3 %~5 %。
(3)当飞机在Ma为0.8以上时,由于出现了局部激波,使得弯度对阻力系数的影响进一步增大,所以弯度应该下降到1 %~2 %。
(4)当飞机进行超声速飞行时弯度在此时已不能起到产生升力的作用,弯度应变为0 % 。
对弯度相对位置影响:
(1)在做小角度爬升或巡航时,根据不同机翼的需求,翼型的弯度相对位置在70 %~90 %弦长位置的时候,升阻比有较大的提升。
(2)在做大迎角机动时,弯度的相对位置会使得阻力系数急剧增大导致升阻比降低。应在4°~8°时逐渐从60 %降低到20 %,在8°以后应继续前移弯度相对位置但要保持一定的前缘气动外形。
(3)在飞机进行超声速飞行时,弯度因为已经降低到0 %,故弯度的相对位置已经不对机翼的气动外形起到影响。
通过目前有限的仿真结果分析未发现弯度变化对不同高度的机翼气动特性的影响。
本文的计算结果和结论仅是在当前数据和计算条件下的初步分析,相关结论还需要进一步的大样本计算和风洞吹风等试验的支撑。
