波流作用下导管架码头结构浮运模拟数学模型及验证

李绍武，夏陆军，张文忠

(1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 中交天津港湾工程研究院有限公司，天津 300222)

波流作用下导管架码头结构浮运模拟数学模型及验证

李绍武1，夏陆军1，张文忠2

(1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 中交天津港湾工程研究院有限公司，天津 300222)

提出了一种导管架浮运稳定性数学模型．模型中，将导管架看作刚体，主要考虑波流荷载及拖缆对导管架的作用；依据刚体运动学相关理论，建立了导管架运动方程；波浪水流荷载用莫里森公式计算，控制方程采用4阶龙格-库塔方法进行求解．模拟了导管架浮运过程中波浪作用下6个自由度的位移响应和拖缆力，与水槽试验得到的拖缆力实测结果进行了对比，二者符合较好．对不同波浪入射角度和水流流向条件下导管架拖航情况进行了数值模拟，发现逆向入射30°浪的拖缆力最大，大于正逆向浪的情况．分析了缆绳与拖航方向的平衡角随横纵向流速比的变化趋势，得出比值越大，拖缆与航向的平衡角越大的结论．

导管架码头；莫里森方程；浮运；稳定性

导管架原本是浅海采油平台中一种常用结构型式，该结构具有刚度大，整体性好，所受波、流力小，以及对周围流场扰动小的特点，目前国外已有应用于开敞式码头的成功先例[1]．国内仅宝山钢铁码头曾进行过导管架码头结构的可行性论证[2]．

导管架一般采用陆上制造、海上安装的施工工艺．用于海洋采油平台的导管架结构一般体积十分庞大，重达数千吨至几万吨，直接浮运受近岸水深限制，往往采用驳船运到指定地点，再进行下水、定位、扶正和安放．此过程中，导管架由驳船下水的过程对于导管架施工安全至关重要，因此以往针对此方面的研究成果较多，如Jo等[3-4]借助SACS软件对导管架下水过程中受到的最大约束力、纵倾角、惯性力、下水轨迹以及驳船吃水等情况做了较详细的研究．Zhang等[5]根据前人研究成果，建立了导管架下水三维数学模型，其中考虑了风、浪、流因素．杨晓刚[6]利用MOSES软件模拟了文昌油田导管架吊装扶正过程，并分析了导管架吊装应注意的原则．He等[7]对导管架扶正进行了分析，通过在底部杆件设置小孔进行自由注水，实现了导管架的自扶正．

用于码头结构的导管架尺寸一般较小，所需浮运水深也较小，可以采用海上浮运的办法．由于拖航距离一般较长，导管架在拖航过程中的安全问题必须得到保障．笔者提出了一种数学模型，用来模拟导管架拖航过程中的运动状态，重点考虑导管架拖运过程中所受波、流荷载和拖航力，并用导管架物理模型试验中的拖缆力实测结果对数学模型进行验证．

1 数学模型

1.1 控制方程的建立

将导管架看成刚体，可以建立6个自由度的刚体运动方程[8]．建立如图1所示的固定和连体2套坐标系．固定系为Oξηζ，其原点为O，Oξ和Oη轴保持水平，与静水面重合，Oζ垂直于Oξη平面；连体坐标系Cxyz的原点C与导管架重心重合．

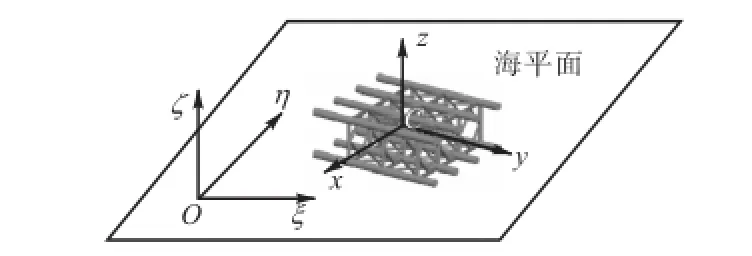
图1 坐标系Fig.1 Coordinate system

根据动量守恒原理，连体坐标系下导管架平移旋转方程为

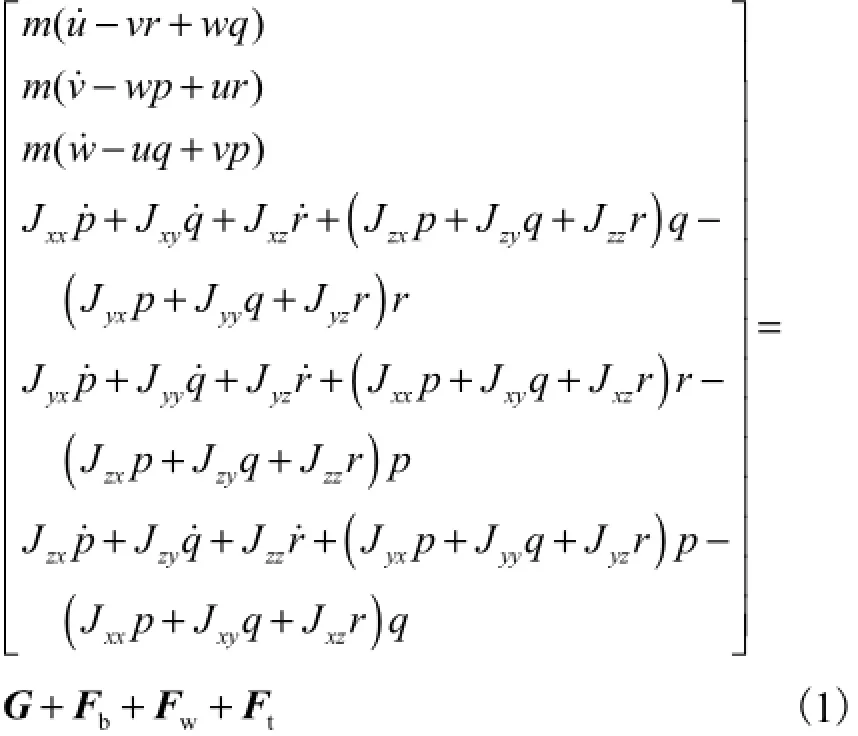
式中：m为导管架质量；(u，v，w)T和(p，q，r)T分别为导管架重心速度和角速度在连体坐标系下的投影；J为导管架惯性矩阵；G为重力；Fb为浮力；Fw为水动力；Ft为拖缆力．

根据坐标系的转换关系，可以得到固定系下角速度与连体坐标系间的关系为

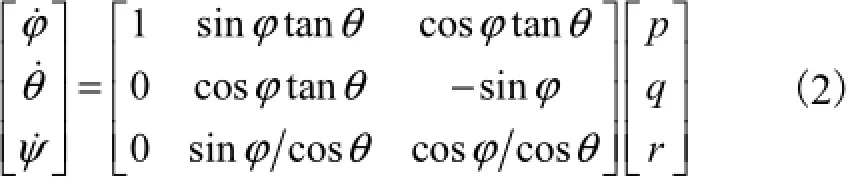
固定系与连体坐标系间重心线速度间的关系为

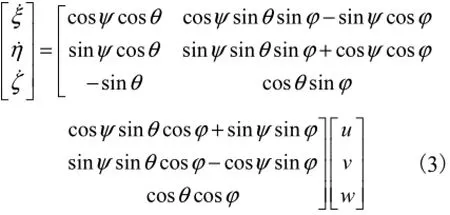
式中：φ、θ、ψ为姿态角；ξ、η、ζ为导管架重心位移．

式(1)～(3)共计12个方程且包含13个未知数(t，u，v，w，p，q，r，ξ，η，ζ，φ，θ，ψ)，考虑t是自变量，则构成封闭方程组，可以联立求解，但需给出导管架所受外力(矩)在连体坐标系下投影的表达式．

1.2 导管架所受外力

导管架所受外力(矩)包括重力、静水压力、水动力以及缆绳拉力．

1) 浮力

将导管架杆件看成细长型圆柱体，参照文献[9]计算导管架所受浮力．

2) 水动力

导管架是由小直径管柱组成的一种结构，可以用莫里森公式计算其水动力．针对每个圆柱型杆件建立杆件坐标系统(见图2)，将莫里森方程应用于该系统，杆件微段dl上所受作用力[10]为

式中：dFwx′、dFwy′分别为杆件微段dl所受波流力在杆件坐标系下x′、y′方向的投影；D为直径；uwx′、uwy′和awx′、awy′分别为dl处的水质点速度和加速度在x′、y′方向的投影；ulx′、uly′和alx′、aly′分别为杆件dl微段的速度和加速度在x′、y′方向的投影．

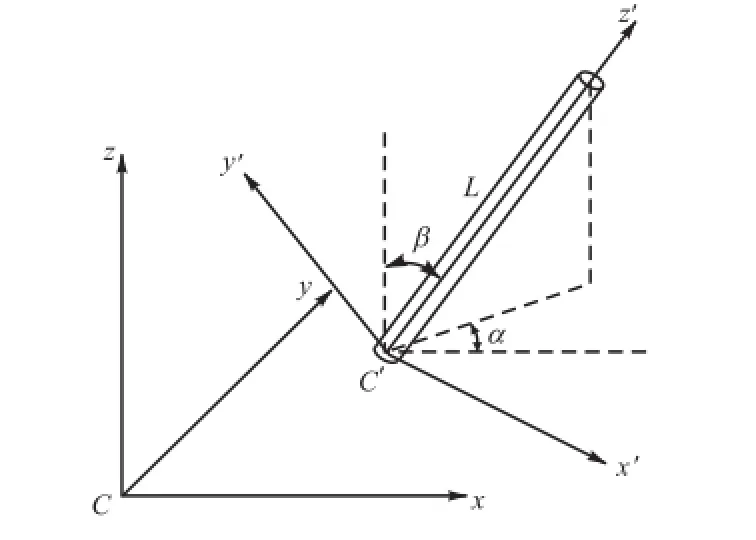
图2 杆件坐标系Fig.2 Bar element coordinate system

将水质点速度和加速度看作波浪场和水流场的叠加．波浪场水质点速度和加速度可以用线性波理论计算．杆件dl处的速度、加速度可表示为

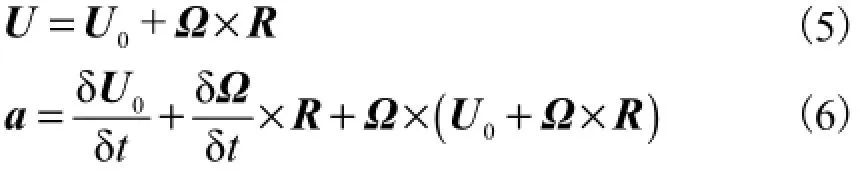
式中：U0为导管架重心速度；Ω为导管架角速度；R为dl处的点在连体坐标系下的坐标．

沿杆件长度方向积分，可得波浪和水流力计算式为式中：N为杆件坐标系和连体坐标系的转换矩阵；为导管架重心在杆件坐标系下的坐标；z′0为杆件没入水中的长度．

3) 拖缆力

假定缆绳一端系在导管架上，另一端以一定的速度U拖动向前，拖缆力按照Wilson公式计算，即

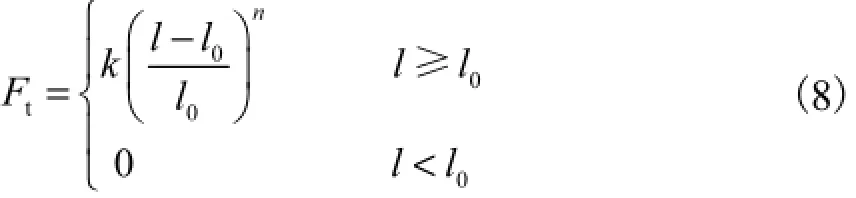
式中：k为系数；n为指数；l为缆绳瞬时长度；l0为缆绳张力等于0时的长度．

1.3 方程组的求解

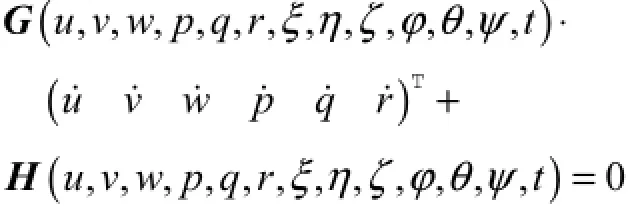
经线性变换，结合式(2)和式(3)，令yl=u、v、w、p、 q、r、ξ、η、ζ、φ、θ、ψ，l=1,…,12，则12个控制方程可以写为y˙l=fl(t,yj)(j=1,…,12)的形式．采用标准4阶龙格-库塔方法求解控制方程，方法为

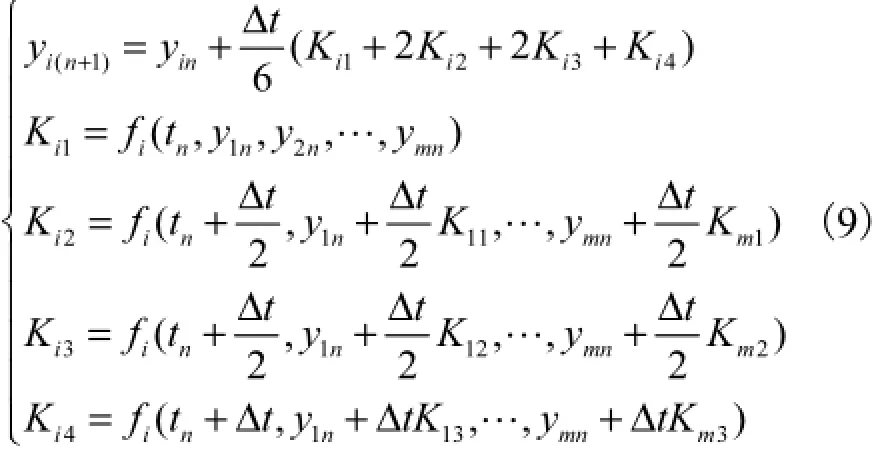
式中：i为迭代次数；12m=；tΔ为时间步长．

2 导管架模型算例

2.1 导管架自振特性模拟

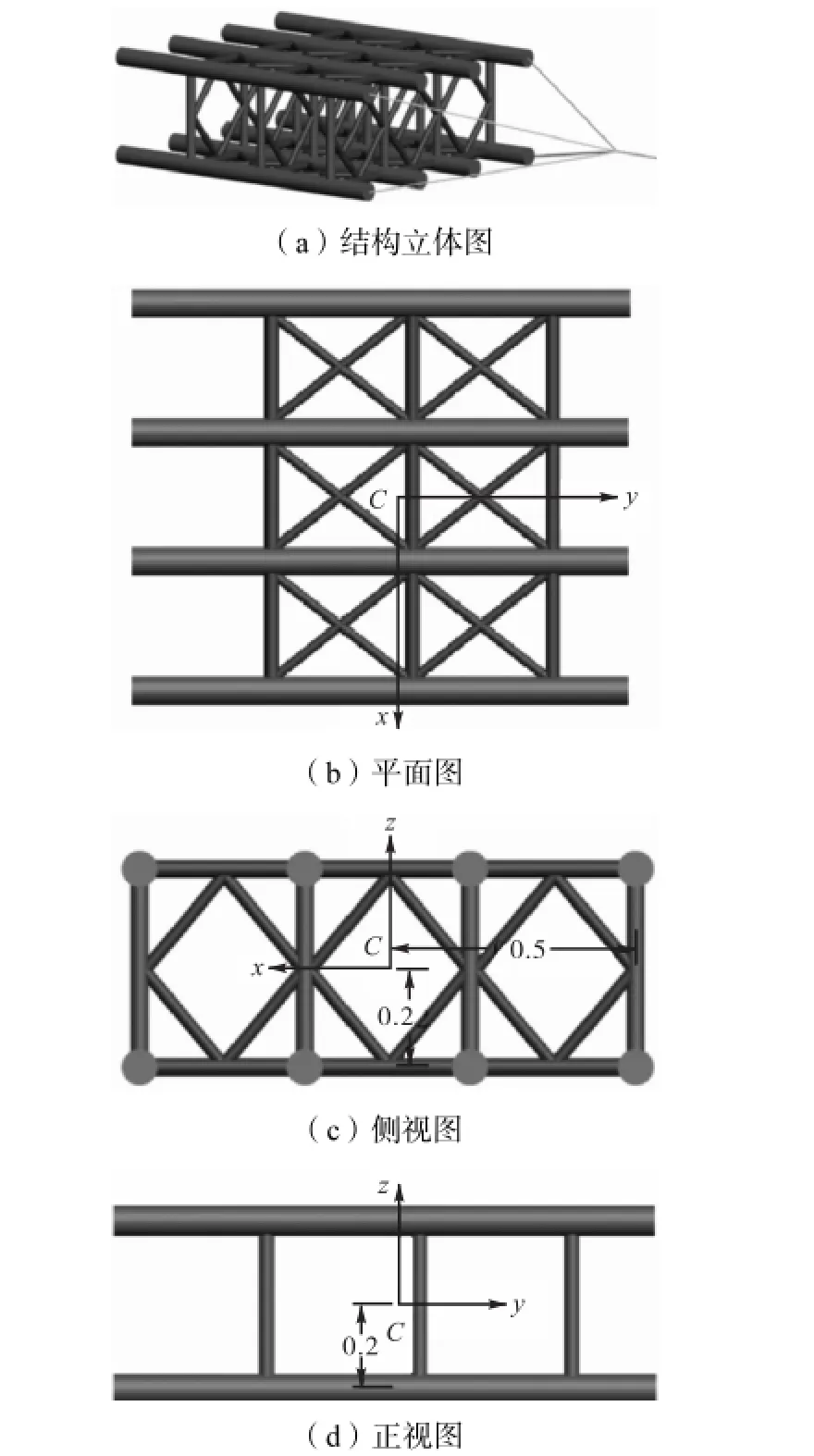
图3 导管架模型(单位：m)Fig.3 Jacket model(unit：m)

针对图3所示的导管架结构进行自振验算．导管架关于x、z轴对称，关于y轴不对称．横卧放置在水面的导管架(图3(a)的姿态），静止时，其重心位于水面以上0.154,m，初始纵摇角(φ角，绕x轴，右手法则下顺时针为正)为-5.27°．为测定导管架的垂向自振周期以及绕x轴的纵摇周期，分别使导管架在平衡条件下①沿z向向上提升8,cm，②绕x轴转动2.86°，导管架重心在z向的位移及纵摇角随时间变化计算结果分别如图4和图5所示．

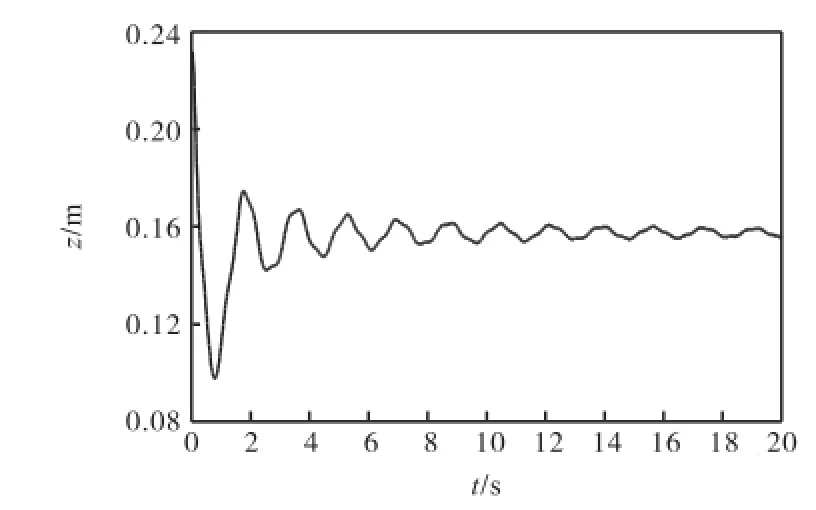
图4 导管架垂向自由振荡Fig.4 Vertical free oscillation of jacket model

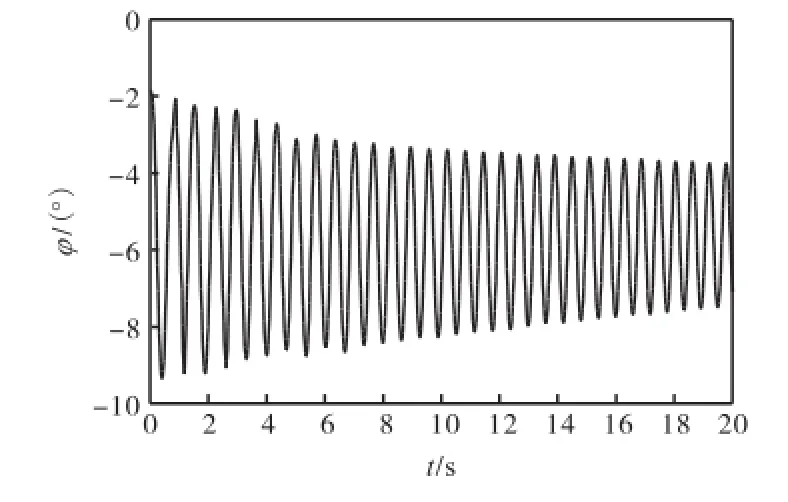
图5 导管架绕x轴(φ角)自由摇摆Fig.5 Free pitching of a jacket around x axis(angle φ)

可以看出，导管架垂荡周期为1.40,s，纵摇周期为0.58,s．导管架在水阻力的作用下垂向振幅迅速减小，而纵倾振幅衰减较慢．

2.2 导管架强迫振动特性模拟

按表1的波浪条件，计算导管架(与2.1节中尺寸相同)在波浪作用下的响应．最大振幅(在波浪作用下稳定后1个周期内的最大位移差)计算结果如图6和图7所示．波浪周期为0.58,s和1.4,s时导管架振幅均出现峰值，这与导管架的自振周期是一致的，说明发生了共振．

表1 试验波浪要素Tab.1 Wave conditions in experiments

2.3 拖缆力验证

2.3.1 拖航试验装置

为进一步检验数学模型的正确性，在水槽中进行了导管架物理模型试验，对拖缆力进行了测定．物理模型试验以上海宝钢马迹山30万吨级矿石中转码头工程中提出的导管架结构方案为原型，按照1∶30比例缩小后，采用不锈钢制作而成．模型试验由中交天津港湾工程研究院在波浪水槽(图8)中完成．采用台车通过钢丝缆拖航，导管架的4个主撑钢管各系一根0.96,m的钢缆，系结一处后，通过一根6,m长的主钢缆与台车相连．缆绳力采用环形测力计进行测量．共进行了3组试验，组次1、3为逆浪，组次2为顺浪．试验中，导管架在台车带动下由水槽的一端向另一端移动．导管架模型参数如表2所示，拖航试验参数如表3所示．

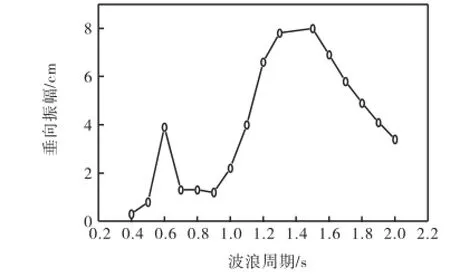
图6 导管架垂向振幅随周期变化Fig.6 Variation of vertical displacement amplitude of jacket with respect to wave period

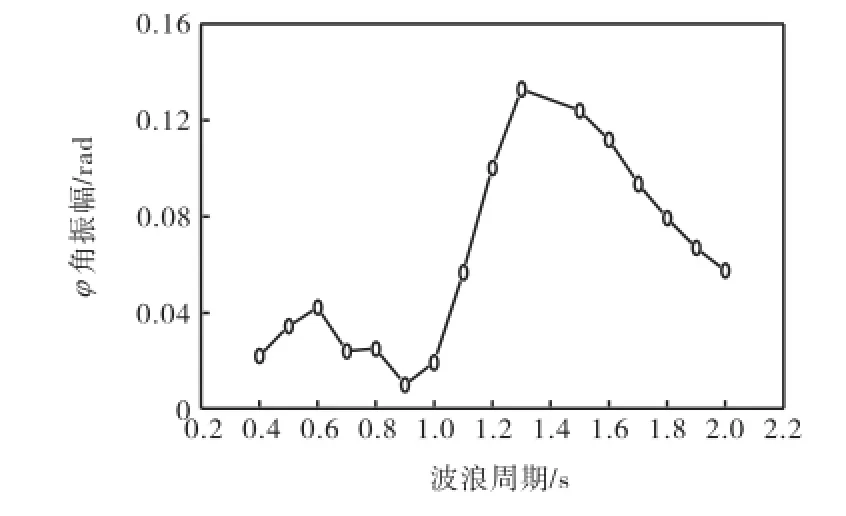
图7 导管架φ角振幅随周期变化Fig.7 Variation of amplitude of jacket with wave period

图8 导管架模型拖航试验Fig.8 Sketch and pictures of jacket model used in towing experiments

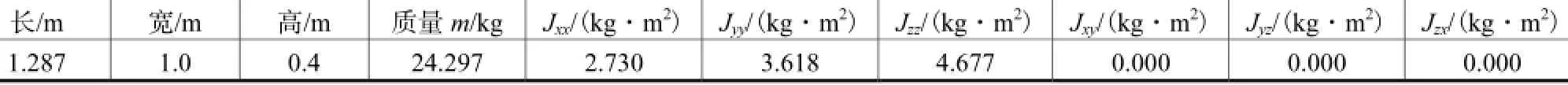
表2 导管架模型物理参数Tab.2 Physical parameters of jacket model

表3 拖航试验参数Tab.3 Parameters for towing experiment

2.3.2 拖缆力结果验证

3个组次试验缆绳力实测结果与数学模型计算结果对比如图9所示，二者基本符合．组次1的波高较大，拖航速度较小，拖缆力峰值及随时间变化的数值模拟结果与实测结果符合较好．组次2与组次3的波高大小相同，组次3的拖航速度较大．由结果对比可见，组次2相位和幅值的符合程度更好，而组次3的相位约有5%的差异，原因可能是拖航速度较大及实测误差引起．此外，由于数学模型中未考虑杆件对水流和波浪的反馈影响，也有可能造成计算有一定偏差．

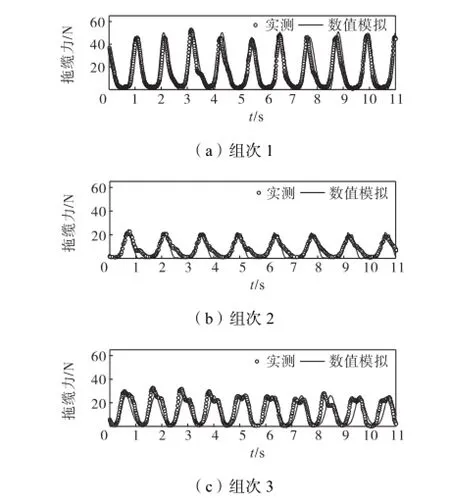
图9 拖缆力模型试验和数值模拟结果对比Fig.9 Comparison between numerical results and measurements of line tension

2.4 波浪入射角对拖缆力及导管架位移响应的影响

针对不同波浪入射角度，对导管架响应和拖缆力进行数值模拟．入射角度从顺浪(入射角为0°)到逆浪(入射角180°)之间分为6等份，每30°做一次模拟(见图10)．波浪要素如表4所示．

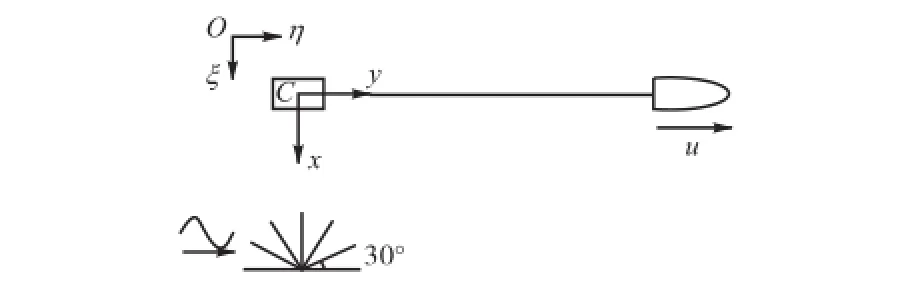
图10 不同波浪入射角拖航示意Fig.10 Sketch of various waves incident angle in towing

表4 试验波浪要素Tab.4 Wave conditions for simulation

1) 拖缆力

图11和图12分别为不同波浪入射方向拖缆力数学模型计算结果．可以看出，逆向30°浪时拖缆力最大，大于正逆向时的拖缆力；横向浪时拖缆力较小．

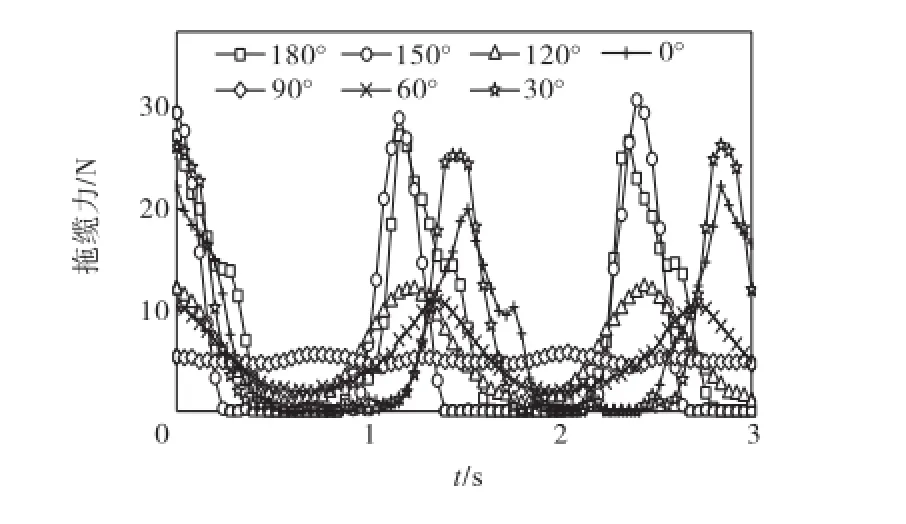
图11 不同波浪入射角拖缆力数学模型计算结果Fig.11 Numerical results of line tension with time for different waves incident angle

图12 拖缆力峰值随波浪入射角变化数学模型计算结果Fig.12 Numerical results of variation of peak value of line tension with waves incident angle

2) 垂向位移和纵摇响应

图13给出了垂向位移幅值随波浪入射角变化的计算结果，表明随着入射角的增加，位移量呈现先减小后增大的趋势．在横浪条件下导管架垂向位移最小．图14为逆浪和横浪作用下导管架纵摇角的变化，显然，横浪引起的导管架纵摇远小于逆浪．而逆浪时，受拖缆限制，导管架的向后纵摇位移较小，向前纵摇与波浪的振荡过程也并非完全吻合，而是有一个向后的回摇过程，这与缆绳对导管架的制约作用有关．最大纵摇幅度约为6°．

图13 垂向位移数学模型计算结果Fig.13 Numerical results of vertical displacement amplitude

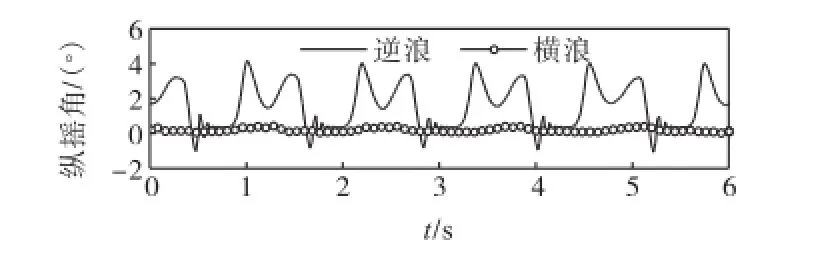
图14 纵摇角模型计算结果Fig.14 Numerical results of pitching angle

3) 横向位移

导管架在拖航过程中若产生横向位移，则缆绳与拖船行进方向不再平行．图15为横向规则波作用下导管架的横向位移计算结果．导管架位移过程形状为谐波，并未产生漂移，原因可能是没有考虑波浪的非线性特征．

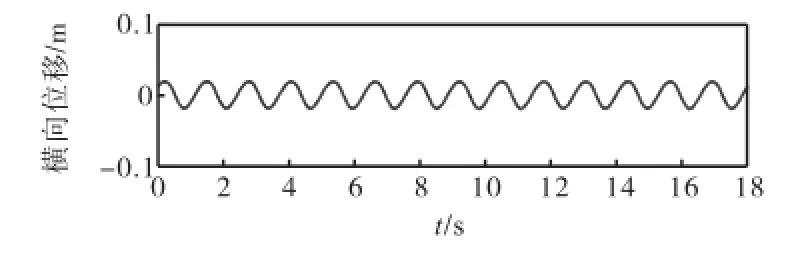
图15 横浪作用下导管架横向位移计算结果Fig.15 Numerical results of lateral displacement of jacket under waves in traverse direction

2.5 水流流向对拖缆力和导管架位移的影响

水流对导管架的作用与波浪不同．当水流方向与拖船航行方向成一定角度时，由于水流持续作用于导管架，使得拖缆与航向成一固定夹角(图16)．按照拖船航行方向与水流方向夹角不同，设定6个方向(表5)计算拖航力和导管架位移．流速为0.2,m/s，拖航速度为0.188,m/s．水流与拖航方向成不同角度下，各组平衡位置以及拖缆力计算结果如表5所示．由表5可以看出，水流方向与拖航方向相反时，拖缆力最大．

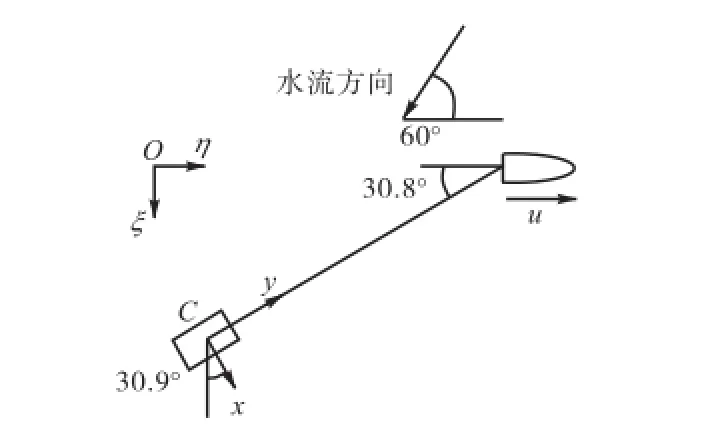
图16 水流方向与拖航方向成60°夹角时的拖航示意Fig.16 Sketch of relative position of tugboat and jacket for 60°inverse-incident current

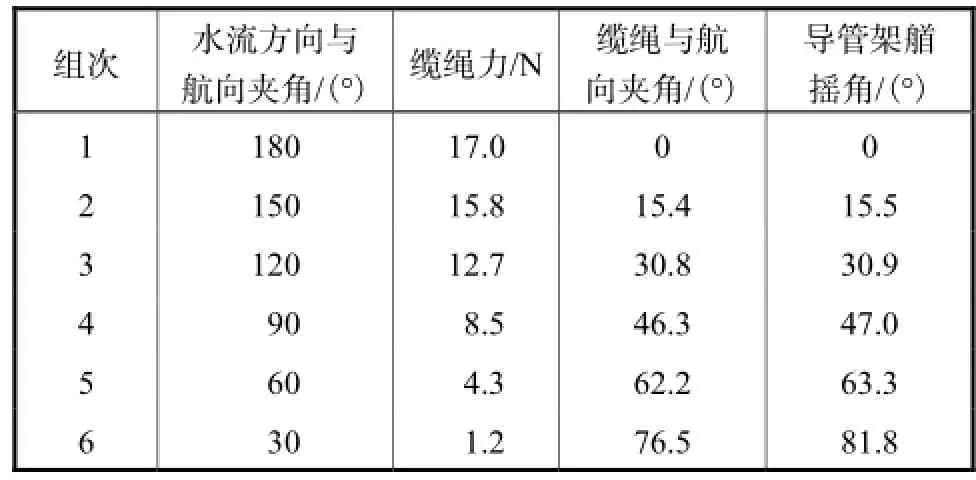
表5 水流作用下拖航平衡状态的计算结果Tab.5 Numerical results of line tension in different incident direction of current for towing in equilibrium angle

图17显示了缆绳与航向夹角(平衡角)随横向流速Uξ与导管架在纵向相对速度Uη-UJ比值的变化．从图中可知，比值越大，缆绳与航向所成角度越大．当比值为1时，夹角为45°．该结果表明，导管架在单根缆绳条件下拖航时，要注意横流的影响．

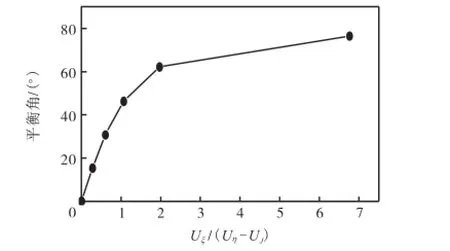
图17 缆绳与航向夹角随横纵向相对流速比的变化Fig.17 Variation of angle between line and navigation direction with ratio of flow in traverse direction to that in longitudinal direction

3 结 语

本文提出了一种导管架浮运稳定性计算模型．采用线性波理论和莫里森方程计算流体动力，并采用4阶龙格-库塔方法求解方程，对模型模拟导管架在静水条件下的振荡特性进行了测试，得到了波浪作用下的共振效应；同时，还将物理模型实测的3组拖缆力结果与数值模拟结果进行了对比，二者符合较好．最后对不同波浪入射角度和水流流向条件下导管架拖航情况进行了数值模拟，结果表明，逆向30°浪时拖缆力最大，大于正逆向浪的情况．分析了缆绳与拖航方向的平衡角随横纵向流速比的变化，得出比值越大，拖缆与航向的平衡角越大的结论．

［1］ 张志明，胡家顺. 我国大型开敞式码头结构设计与施工技术现状及发展趋势探讨[C]// 港口工程分会技术交流文集. 北京：人民交通出版社，2005：91-100.

Zhang Zhiming，Hu Jiashun. Present situation and development tendency on the design and construction technology of large open style offshore wharf in china[C]// Proceedings of Technical Communication of Port Engineering Branch. Beijing：China Communications Press，2005：91-100(in Chinese).

［2］ 程泽坤，程培军. 外海开敞水域码头结构新型式[J].水运工程，2008(10)：35-40.

Cheng Zekun，Cheng Peijun. New type jetty structure in offshore open waters[J]. Port and Waterway Engineering，2008(10)：35-40(in Chinese).

［3］ Jo C H，Kim K S，Kim Jae H，et al. Criterion of offshore jacket launching analysis[C]// Proceedings of the 11th (2001)International Offshore and Polar Engineering Conference. Stavanger，Norway，2001：90-96.

［4］ Jo C H，Kim K S，Lee S H. Parametric study on offshore jacket launching[J]. Ocean Engineering，2002，29(15)：1959-1979.

［5］ Zhang Guangfa，Ji Zhuoshang，Li Tieli，et al. Calculation of wave and current loads on launching offshore jacket[J]. Journal of Marine Science and Application，2006，5(4)：1-7.

［6］ 杨晓刚. 文昌油田导管架扶正分析[J]. 中国海上油气：工程，2003，15(1)：18-38.

Yang Xiaogang. Self-upend analysis of the jacket in Wenchang oil field[J]. China Offshore Oil and Gas：Engineering，2003，15(1)：18-38(in Chinese).

［7］ He Min，Li Huailiang，Wu Zhiquan，et al. Jacket launch and self-upending analyses with small-hole flooding scheme[C]//Proceedings of the 20th(2010) International Offshore and Polar Engineering Conference. Beijing，China，2010：400-407.

［8］ Pinheiro Jacob Breno，de Almeida Bahiens Rodrigo，Fabrício Nogueira Correa，et al. Parallel implementations of coupled formulations for the analysis of floating production systems(Part I)：Coupling formulations[J]. Ocean Engineering，2012，55：201-208.

［9］ 张光发，纪卓尚，李铁骊，等. 导管架下水过程中浮力及浮心精确计算[J]. 海洋工程，2007，25(1)：15-20.

Zhang Guangfa，Ji Zhuoshang，Li Tieli，et al. Precise calculation of buoyancy and its center for launching Jackets[J]. The Ocean Engineering，2007，25(1)：15-20(in Chinese).

［10］ Mutlu Sumer B，Jørgen Fredsøe . Hydrodynamics Around Cylindrical Structures[M]. Singapore：World Scientific，1997.

Numerical Model and Its Validation for Floating Simulation of Jacket-Type Wharf Under Waves and Currents

Li Shaowu1，Xia Lujun1，Zhang Wenzhong2
(1. State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China；2. Tianjin Port Engineering Institute Limited of China Communications Construction Company，Tianjin 300222，China)

A mathematical model is proposed for the simulation of floating jacket. In the model, the jacket is considered as a rigid body, and waves, currents and the towing line are the main loads. The governing equations are established for the movement of the jacket based on the rigid body dynamics, in which the wave and current loads are estimated by Morison theory. The governing equations are solved by the 4th order Runge-Kutta method. The displacements in 6 degrees of freedom and the tension of the mooring rope are simulated. The calculated tension of the line is compared with the result measured in a wave flume, which shows good agreement. The results of displacement in the towing process under waves and currents are analyzed according to the results of numerical calculation, and it is found that the tension of the line reaches its largest value if wave incident angle is around inverse 30°, which is greater than that in the case of normally inverse-incident wave. The variation of the balance angle between towing direction and towing line with the ratio of the current velocity in the traverse direction to that in the longitudinal direction is analyzed, and it is found that the bigger the ratio, the bigger the angle is.

jacket-type wharf；Morison equation；floating method；stability

P752

A

0493-2137(2013)05-0401-07

DOI 10.11784/tdxb20130504

2012-12-11；

2012-12-25.

国家自然科学基金创新研究群体基金资助项目(51021004)．

李绍武（1962— ），男，博士，教授.

李绍武，lishaowu@tju.edu.cn.