航空拖曳诱饵系统机动过程缆绳张力仿真
2021-10-20杜一江
杜一江
海军航空大学 航空基础学院,烟台 264000
随着导弹先进制导技术的发展,飞机在空中的生命力安全受到严重的威胁,机载自卫电子干扰和机动躲避已无法满足飞机安全需要[1]。为保护飞机的安全,拖曳式诱饵应运而生[2]。
拖曳式诱饵通过辐射强大的电磁信号,模拟飞机的运动特性,从而达到干扰敌方来袭导弹雷达、保护己方飞机的目的[3]。诱饵在空中主要依靠缆绳由载机拖曳飞行,载机、缆绳、诱饵构成了复杂的空中多体系统,对其进行动力学建模,分析其动力学特性,尤其是对缆绳张力的动力学分析与计算,对航空拖曳诱饵系统的研制与开发,具有重要的工程意义。
目前公开发表的论文中,对拖曳式诱饵系统的缆绳张力研究较少,但对其他航空拖曳系统缆绳的动力学特性进行了一定的研究。
Kolodne[4]和Wu[5]研究了无气动力条件下拖曳缆绳的非线性运动,并且提出了获得渐近解的方法;Triantafyllou[6-8]等采用连续体模型对拖缆动力学问题进行建模,并且对缆绳模型进行了改进,使得系统动力学方程的数值求解变得比较稳定。Kamman和Huston[9]等基于有限元方法,提出了一种缆长可变的拖曳系统动力学建模方法。Liu等[10]基于凯恩方程,为拖曳系统建立了一个多体动力学模型,对航空拖缆释放过程中的动态特性进行了研究。
Narkis[11]主要研究了航空拖曳系统运动过程中的拖缆应力的变化情况,其结果表明拖缆在紧绷的状态下急剧减速将使张力出现极值,研究中还提出了一种渐进解的分析方法,用于求解水平面内拖缆的最大峰值应力。Matuk[12]研究了载机在180度转弯时的拖曳系统机动过程。由于缆绳的“鞭状”效应,载机完成转弯后出现最大张力。对缆绳末端的张力进行了十二次飞行测试,发现测得的力均小于理论预测值。Sun等[13]用飞行数据对集中质量模型描述的可伸长缆绳的航空拖曳系统进行了模型验证,并利用模型预测控制对张力约束的拖曳系统进行最优控制。Doroudgar[14]对绳系无人机系统的缆绳进行了动力学建模和仿真,研究了无人机盘旋模式下,缆绳最大张力出现时缆绳的空间构型等问题。
王一飞[15]对航空拖靶系统在匀速直线运动飞行时的动力学方程进行了求解,得到了无扰动情况下拖曳系统的稳定解,并用实验验证了所求拖曳缆绳张力的正确性。田新峰等[16-17]对平衡态下的多阶组合航空拖缆进行了仿真研究,给出了平衡态下张力沿缆绳的分布情况。马东立等[18-19]应用集中质量模型,建立了基于旋量的动力学方程,提出了缆绳与拖曳式飞行器的耦合条件,使模型更加精确,开发了张力再现算法,提高了系统的计算效率。
本文在前人集中质量模型的基础上,进一步考虑缆绳内部的阻尼力,建立了缆绳的质量弹簧阻尼模型。该模型和诱饵弹的六自由度动力学模型一起构成完整的拖曳诱饵系统动力学模型。在此基础上,本文对拖曳诱饵系统的直线加速和机动转弯过程进行了飞行仿真,重点分析这2种典型机动过程中缆绳张力在缆绳内部的传递规律及其影响因素,据此给出结论。
1 动力学建模
1.1 缆绳动力学模型
本文采用质量弹簧阻尼模型,将缆绳离散为一定数量(n)的缆绳微元,微元段的质量集中在微元段的端点处,即2个微元段的连接点处。考虑到缆绳可伸长变形的特性,将微元段简化为只能承受张力不能承受压力的弹簧。同时考虑缆绳内部的阻尼作用,进一步假设该弹簧具有一定的阻尼。这样就将缆绳离散为一系列由阻尼弹簧连接的质量节点,微元段的重力、气动力及微元段之间的相互作用力均作用在该质量节点上。缆绳的质量弹簧阻尼模型如图1所示。对每一个质量节点进行受力分析,根据牛顿第二定律就可以建立缆绳的动力学模型[20]。

图1 质量弹簧阻尼模型Fig.1 Mass spring dumping model
以地面某一点为坐标原点,建立惯性坐标系O-XYZ,第j个节点的坐标为
rj=[xj,yj,zj]
(1)
对式(1)求微分得到节点的速度为
(2)
对式(2)求微分得到节点的加速度为
(3)
节点受到重力、气动力、弹性力和阻尼力,其动力学方程可以写为
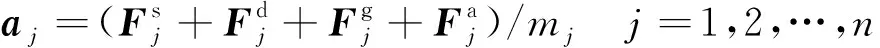
(4)

1.1.1 弹性力
缆绳节点j受到的弹性力来源于相邻的2个弹簧微元,根据胡克定律,缆绳节点j受到的弹性力与缆绳的形变成正比,设第j段弹簧微元作用于节点j的弹性力大小为Tj,则
(5)
式中:
(6)
E为缆绳的弹性模量;A为缆绳的横截面积;Lsj为第j段缆绳微元未拉伸时的长度;rf为载机与缆绳连接点处的位置矢量。由于缆绳只能承受张力,不能承受压力,故当缆绳微元伸长量小于零时,微元张力为零。缆绳节点的弹性力矢量为
(7)
1.1.2 阻尼力
缆绳微元阻尼力与微元应变率相关,其计算公式为
(8)
式中:
(9)

1.1.3 重力
缆绳节点j受到的重力可以表示为
(10)
1.1.4 气动力
查阅资料发现,在缆绳微元段的气动力建模方面,由Hoerner[21]于20世纪60年代提出的模型应用最为广泛,该模型要求缆绳微元段的横截面为圆形,并且要求流场为低雷诺数流场。本文中的缆绳微元段及流场均符合该模型的使用条件。
根据Hoerner[21]的气动力模型,第j段微元的升力系数CLj和阻力系数CDj可由式(11)求得
(11)
式中:θj为第j段微元的攻角,由式(12)求得
(12)
其中:Cfj、Cnj分别为切向力和法向力系数,由式(13)、式(14)求得
Cfj=
(13)
(14)
其中:Mpj、Mnj分别为第j段微元的切向和法向马赫数。
缆绳微元j的升力和阻力矢量可以写为
(15)
式中:d为缆绳的直径;ρj为第j段缆绳微元所处高度的大气密度,第j段缆绳微元的气动力为
(16)
1.2 诱饵弹动力学模型
拖曳式诱饵的位置、速度以及姿态响应对缆绳张力的变化有着直接的影响,缆绳张力的变化也必将对诱饵的姿态产生影响,它们之间相互耦合。故进行缆绳张力的动力学仿真必须建立六自由度的诱饵弹动力学模型。
1.2.1 坐标系及其转换关系
本文中建立了诱饵弹的弹体坐标系Od-XdYdZd及气流坐标系Oa-XaYaZa,如图2所示。其中,弹体坐标系Od-XdYdZd原点位于诱饵弹的质心,OdXd轴方向平行于弹体纵轴指向前,OdYd轴垂直于OdXd轴向上,OdZd轴垂直于弹体纵平面指向右。气流坐标系Oa-XaYaZa的原点也位于质心,OaXa轴方向指向气流来流方向,OaYa轴垂直于OaXa轴向上,OaZa轴垂直于OaXaYa平面指向右。

图2 弹体坐标系和气流坐标系Fig.2 Decoy body axes and wind axes
弹体坐标系Od-XdYdZd和气流坐标系Oa-XaYaZa之间的转换欧拉角有迎角α和侧滑角β,从气流坐标系到弹体坐标系的转换矩阵为
(17)
弹体坐标系和惯性坐标系之间的转换欧拉角有滚转角φ、俯仰角θ、偏航角ψ,从惯性坐标系到弹体坐标系的转换矩阵为
Tdg=Tx(φ)Tz(θ)Ty(-ψ)
(18)
(19)
(20)
(21)
1.2.2 动力学方程
其动力学方程可以写为
(22)

(23)
式中:u、v、w为弹体坐标系下的3个速度分量;p、q、r为诱饵弹绕弹体坐标系三轴的转动角速度。气动力在弹体坐标系表示为
(24)
式中:D、L、C分别为阻力、升力、侧力。重力在弹体坐标系表示为
(25)
缆绳牵引力在弹体坐标系表示为
(26)
将式(23)~式(26)代入式(22),由此得到诱饵弹的平动动力学方程为
(27)
诱饵弹的转动动力学方程为
(28)
式中:Ix、Iy、Iz、Izx为诱饵弹的转动惯量和惯性积;Mx、My、Mz为诱饵弹所受合外力矩在弹体坐标系的3个分量。式(27)和式(28)共同构成了诱饵弹的六自由度动力学方程。
2 仿真分析
航空拖曳诱饵系统机动过程仿真通常包括直线加减速、机动转弯、俯冲与跃升等飞行状态下的仿真。本文对直线加速和机动转弯2种典型机动动作进行仿真研究,计算缆绳张力在这些过程中沿缆绳的分布变化情况。
本文的仿真采用的拖缆参数来源于文献[22],如表1中所示。

表1 缆绳参数表[22]Table 1 Parameters of cable[22]
本文中仿真采用的拖曳诱饵弹模型参数如表2 和表3所示表中:CLα为升力线斜率;CCβ为侧向力系数对侧滑角的导数;Cmzα为俯仰力矩系数对迎角的导数;Cmyβ为偏航力矩系数对侧滑角的导数;Cmxp为滚转力矩系数对滚转角速度的导数;Cmyq为偏航力矩系数对偏航角速度的导数;Cmzr为俯仰力矩系数对俯仰角速度的导数;CD0为零升阻力系数。

表2 诱饵的质量和几何模型[19]Table 2 Weight and geometry parameters of decoy[19]

表3 诱饵气动特性导数[19]Table 3 Aerodynamic characteristics parameters of decoy[19]
2.1 直线加速
假设拖曳式诱饵系统初始以100 m·s-1的速度作匀速直线运动,然后以30 m·s-2的加速度匀加速至400 m·s-1。拖曳诱饵系统的轨迹图如图3所示,在载机加速过程中,拖曳式诱饵跟着加速,并在垂直平面内波动上升,逐渐趋于平稳。

图3 直线加速运动轨迹图Fig.3 Trajectory of linear accelerated motion
选取载机与缆绳连接处的缆绳微元进行张力对比分析,得到的结果如图4所示。图中,实线为拖曳系统由匀速直线运动过渡到匀加速直线运动过程中缆绳微元的张力变化情况;点划线表示拖曳系统匀加速直线运动时(准平衡状态下)缆绳微元的张力变化情况;点线表示拖曳系统在同样速度下匀速直线运动时(平衡状态下)缆绳微元的张力变化情况。从图中可以得出:① 随着系统速度的增大,缆绳的张力逐渐增大,这是由于诱饵弹和缆绳的气动阻力随着速度增大而增大的缘故;② 加 速状态下缆绳的张力不仅需要平衡诱饵弹和缆绳的气动力、重力,还需要平衡它们的惯性力,故匀加速直线运动准平衡状态下的缆绳张力会比同样速度匀速直线运动的缆绳张力多出一个固定值;③ 系统由匀速直线运动转变为匀加速直线运动过程中,缆绳张力在匀加速直线准平衡态张力值附近波动,并最终趋于准平衡态。这种波动本质上是由于缆绳弹性的存在导致缆绳中前后微元段的张力传递存在时滞性的缘故。前一个微元段的张力不能立刻传递给后一个微元段,而是通过前后微元节点位置变化进行传递。当前后微元段有张力差时,前后微元节点的加速度存在差值,加速度差导致速度差,速度差导致位置差,位置差引起后微元段的形变量变化,进而引起张力的变化。在这个过程中,位置变化滞后于速度变化,速度变化滞后于加速度变化。这种滞后性导致缆绳中的张力在准平衡态附近波动,并在缆绳微元的阻尼作用下,趋于平衡。

图4 匀加速直线运动时缆绳张力随载机速度变化情况Fig.4 Cable tension vs aircraft velocity during uniform linear accelerated motion
本仿真从牵引点(载机与缆绳连接点)到拖曳点(缆绳与诱饵连接点)依次选取了10个缆绳微元作为采样点,来观察缆绳中张力波动的情况,结果如图5所示,图中S为从载机与缆绳连接点处起算的缆绳绳长。从图中可以看出,机动过程中同一时刻缆绳的最大张力值在牵引点处产生,从牵引点到拖曳点张力沿缆绳逐渐减小;后一个采样点的张力波动情况总是跟随并滞后于前一个采样点;各缆绳微元在阻尼作用下趋于平衡。
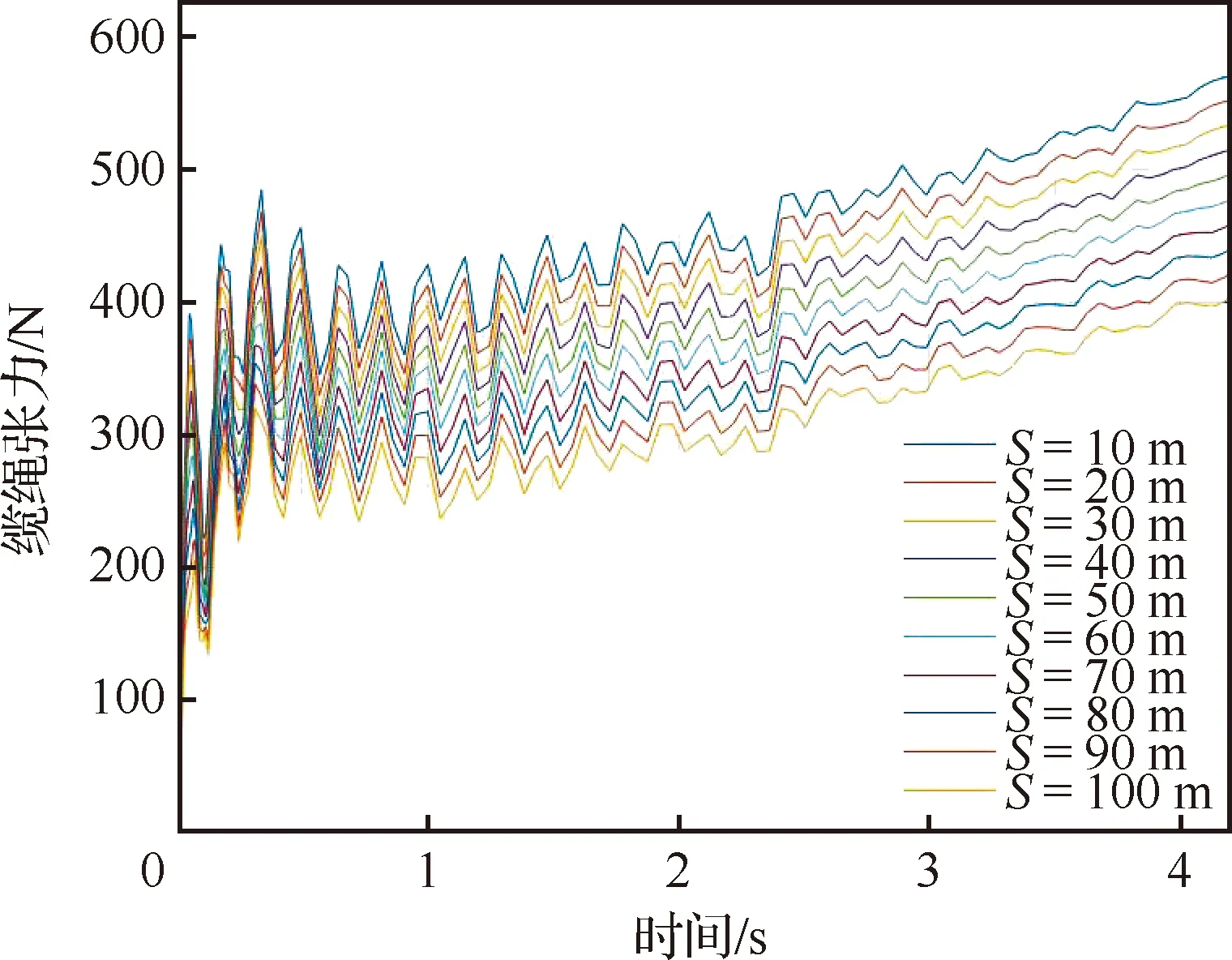
图5 匀加速直线运动缆绳不同点处张力随时间变化情况Fig.5 Tension at different point of the cable vs time during uniform linear accelerated motion
影响缆绳张力波动幅值和传递速度的主要因素有载机加速度、载机飞行高度、缆绳弹性模量和缆绳直径等,本文采用分离变量法,对以上4个因素进行了参数化仿真。
2.1.1 载机加速度
载机初始速度为100 m·s-1,飞行高度9 km,加速度分别取为10 m·s-2、20 m·s-2、30 m·s-2;缆绳弹性模量为100 GPa,直径为3 mm。仿真得到缆绳张力波动情况如图6所示。从图中可得:加速度越大,张力波动越剧烈,达到稳态的时间越长。这是由于加速度越大,缆绳微元段需要承受的惯性力越大,微元段形变量越大,张力传递的时滞性越显著。因此,在工程实际使用过程中,要根据缆绳的强度对飞行速度和加速度加以限制。

图6 不同加速度下缆绳张力波动情况Fig.6 Fluctuation of cable tension with different acceleration
2.1.2 载机飞行高度
载机初始速度为100 m·s-1,加速度30 m·s-2,飞行高度分别取为3 km、6 km、9 km;缆绳弹性模量为100 GPa,直径为3 mm。仿真得到缆绳张力波动情况如图7所示。从图中可得:高度越低,缆绳稳态张力越大。并且飞行速度越大,这种变化越显著。这是由于飞行高度越低,空气密度越大,气动阻力越大,需要的缆绳张力就越大的缘故。
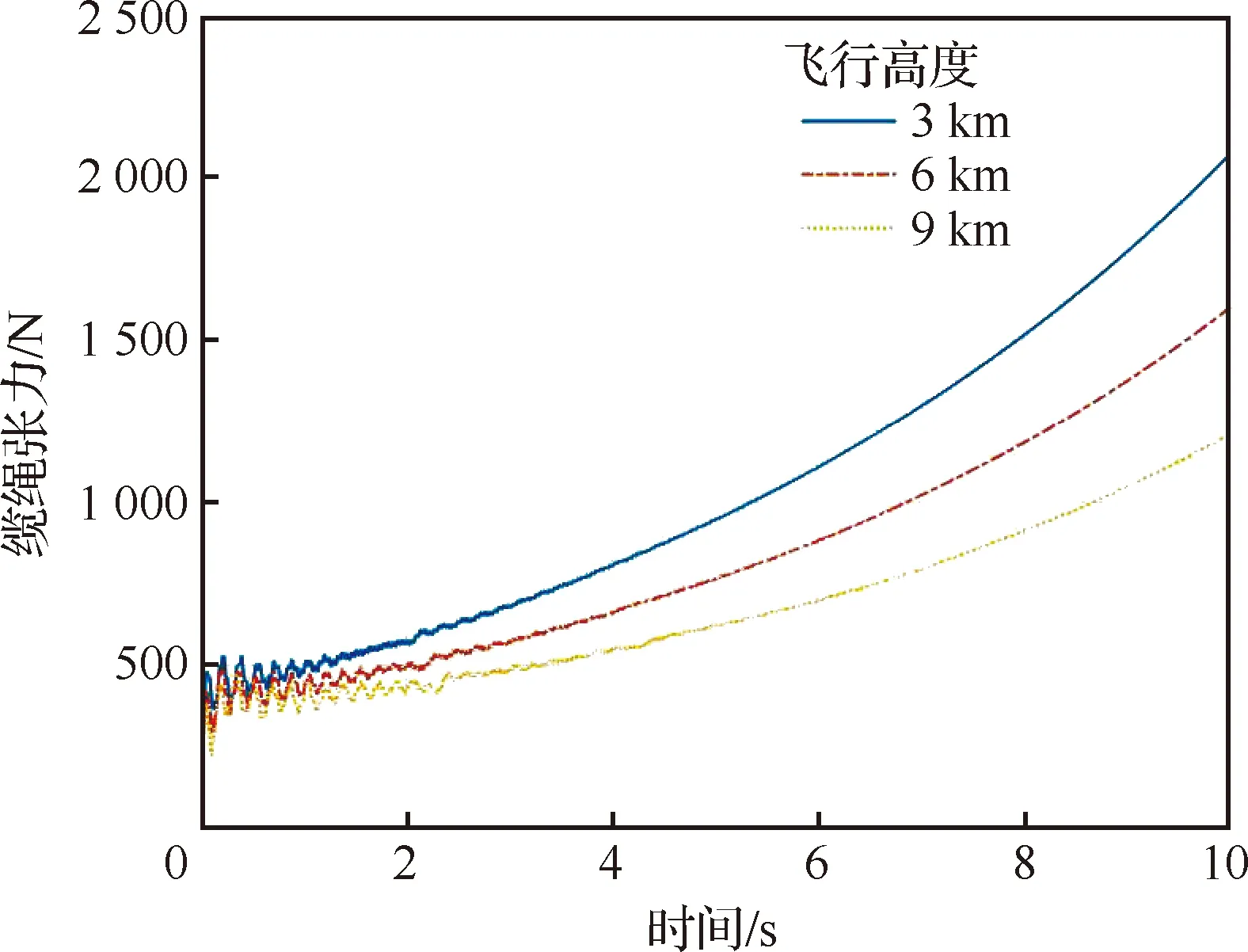
图7 不同飞行高度下缆绳张力波动情况Fig.7 Fluctuation of cable tension with different flight altitudes
2.1.3 缆绳弹性模量
载机初始速度为100 m·s-1,加速度为30 m·s-2,飞行高度为9 km;缆绳直径为3 mm,缆绳弹性模量分别取1 GPa、10 GPa、100 GPa。仿真结果如图8所示。从图中可以看出,弹性模量越小,张力偏离准平衡位置的偏离量越大,达到稳态的时间越长。这是由于弹性模量越小,相同的张力作用下,缆绳微元的形变量越小,张力传递的时滞性越显著的缘故。因此,较大的弹性模量,可以提高张力在缆绳中的传递速度,减小张力的波动幅值。

图8 不同弹性模量下缆绳张力波动情况Fig.8 Fluctuation of cable tension with different elastic modulus
2.1.4 缆绳直径
载机初始速度为200 m·s-1,加速度为30 m·s-2,飞行高度为9 km;缆绳直径分别取3 mm、5 mm、7 mm,缆绳弹性模量为100 GPa。仿真得到缆绳张力波动情况如图9所示。从图中可得:缆绳直径的增加将显著增加缆绳的稳态张力和波动幅值。这是由于缆绳直径越大,缆绳的横截面积和质量越大,相同速度下,缆绳受到的气动阻力、重力、惯性力就越大,缆绳内部的张力也相应增大。因此,减小缆绳直径有利于减小缆绳内部张力,但过小的缆绳直径将导致缆绳强度不足,工程上需要在二者之间寻求平衡。
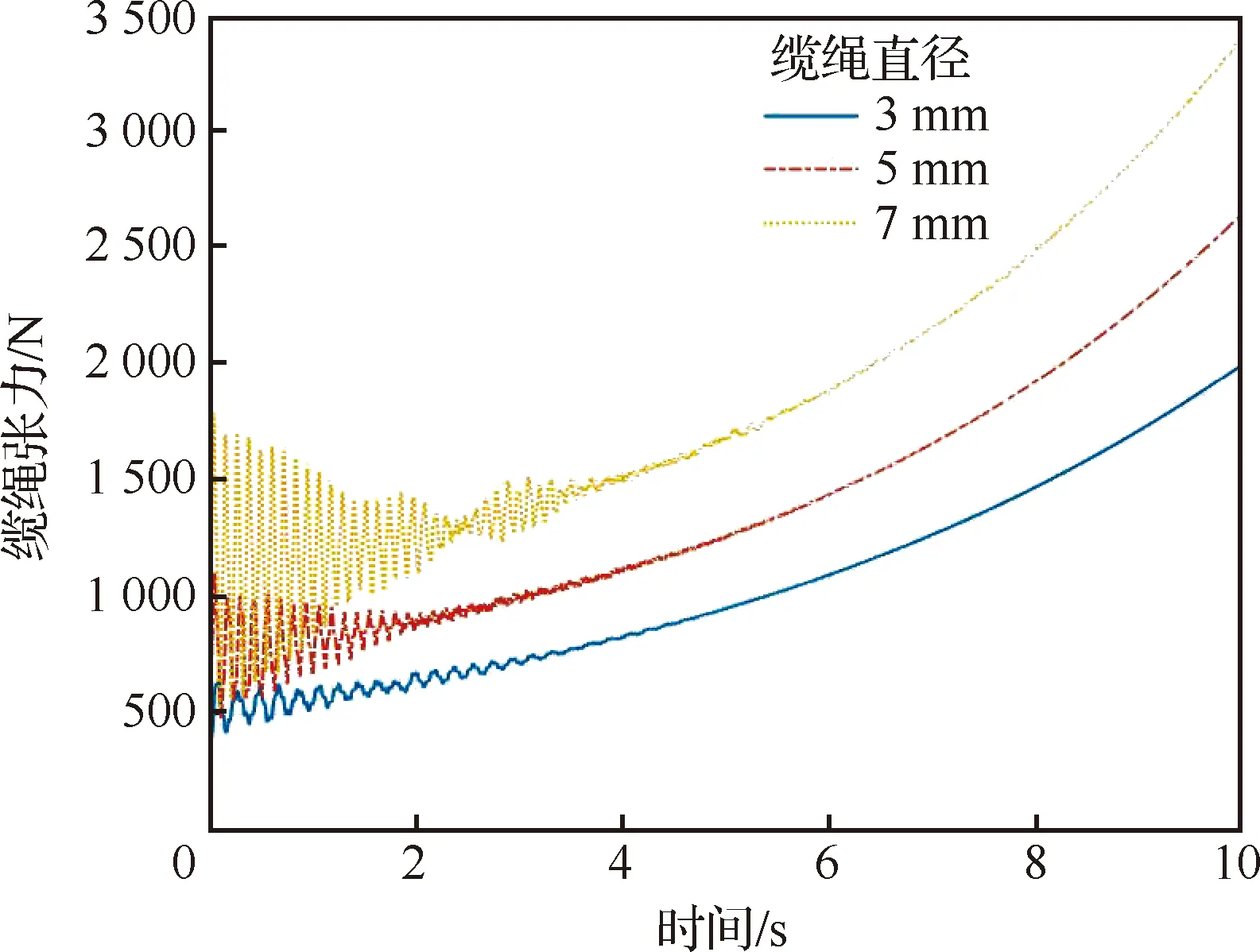
图9 不同缆绳直径下缆绳张力波动情况Fig.9 Fluctuation of cable tension with different cable diameters
2.2 机动转弯
为研究拖曳式诱饵系统机动转弯过程中的缆绳张力变化情况,本文设置如下飞行场景:系统刚开始处于匀速直线运动状态,然后从某一时刻开始,载机以某一固定角速度开始在水平面内转弯,此时,缆绳和诱饵也将随着载机一起做转弯运动。图10显示了系统的运动轨迹,从图10中可以看出,在转弯过程中,诱饵弹会被“甩”离转弯中心,并在垂直平面内有较大幅度的沉浮运动。
图11展示了转弯过程中缆绳上各点处的张力变化情况,转弯过程中载机速度保持为200 m·s-1,转弯角速度为0.2 rad·s-1,从图中可以看出:刚开始转弯时,缆绳张力缓慢增加,大约1 s后,突然承受一个较大的峰值张力,后张力不断震荡,最后在阻尼作用下趋于稳态。这是由于诱饵弹转弯初始,转弯侧向加速度由载机与缆绳连接点向牵引点传递,用于平衡缆绳微元段侧向惯性力的附加张力缓慢增加,当侧向加速度传递至诱饵弹,附加张力还需要平衡诱饵弹的侧向惯性力,由于诱饵弹的质量远大于缆绳微元段,因此此时缆绳的附加张力会急剧增加,出现一个较大的峰值张力。从图中还可以看出,转弯过程中的稳态张力值高于初始的稳态张力值,这是由于缆绳张力还需要平衡缆绳及诱饵弹向心加速度产生的附加惯性力的缘故。

图11 机动转弯过程缆绳张力变化图Fig.11 Cable tension vs time during turning maneuver
在机动转弯的仿真中,载机飞行高度、缆绳弹性模量、缆绳直径对缆绳张力的影响与直线加速仿真相类似,在此不再赘述。本文重点分析转弯过程中的转弯角速度对缆绳张力的影响。
转弯过程中载机飞行高度为9 km,速度大小保持为200 m·s-1, 转弯角速度分别取为0.1 rad·s-1、0.2 rad·s-1、0.3 rad·s-1,缆绳弹性模量取100 GPa,缆绳直径为3 mm。仿真结果如图12所示。从图中可以看出,转弯角速度越大,缆绳达到稳态时的张力越大,张力波动越剧烈,达到稳态的时间越长。这是由于相同载机速度下,载机角速度越大,系统的向心加速度越大,缆绳微元段及诱饵弹的侧向惯性力就越大,缆绳上的附加张力就越大的缘故。

图12 转弯角速度对缆绳张力的影响Fig.12 Effect of turning angle velocity on cable tension
3 结 论
1) 航空拖曳诱饵系统机动过程中,缆绳上某一点处的张力等于那一点以下缆绳所受合外力、惯性力以及诱饵弹所受合外力、惯性力的矢量和。
2) 航空拖曳诱饵系统机动过程中,张力在缆绳中的传递存在时滞性,这导致缆绳中张力会产生波动。
3) 张力波动幅值及稳态时间与载机加速度、缆绳弹性模量、缆绳直径有关。载机的加速度越大,缆绳弹性模量越小,缆绳直径越大,张力波动越剧烈,达到稳态时间越长。
4) 载机由匀速直线运动转入盘旋运动时,缆绳会承受一个较大的峰值应力,转弯角速度越大,该峰值应力越大。
