基于A*算法的永磁球形电动机闭环控制方法研究

雍爱霞

(合肥电子工程学院，安徽合肥230037)

0 引 言

目前国内的永磁球形步进电动机的研究参照的是美国Hopkins大学Gregory S.Chirikjian等人设计的原型结构［1－3］，已有大量的文献对该类型的电机进行了基础研究的探讨［4－5］。转子球体在三维空间的转角检测是电机控制中迄待解决的关键技术，同时也是制约电机理论研究和工程应用的瓶颈，迄今为止针对方位角检测系统的设计和探索主要有滑轨式、喷涂式、摄像头式等，其中非接触式方位角检测的设计是主要的研究方向，同时将检测的设计应用到电机控制中去是最终的目的。本文尝试着研究球形步进电动机的闭环控制转动，建立加权有向图模型，针对无串扰的确定任务的转动和有串扰的重新定位等。

1 线圈换相的理论分析和仿真

永磁球形步进电动机是一种新型的多自由度电机，其结构和运动机理都与传统电机完全不同，转子内部嵌有80个永磁体按照某种特定规则排列分布，其坐标位置的计算见文献［1］的参数设计。永磁体的N极指向球外，定子内腔半球形，非导磁材料支撑，内部放置16个带铁心的线圈，定子被固定在一个支座上，每个定子线圈都可以分别通电的。通过某种特定的导电策略给线圈通电，从而可以拖动转子按期望轨迹进行转动。每个铁心线圈周围有一个光电编码环，其中嵌入的六个光电编码器距离相等，因此随着转子球体的空间运动，在不考虑光电编码器的分辨率情况下，96个光电编码器的输出与空间方位角一一对应，文献［6－7］探讨了转子球体喷涂式方位角检测的方法。

转子球体做的三维运动保持球心不变，电机的通电线圈和永磁体的吸附将产生在空间中的某步距转动，然后达到一个空间的某个稳定角度，对于该种结构的球形电机而言，要达到稳定状态至少需要两个永磁体和两个相应的通电线圈吸附在一起。理论上来说通电的线圈个数越多，电机转动就越精细、转动路径就越多，能够到达空间的方位角也就越多，但球形电机的距角特性、转动分析和动力学空间平衡将变得更为复杂，为了控制和计算简便，这里只研究每次两个线圈同时通电情况下转子球体的转动分析。令球形电机初始状态下定子线圈与永磁体的分布如图1所示，文献［4］详细地论述了三维电磁场，可知每个永磁体所在位置处磁场最强，永磁体之间的磁场则较弱，当给定子上的两个线圈同时通电后，与定子通电线圈距离相等并分别位于这两个线圈最近的永磁体对将受力吸附在一起，不同的通电线圈对使得电机产生不同的旋转要素。

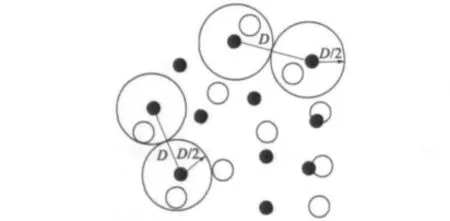
图1 部分线圈/永磁体的初发始位置

其中 Mi的坐标为(xi，yi，zi)、Mj的坐标为(xj，yj，zj)、Wm的坐标为(xm，ym，zm)、Wn的坐标为(xn，yn，zn)，D为永磁体 Mi和永磁体 Mj之间的距离。令永磁体对(Mi，Mj)和线圈对(Wm，Wn)的距离相等，分别计算这组永磁体对和通电线圈对之间的距离，令:

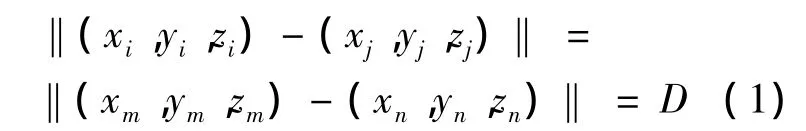
将文献［8］中符合通电条件的线圈对和永磁体对的坐标公式修改为下式，就认为可以给这两个线圈通电，转子将产生相应的转动。

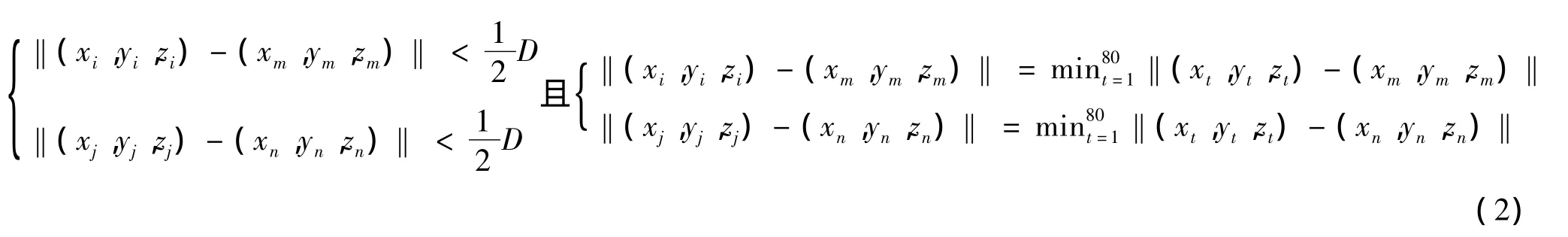
2 球形步进电动机闭环控制方法

作为一种复杂的三维空间旋转机构，根据符合换相条件的每一对通电线圈对/永磁体对产生一次三维转动步距角的特点，将所有转动路径的集合用加权有向图模型来描述，如此以来复杂的运动控制问题就可以描述成有向图的遍历。

闭环控制系统的加权有向图记为D=(A，R)，如图2所示，其中A、R分别表示D的顶点集合和弧集合，弧记为(Ai，Aj)，表示这两个顶点间有一次步距运动，加权有向图模型的闭环控制算法需要计算的参量包括当前位置下方位角、步距角旋转的四元数组、符合通电条件的永磁体对/线圈对。其中旋转四元数组来表示有向图的权值，因此若干次步距角的组合旋转可以充分利用四元数组的计算优势，方便提取转轴和转角等旋转要素，且便于编程。

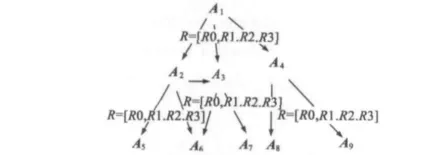
图2 闭环控制的加权有向图

有向图中的顶点为从初始方位角转动到当前位置下的群元矩阵A，在三维实坐标空间R3中将保持球心不变的转动变换构成三维转动群［9］，选取特殊实正交矩阵SO(3)中矩阵余弦A作为加权有向图的顶点，可以直观地在三维空间中进行方位角标定，且方便地与四元数组进行互换［10］，其构成:

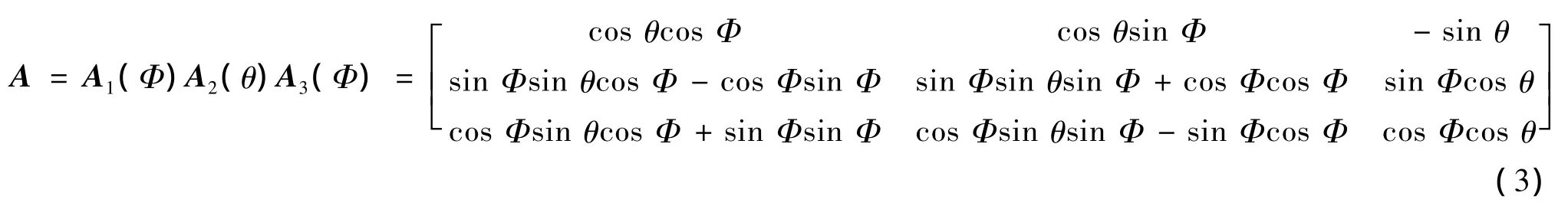
这里采用Z－Y－X欧拉角的矩阵余弦，其中A3(Φ)为绕偏航轴转动Φ，A2(θ)为绕俯仰轴转动θ，A1(Φ)为绕滚动轴转动Φ。

由式(2)计算可以方便地计算出各顶点A符合通电条件的线圈对/永磁体对，同时令转子球体在空间的某一方位角为初始位置，球体的任意步进转动可以由矩阵A∈SO(3)来定义，传感器的输出向量:

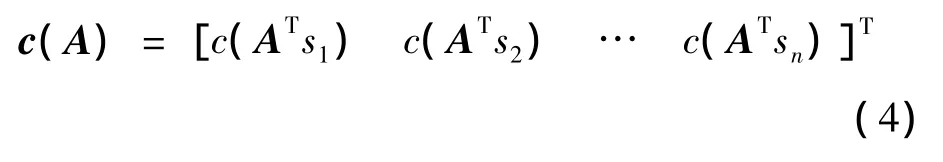
式中:s1，s2，…，sn为n个传感器对应的位置坐标向量，满足{si∈R3;‖si‖=1}。建立闭环控制系统加权有向图各路径的参数如表1所示。

对于点到点复杂的空间运动可以归结为加权有向图中两点间最短路径的求解，经典的Dijkstra寻优算法可以找到最短路径，但需要遍历加权图的各个顶点，这里采用A*启发式算法可以搜索出图中起始点A0到目标点At的最佳路径，首先分别计算这两个顶点对应的输出向量c(A0)和c(At)。

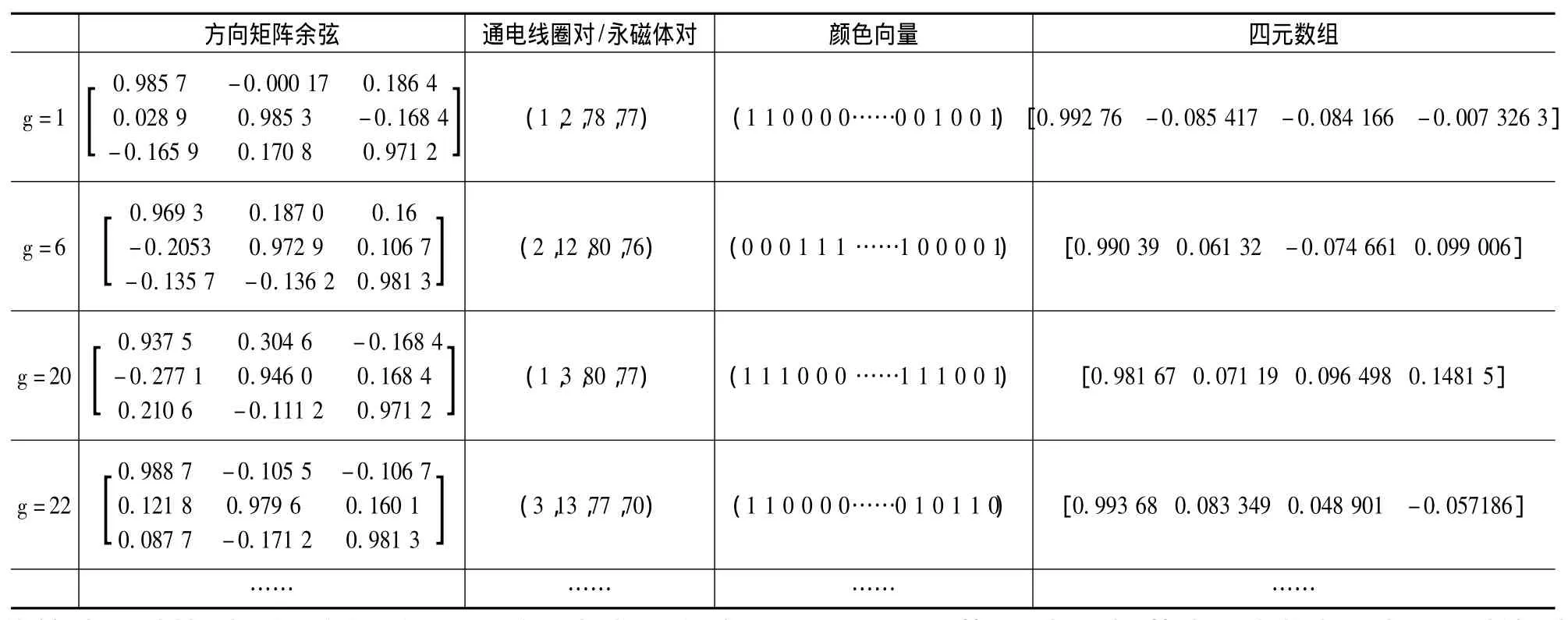
表1 起始点A0的各路径的具体参数

在A算法中设置评估函数f(n):

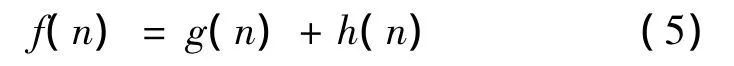
定义:

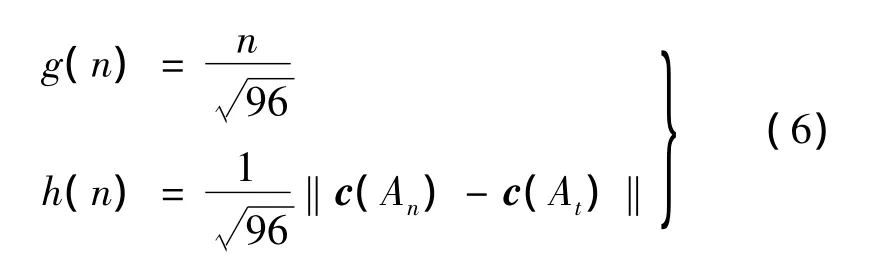
n用来衡量该顶点在图中的深度，搜索路径图时每经由一个顶点的扩展，深度n自动加1。h(n)是顶点An到目的顶点函数代价的估计值，在这里定义为顶点An与目的顶点颜色向量“相异”的元素数量，路径搜索时总选择h(n)最小值的节点优先扩展，所以满足了h(n)≤h*(n)的条件，该算法称为A*算法，h(n)随坐标轴的二维旋转的关系如图3所示。A*算法的可采纳性表明该搜索算法总能找到一条最佳路径，搜索步骤如下:

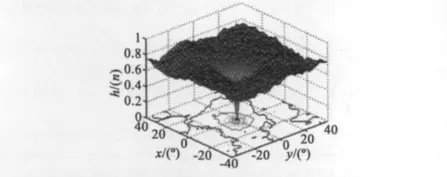
图3 目标函数h(n)与旋转角度的二维关系

(1)设当前节点为初始节点A0，计算该节点的f(n)并放入OPEN表中;

(2)若OPEN表为空，则失败退出;

(3)取出OPEN表中第一顺位节点定义为An节点，计算c(An)，与当前测量值相比较，如有不同表示有串扰，重新进行方位角检测并定位为An节点，放入OPEN表中;

(4)若An为目标节点，则成功退出，否则转到(5);

(5)对An节点进行扩展，若有子节点，则n=n+1，计算各子节点的f(n)，放入OPEN表中，同时将父节点放入CLOSED表中;

(6)若An节点没有子节点，则转(2);

(7)计算An各子节点符合旋转条件的通电线圈对/永磁体对，并对OPEN表按f值以升序排列;

(8)OPEN表中删除当前节点An，转(2)。

3 闭环控制的方法和仿真

球形电机是一个多路径的复杂运动机构，为计算方便，这里分别做了简化处理，令球心坐标为三维坐标原点，球半径为1，加权有向图中球形电机初始方位角下各条路径的参数如表1所示，利用对应的旋转四元数组参数计算路径一各永磁体、线圈的位置坐标如图4所示。

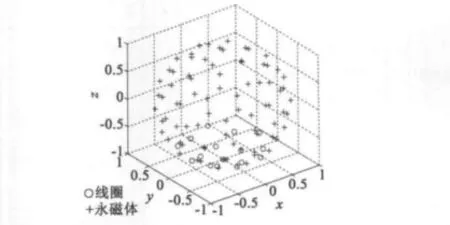
图4 路径－永磁体的新位置

给定一个未知目标节点对应的传感器输出为Cx，建立初始方位角下运动轨迹的加权有向图，按A*算法搜索到目标节点的搜索过程如图5所示，由搜索图可知，A*算法可以跳出局部极值并不需要遍历所有节点，路径上的各项参数如表2所示，任取球面一点坐标为(－0.520 84 0.215 74 0.825 94)，它在搜索到的最佳路径上运动轨迹如图6所示。

在加权有向图的步进运动中或是在最佳路径的搜索过程中，偶有的串扰会偏离预定的轨迹，例如搜索路径中第一条轨迹因串扰的各项参数对照如表3所示。每次步进的运动控制前将光电传感器的输出与有向图数据库中预知路径的传感器输出相比较，不一致时则判定有串扰存在，需要对当前方位角进行重新定位，对于步进运动的串扰而言，角度位移基本都落在图3中的线性区内，此类方位角检测可以采用启发式搜索达到最高的搜索效率［6］，对于偶有的串扰将引起大角度的轨迹偏离，文献［11］已讨论这种情况下的重新定位。

表2 初始方位角下搜索路径的各项参数

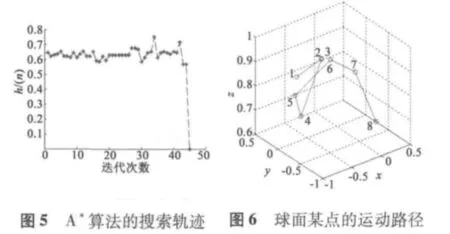
表3 串扰中第一条轨迹的参数对照

启发式搜索对于邻域的搜索效率最高，从顶点开始的搜索轨迹如图7所示。设置esp＜0.15，可看出在第15次迭代时到达目标节点f=0.102 1，由该节点的方位角参数计算出因串扰的实际旋转的四元数组为［0.998 4 0.041 7 0.024 5 －0.028 6］，重新计算该角度下符合步进旋转的23对永磁体/线圈对，如表4所示，并添加到步进轨迹的加权有向图中去。

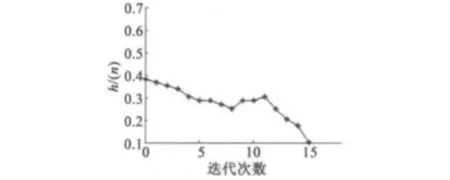
图7 串扰后目标节点的启发式搜索轨迹

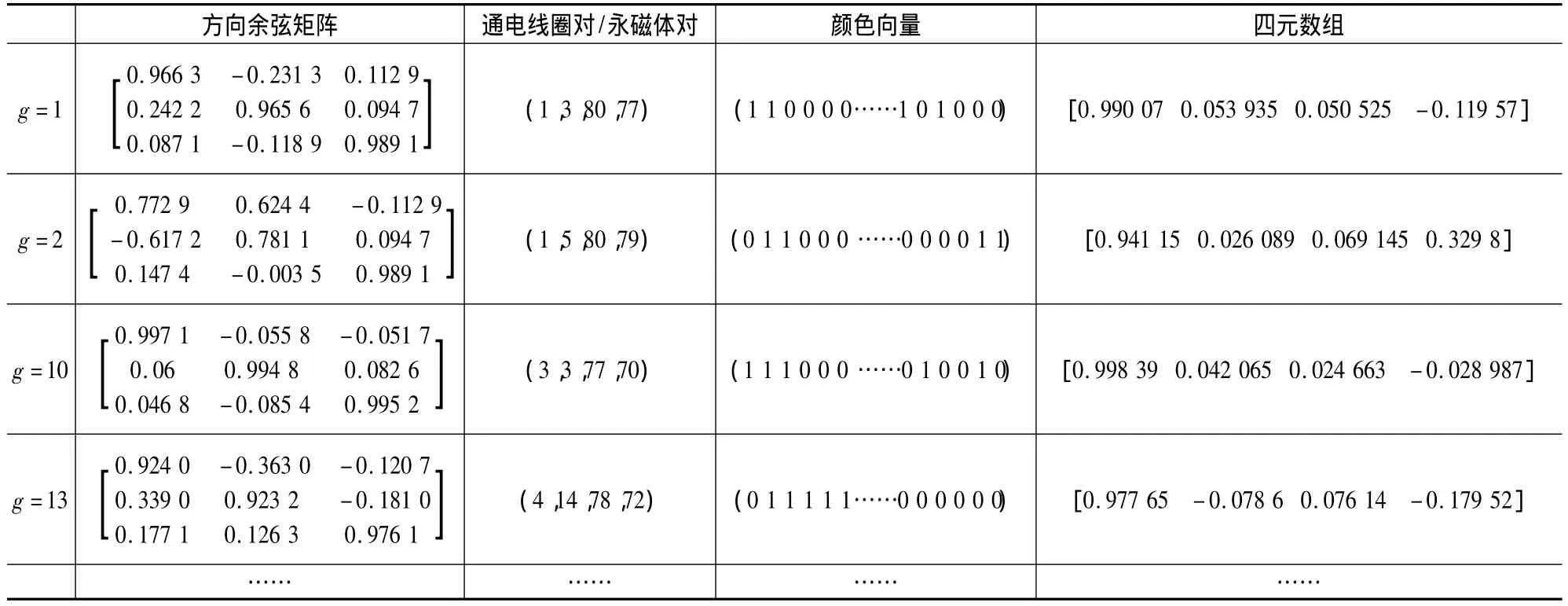
表4 串扰后各路径的具体参数

4 结 语

本文针对球形电机三维空间步进旋转的特点，构建了步进运动的加权有向图，由于运动控制中可能存在串扰会使球形电机偏离预定轨迹，本文将方位角检测算法添加到运动控制中，研究了球形步进电动机的闭环控制方法。仿真表明，A*算法不需要遍历图中所有节点就可以搜索到点到点的最佳路径，且在串扰偏离预定轨迹时，启发式搜索可以快速地寻找到失步的目标节点，从而重新计算永磁体对/线圈对并添加到已有的有向图中去。

［1］Chirikjian G S，Stein D.Kinematic design and commutation of a spherical stepper motor［J］.IEEE/ASME Transactions on Mechatronics，1999，4(4):342 －353.

［2］Stein D，Scheinerman E R，Chirikjian G S.Mathematical models of binary spherical－ motion encoders［J］.IEEE/ASME Transactions on Mechatronics，2003，8(2):234 －244.

［3］Stein D，Chirikjian G S.Experiments in the commutation and motion planning of a spherical stepper motor［C］//ASME Design Engineering Technical Conferences and Computers and Information in Engineering Conference.ASME，2000:10 －13.

［4］吴立建，王群京，杜世俊，等.磁场积分法在永磁步进球形电动机场分析中的应用［J］.中国电机工程学报，2006，26(10):158－165.

［5］王群京，李争，夏鲲，等.新型永磁球形步进电动机结构参数及转矩特性的计算与分析［J］.中国电机工程学报，2004，24(9):192－197.

［6］王群京，雍爱霞，陈丽霞，等.一种永磁球形步进电机转子位置的检测方法［J］.中国电机工程学报，2006，26(22):92－96.

［7］王群京，雍爱霞.永磁球形步进电机转子位置检测的全局优化［J］.中国电机工程学报，2007，27(33):11 －16.

［8］雍爱霞，王群京，倪有源.基于四元数组的球形电机的控制［J］.微电机，2006，39(9):33 －37.

［9］马中骐.物理学中的群论［M］.北京:科学出版社，2005.

［10］张帆，曹喜滨，邹经湘.一种新的全角度四元数与欧拉角的转换算法［J］.南京理工大学学报，2002，26(4):377 －380.

［11］雍爱霞，王群京.基于变尺度混沌搜索的永磁球形电机的位置检测［J］.系统仿真学报，2009，21(15):4722－4725.