向量内外积在直线坐标方位角反算中的应用研究
2015-11-25陆超
陆 超
(重庆交通大学 土木工程学院,重庆 400074)
Lu Chao
(School of Civil Engineering,Chongqing Jiaotong University,Chongqing 400074)
坐标方位角在工程测量应用中具有重要地位。在市政工程、公路工程现场施工放样中,通常采用极坐标法将设计点位放样到实地,必须通过坐标反算得到测站点到放样点的距离和坐标方位角。
传统的坐标方位角计算方法是在象限判断的基础上利用象限角与方位角的定量关系推算坐标方位角,象限角与方位角概念混淆时计算容易出错[1-5]。对目前所有测量书籍和相关资料分析,不难看出,基本上从三角函数关系(标量)的角度分析坐标方位角的计算方法。这些推导过程和计算公式(含统一数学模型)不便于理解与掌握。
本文将向量内积、外积引入到直线坐标方位角的计算公式的推导过程中,为坐标方位角的推算提供一种新思路,同样是对反余弦函数计算坐标方位角做出的新解释。
1 传统的坐标方位角计算法
方位角是指从起始方向北端算起,顺时针旋转至某方向线间的水平角度[6]。根据起始方向的选取不同,方位角具体分为真方位角、磁方位角和坐标方位角。其中,坐标方位角的起始方向为坐标纵线。坐标方位角的取值范围是0°~360°。
在传统的坐标方位角计算中,引入了象限角概念。象限角是指由标准方向的北端(或南端)顺时针(或逆时针)旋转至某一直线的水平锐角。象限角的取值范围是0°~90°。
已知测站点和放样点的坐标分别为A(XA,YA)、B(XB,YB),则两点坐标增量△XAB=XB-XA,△YAB=YB-YA,AB两点距离,象限角RAB为:

坐标方位角与象限角是两种不同的概念,传统的坐标方位角计算方法是基于象限角来进行的。根据△XAB和△YAB的正负性,通过添加常数项将象限角转换为坐标方位角αAB。这种计算方法不仅比较繁琐,而且△XAB为0时需要特殊处理。
2 坐标方位角计算新思路
2.1 坐标方位角与向量夹角关系
距离没有方向性,需要借助X、Y增量的正负性来判断坐标方位角所在象限。然而向量既代表大小,又代表方向,可以直接断定坐标方位角所在象限。选取坐标纵轴(正北方向)的单位向量=(1,0),向量与向量夹角为θ。向量夹角θ∈[0°,180°],而坐标方位角α∈[0°,360°),两者之间存在着某种固定转换关系。各象限中坐标方位角α与向量夹角θ的关系如图1所示。
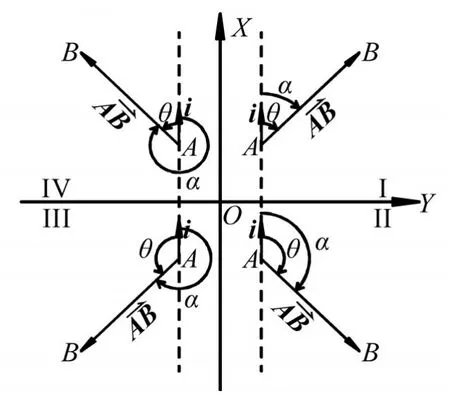
图1 坐标方位角与向量夹角关系
由图1易得,当α在第一、二象限时,α=θ;当α在第三、四象限时,α=360°-θ。其中,θ可由向量内积定义求得,向量夹角θ为:

坐标方位角所在象限判定的定量表达成为问题的关键。从向量角度出发,引入了向量外积[7]。
2.2 向量外积引入

综上所述,直线的坐标方位角α为:

当△YAB=0即位于X轴时,式(4)同样成立。可以将式(4)合并为统一的表达式:

3 结语
从矢量角度出发,借助向量内积、外积推导直线坐标方位角的计算公式,该方法具有形象直观,容易理解和掌握的优点,为进一步理解直线坐标方位角的计算提供一种新思路。内外积分析法同样可用于解决道路路线的转角问题。
[1]谭家兵,刘星.利用坐标反算直线坐标方位角的最佳数学模型[J].江苏测绘,2001,24(3):24-25,27.
[2]高俊强,郑国才.测量学教学中坐标方位角的计算[J].现代测绘,2005,28(5):47-48.
[3]陈德标.坐标方位角计算实用通式[J].测绘通报,2006(2):30-31,69.
[4]王健,李小光,宋利杰.直线坐标方位角的简明算法[J].矿山测量,2010(2):62-63,65.
[5]涂群生.距离和坐标方位角计算的简易方法[J].测绘通报,2006(7):43-44.
[6]郑平元,杨武年,杨容浩.辅助角法在坐标方位角反算中的应用[J].测绘与空间地理信息,2012,35(7):44-45.
[7]李香清.基于对话框编写实现坐标方位角正算与反算的程序[J].城市勘测,2013(5):137-139.
