无轴承同步磁阻电动机解耦控制研究现状

冯冬梅，刁小燕，朱熀秋

(江苏大学，江苏镇江212013)

0 引 言

无轴承电动机没有像传统电机里面轴承与转子之间的摩擦力，高速运行也不需要添加润滑油就能实现，并且具有低噪声和低振动等特点。无轴承电动机把转矩绕组和可以控制转子位置的径向悬浮力绕组放置在同一定子上，使轴承和电机形成一体化结构，转子收到磁场力的支持。无轴承同步磁阻电动机既具有同步磁阻电动机结构简单、重量轻、体积小等显著特点，又具备了磁轴承机械磨损小、无需润滑、无油污染、高速高精等优点，它的优越性能远非传统电动机所能比拟。相比磁轴承支承的电动机，无轴承同步磁阻电动机因为把悬浮力绕组与转矩绕组一起叠绕在定子中，电机结构更加简单小巧，克服了磁轴承支承电动机轴向长度长这一缺点，而且由于不存在与轴承之间的摩擦，无轴承同步磁阻电动机能够实现的临界转速往往比磁轴承电机更高。即使把无轴承同步磁阻电动机与其他种类无轴承电动机相比较，它也具有制造方便、电机体积小、重量轻、控制规律清晰等众多优点。另外，由于电机转子上既没有永磁体也没有励磁绕组，能获得较快的动态响应，更加适合应用于高速场所。

日本东京科技大学的A.Chiba等学者在1990年首次将无轴承技术应用于同步磁阻电动机，设计出空载实验转速达12 000 r/min，输出功率能够达到2.12 kW的样机［1］。紧接着，德国开姆尼斯技术大学的L.Hertel等学者也在前人研究的基础上进一步研究无轴承同步磁阻电动机，其样机输出功率为1.5 kW，在无负载情况下样机的实验转速更是能够高达30 000 r/min［2］。国内无轴承电动机的研究起步比国外晚，作为无轴承交流电机的分支之一，无轴承同步磁阻电动机也逐渐被发展，主要是一些理论上的研究和通过仿真软件分析系统动静态性能。但是，无轴承同步磁阻电动机目前局限于理论层次的分析和在实验室研发样机，还没有真正投入生产应用。在基金支持和团队协作帮助下，江苏大学对无轴承同步磁阻电动机做了相关基础研究，研究内容主要包括样机优化设计、数学模型、多变量非线性解耦控制等。本文将简单介绍无轴承同步磁阻电动机的工作原理和数学模型，并总结国内外在对这个非线性强耦合系统解耦控制方面的研究进展。

1 无轴承同步磁阻电动机工作原理

图1为在空载情况下无轴承同步磁阻电动机转子上产生径向悬浮力的示意图，可以很好地说明悬浮力产生机理。对电机4极励磁绕组Na通以电流产生的磁通记为ψa，对附加2极悬浮力绕组Ny通以电流产生的磁通记为ψy。对悬浮力绕组通以图示电流，它产生的磁场使原来已经达到平衡的磁场受到破坏，即3区气隙磁通减小，1区气隙磁通增大。由于1区磁场得到了增强，转子产生了3区指向1区方向的麦克斯韦力，即图示方向上的悬浮力Fy。与此相似，如果把相反方向的电流通入悬浮力绕组，那么电机转子上会产生沿y轴负方向的悬浮力。另外，如果对无轴承同步磁阻电动机中2极悬浮力绕组Nx通以电流，调节Nx中电流的大小和方向，同样可以产生x轴方向上可控的悬浮力。

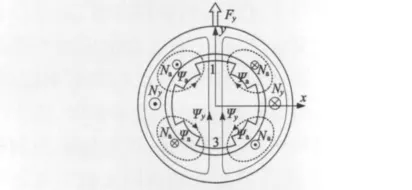
图1 悬浮力产生原理

2 无轴承同步磁阻电动机数学模型

2.1 径向悬浮力模型

无轴承同步磁阻电动机的转子到定子间的气隙长度不相等，导致了气隙磁通密度不均匀，其中磁通密度B与转子机械角θ有关。忽略磁饱和影响，并且假设定子中的三相绕组在空间完全对称分布叠绕，则作用在凸级转子上麦克斯韦力x、y轴方向分量分别为:

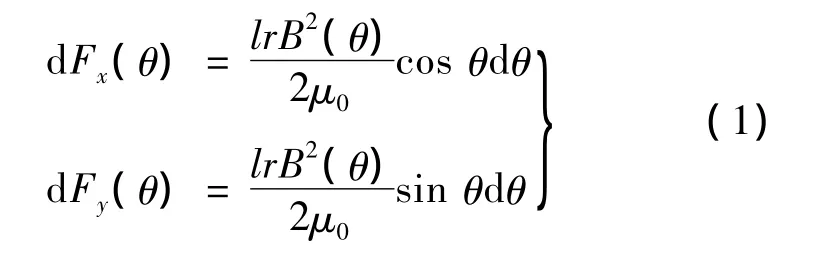
式中:μ0为磁场常数，又称真空磁导率;θ为转子机械角;l为电机转子有效长度;r为凸极处转子半径。

设对电机两套绕组(即转矩绕组和悬浮力绕组)通入电流后产生幅值分别为F1和F2的基波气隙磁动势，空间矢量初始相位角分别为μ和λ。对它们进行矢量相加，可得基波合成气隙磁动势为f(θ)，则有:

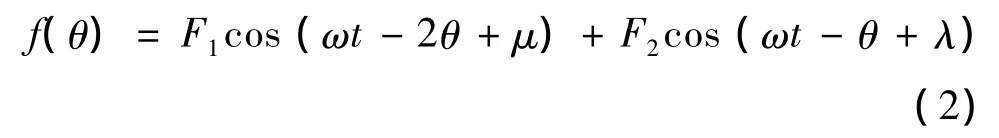
式中:ω为电角频率。

无轴承同步磁阻电动机转子气隙磁通密度与转子凸极处到定子的气隙长度和两套绕组产生的基波合成气隙磁动势有关，其关系式为:

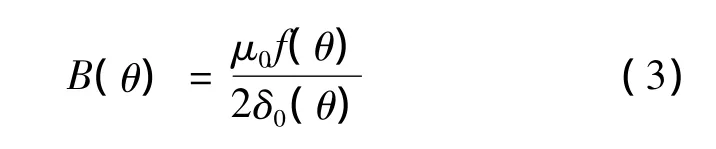
假定转子与定子的偏心位移远远小于电机凸极处的气隙长度，且在计算悬浮力过程中不考虑转子由凸极结构引起的气隙长度的变化，仅以转子凸极处到定子间的气隙计算，此时 δ0(θ)= δ0，将式(2)、式(3)代入式(1)中积分，可以得出转子所受径向悬浮:

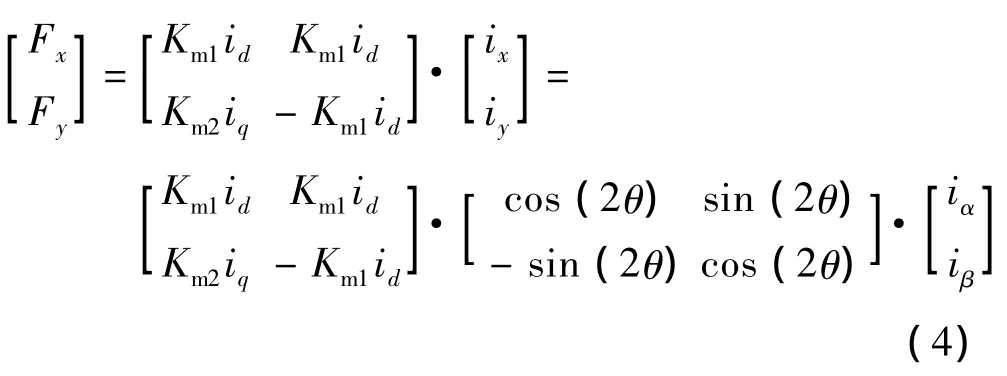
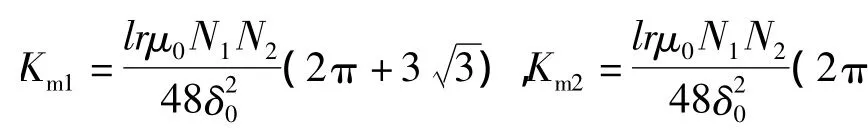
如果定、转子中心点不重合，就会引起转子到定子的气隙长度不等，气隙不平衡，转子上就会产生麦克斯韦力。其具体表达式:

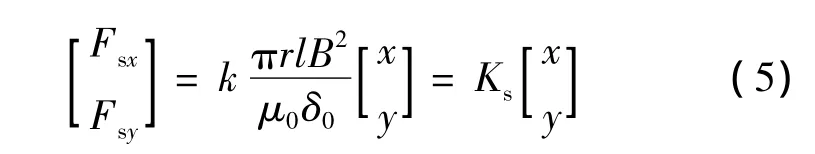
式中:k为衰减比例系数，大小取决电机本体结构的设计，是一个常数;x、y分别为电机转子中心偏离定子中心的位移在水平垂直方向上的分量。

理想状态下，如果在水平、垂直方向上对电机转子(设定自身质量为m)的施加大小分别为Fzx、Fzy的负荷力，对电机转子进行受力分析，可以得到转子的运动方程:

2.2 转矩数学模型

无轴承同步磁阻电动机转子本身没有永磁体，并且直轴方向的气隙磁阻与交轴方向的磁阻并不相等，即ψf=0且Ld≠Lq。转子磁阻转矩产生是由于磁力线会挑一条磁阻最小的路径走，也就是磁阻最小原理。转换到d－q同步旋转坐标系下转矩子系统的数学模型如下:

定子磁链方程:

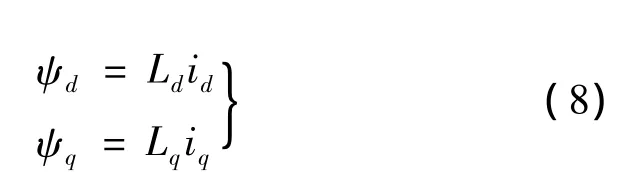
电磁转矩:

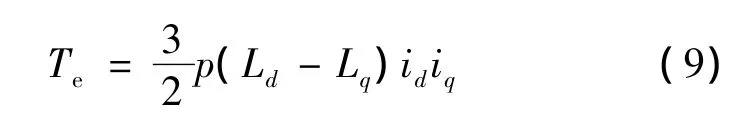
旋转运动方程:

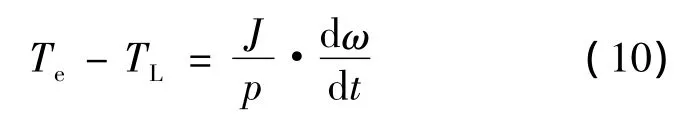
式中:ud、uq为定子电压分量，并且分别是在d、q轴方向上的电压分量;ψd、ψq为定子磁链分量，分别为旋转坐标系下的d、q轴分量;ω为电机定子产生的旋转磁场的角速度;Rs1为定子中的转矩绕组每相电阻阻值;p为电机转矩绕组产生磁场的极对数;J为电机转子转动惯量;Te为电磁转矩，在电机中起拖动作用;TL为负载转矩，在电机中起制动作用。

3 无轴承同步磁阻电动机解耦控制策略

无轴承同步磁阻电动机是一个耦合性非常强，并且具有多输入多输出变量的复杂的非线性系统，转矩绕组和悬浮力绕组各自产生的磁场在气隙中相互叠加在一起导致电磁转矩与悬浮力两者之间相互影响。另外，在垂直和水平方向上，悬浮力自身耦合现象也非常严重，因此，只有完全消除电磁转矩与悬浮力之间还有径向悬浮力自身在x、y方向上的耦合才能使电机悬浮运行在一个稳定状态。综述现有研究成果和文献，其解耦控制策略有以下四种。

3.1 前馈法解耦控制策略

文献［3－7］通过串接前馈补偿器并且给定定子电流的方法，解除了无轴承同步磁阻电动机悬浮力和电磁转矩之间的动态耦合关系。前馈补偿器解耦控制结构图如图2所示，根据悬浮力数学模型推导出公式来证明解耦补偿器可以实现解耦控制。图中，解耦补偿器以转子在x、y轴所受悬浮力的参考值以及转矩绕组d－q轴电流分量id、iq为输入，可以输出大小与相等的径向悬浮力。因此，前馈补偿器可以避免径向悬浮力因为电磁转矩波动而产生变化。但是，由于电机中存在的悬浮力和电磁转矩之间的交叉耦合毕竟是由实际定子电流时变性造成的，所以只有当给定的id恒等于实际的转矩绕组电流d轴分量时，被控对象才能成功解耦。但是由于电机本身负载为感性，存在滞后环节，所以电机刚开始起动或者负载发生大小变化等过程中，给定定子电流并不恒定等于实际的定子电流，可能造成解耦不成功。另外，受磁饱和因素的影响，解耦补偿器中的参数容易发生变化，因此并不能实现电磁转矩和径向悬浮力之间完全意义上的动态解耦。

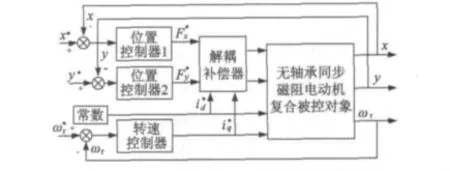
图2 前馈补偿器解耦控制结构图

3.2 反馈解耦控制策略

在前馈补偿解耦的基础上用转矩绕组d轴电流反馈量取代给定定子电流参与解耦运算，就是反馈解耦控制方法。文献［8－10］通过添加反馈补偿的方法来实现对无轴承同步磁阻电动机的解耦控制。反馈解耦控制器的结构与前馈补偿器相似，图3为反馈解耦控制结构图。不同的是，反馈解耦控制器中输入量之一采用的是无轴承同步磁阻电动机复合被控对象输出再经过坐标变换的电流反馈值，而前馈补偿解耦控制方法中用给定的励磁电流分量id直接参与运算，这会引起系统准确性和动态性能不佳。反馈解耦控制方法采用反馈回来的励磁电流分量正好克服了前馈法解耦控制准确性和动态性能上的弊端，从而能够成功解耦。但同样因为电机本身存在滞后环节，检测到的电流大小并不一直等同于实际定子电流，所以在转速大幅度调节或负载突然发生变化等快速响应过程中解耦还是有可能失败。

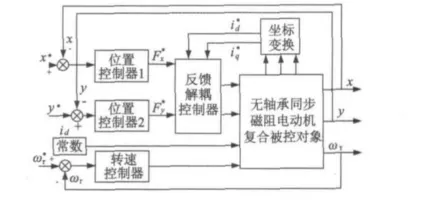
图3 反馈解耦控制结构图

3.3 逆系统解耦控制策略

文献［11－16］将α阶逆系统理论应用于强耦合、多变量的非线性无轴承同步磁阻电动机系统，从而把无轴承同步磁阻电动机系统线性化解耦成为三个线性积分子系统，并且三个子系统之间相互独立。图4是α阶逆系统解耦图，图中把位置和转速控制器串联在α阶逆系统之前，组成了逆系统复合控制器，以给定值与反馈值的差值为输入信号，输出转矩电流分量参考值，悬浮力绕组x－y轴电流分量参考值与给定励磁电流分量值id一起作为无轴承同步磁阻电动机复合被控对象的输入值。逆系统方法能够有效提高系统的控制性能，而且能完全意义上解除无轴承同步磁阻电动机变量之间的耦合。但是逆系统方法需要能够精确描述被控系统的非线性输入输出特性，建立准确的数学模型，显然这些在实际工程问题中难以实现。而且由于实际工业模型比较复杂，即使能够建立被控非线性系统的精确数学模型，如何准确解出逆系统又是个难题。这些问题阻碍了逆系统方法的进一步发展，极大地限制了它的使用。

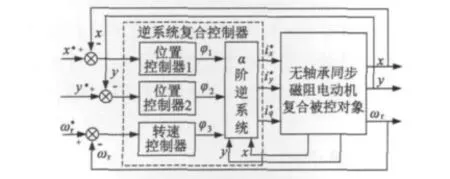
图4 α阶逆系统解耦图

3.4 支持向量机逆系统解耦控制策略

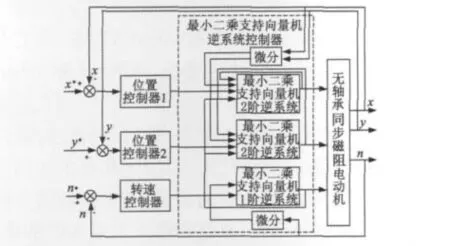
图5 基于最小二乘支持向量机逆系统的复合控制

对于无轴承同步磁阻电动机这个具有多输入输出变量，而且又有强耦合性质的非线性系统，目前使用的矢量解耦控制方法中存在众多问题，比如计算过程复杂、参数变化常常能够引起控制性能不佳等。而逆系统解耦控制方法也存在建立数学模型困难、求逆模型解析解运算量大等缺陷。为实现其电磁转矩和悬浮力之间的解耦控制，文献［17－20］提出了最小二乘支持向量机逆系统解耦控制方法，这是一种比较新颖的解耦控制策略，图5是支持向量机逆系统控制结构图。把逆系统方法与支持向量机思想有机结合起来就能实现支持向量机逆系统解耦控制。与逆系统等方法相比，最小二乘支持向量机不需要建立精确的数学模型，克服了前面三种方法精确数学模型难以建立而引起的系统准确性不高的缺点，这种优越性决定了支持向量机逆系统解耦控制策略能够广泛应用于非线性解耦控制。这种控制策略首先推导在非线性连续系统下最小二乘支持向量机逆模型算法，并将该算法应用到无轴承同步磁阻电动机这个耦合性极强的多输入输出变量连续系统中，通过系统微分方程的输入输出特性分析，将原先复杂的强耦合连续系统解耦成三个具有线性传递函数关系并且互不影响的伪线性单输入单输出(SISO)子系统。由于伪线性系统并不是真正意义上的线性系统，所以必须在此基础上设计闭环控制器，最后通过仿真试验验证得出这种控制方案能正确可靠解耦。

4 结 语

无轴承同步磁阻电动机励磁调节简单，容易实现高速运转，而且其控制规律清晰、性能优良，所以能够在高速电力传动场所中脱颖而出，同时在特殊环境比如航空航天、食品生产等场所也有着很大的使用价值。但是目前在无轴承同步磁阻电动机发展的道路上还有很多亟待解决的实际应用问题，导致了它并没能真正运用于工业生产。优化设计控制系统是无轴承同步磁阻电动机研究的重中之重，由于电机本身参数容易因为各种原因发生变化，很多解耦控制方法的准确性有待提高，如果能采用滑模变结构控制、自适应控制等新颖的控制算法和解耦控制策略，来实时跟踪时变参数从而减少解耦效果对于电机参数的依赖性，整个控制系统的稳定性和准确性必然能得到进一步提高。另外，将逆系统方法或者其它反馈线性化方法与智能控制方法相结合并取长补短，是解耦控制今后的重要研究方向之一。因此，对于无轴承同步磁阻电动机解耦控制方法的研究是一个十分迫切且兼具现实和长远意义的重要课题。

［1］Chiba A，Chida K，Fukao T.Principles and characteristics of a reluctance motor with windings of magnetic bearing［C］//Proc.of 1990 IPEC，Tokyo.1990:919 －926.

［2］Hertel L，Hofmann W.Theory and test results of a high speed bearingless reluctance motor［C］//Proc.of 1999 PCIM，Nuremberg.1999:143－147.

［3］Chiba A，Azizur Rahman M，Fukao T.Radial force in a bearingless reluctance motor［J］.IEEE Trans.on Magnetics，1991，27(2):786－790.

［4］Michioka C，Sakamoto T，Ichikawa O.A decoupling control method of reluctance－type bearingless motors considering magnetic saturation［J］.IEEE Trans.on Industry Applications，1996，32(5):1204－1210.

［5］Hertel L，Hofmann W.Magnetic couplings in a bearingless reluctance machine［C］//Proc.of 2000 ICEM，Helsinki.2000:1776 －1780.

［6］Zhang Hannian，Zhu Huangqiu，Zhang Zhibao，et al.Design and simulation of control system for bearingless synchronous reluctance motor［C］//Proc.of 2005 ICEM，Nanjing.2005:554 －558.

［7］张汉年，朱熀秋，张植保.基于前馈补偿器的无轴承同步磁阻电机解耦控制［J］.东南大学学报，2005，35(增刊Ⅱ):193－197.

［8］Zhang Hannian，Zhu Huangqiu，Diao Xiaoyan.Feedback decoupling control of bearingless synchronous reluctance motor［C］//26th Chinese Control Conference.2007:763 －767.

［9］Lv Yanbo，Diao Xiaoyan，Zhu Huangqiu.State feedback decoupling control of AC 5 degrees of freedom hybrid magnetic bearings［C］//Proc.of 2011 ICEMS.2011:1 －5.

［10］张汉年，朱熀秋，刁晓燕.无轴承同步磁阻电动机反馈解耦控制［C］//第26届中国控制会议论文集.2007(4):763－767.

［11］王喜莲，葛宝明.磁浮开关磁阻电机径向悬浮逆系统方法控制［J］.电机与控制学报，2009，13(3):356 －360.

［12］张兴华，戴先中，基于逆系统方法的感应电机调速控制系统［J］.控制与决策，2000，15(6):708 －711.

［13］Ronald M Hirschorn.Invertibilty of multivariable nonlinear control systems［J］.IEEE Trans.on AC，1979，24(6):855 －865.

［14］Sahjendra N Singh.Decoupling of invertible nonlinear systems with state feedback and precompensation［J］.IEEE Trans.on AC，1979，24(6):1237 －1239.

［15］张婷婷，朱熀秋.无轴承同步磁阻电机逆系统的解耦控制［J］.控制理论与应用，2011，28(4):545 －550.

［16］孙晓东，朱熀秋.基于神经网络逆系统理论无轴承异步电动机解耦控制［J］.电工技术学报，2010，25(1):43 －49.

［17］Alex J Smola.A tutorial on support vector regression［J］.Statistics and Computing，2004，14(3):199 －222.

［18］曹克强，胡良谋，李小刚，等.非线性系统的支持向量机逆模型辨识及控制［J］.机械科学与技术，2011，30(5):708 －711.

［19］周云红，孙玉坤，黄永红.磁悬浮开关磁阻电机的支持向量机逆全解耦控制［J］.江苏大学学报，2012，33(1):60 －64.

［20］Vapnik V N.An overview of statistical learning theory［J］.IEEE Trans.on Neural Networks，1999，10(5):955－999.