微型直流电动机电枢电流提取新方法

黄传金，宋海军，陈铁军，李观文

(1.中州大学，河南郑州450044;2.郑州大学，河南郑州450001;3.96520部队，河南洛阳471000)

0 引 言

由于直流电动机换向和反电动势脉动原因，直流电动机电枢电流的电气参数包含有转速信息，而转矩和转速的增量成正比。基于此，利用电枢电流的电气参数间接求取直流电动机的机械特性成为可能［1－5］。

由于直流电动机换向是个复杂的过程，很难做到直线换向，存在延迟换向和超前换向的现象，文献［1］采用LC谐振选频电路获取换向脉冲信号以及将其用于抑制火花干扰脉冲，但转速范围较大时，LC很难及时跟踪选频。文献［2－3］采用电流互感器取样，利用LabVIEW软件的FFT变换获取稳态时的频率，由于是求取稳态特性，不需要转速等于零的电气信息，所以没用滤波电路，但该方法不能获取直流电动机的起动特性。考虑直流电动机起动时的信号是非线性、非平稳信号，文献［4］采用小波滤波器滤除噪声分量，但由于采用了离散小波变换，很容易丢失高频信息［5］。为此，文献［5］提出小波包变换的浮动阀值去噪算法，做到既去除了噪声，又减少信号高频信息的损失，但其本质上也是小波理论。随着对小波理论的深入研究，发现有以下缺点:(1)受Heisenberg测不准原理的制约［6］;(2)小波基函数选取比较困难，没有成熟的理论;(3)一旦小波分解层数确定，其频率分辨率也就恒定，缺乏自适应性。

针对小波理论在分析非线性、非平稳信号方面的不足，2005年Smith在前人研究的基础上提出一种新的自适应的信号分析方法－局部均值分解(以下简称LMD)［7］。LMD已成功用于脑电信号分析和机械故障诊断等领域［8－10］，但在电机测试领域的研究工作还未见报道，本文将其用于微型直流电动机测试信号的去噪处理。

1 局部均值分解原理［8－9］

LMD可将非线性、非平稳信号分解为若干具有一定物理意义的PF(product function)分量之和，该PF分量由纯调频函数与包络函数相乘得到。对任一信号 x(t)，相应的分解步骤如下［8－10］:

(1)设ni为信号x(t)的局部极值点，mi为任意两个相邻的局部极值点的平均值，则有:

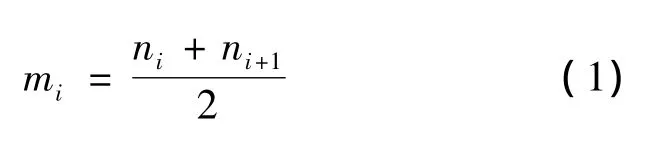
将式(1)中所有相邻的局部均值点mi和mi+1用折线连接起来，然后用滑动平均法对其进行平滑处理，得到局部均值函数m11(t)。

(2)包络估计值ai:

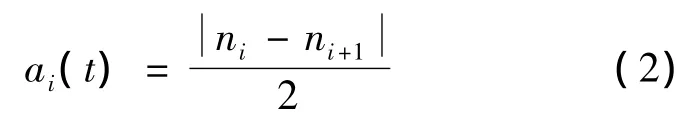
和求取局部均值函数m11(t)的方法类似，将ai和ai+1连接起来并用滑动平均法进行平滑处理，便可得到包络估计函数a11(t)。

(3)用x(t)减去局部均值函数m11(t)可得到信号h11(t)，即:

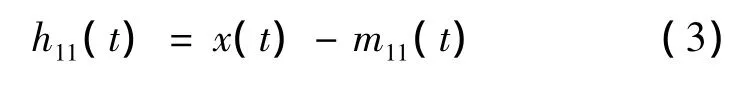
(4)调频函数s11(t)可由h11(t)除以包络估计函数得到，即:

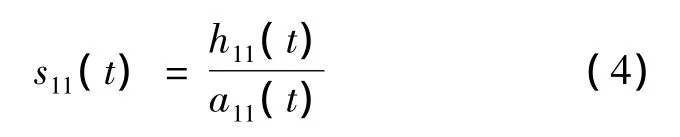
将调频函数s11(t)作为原始信号重复以上过程，可得到s11(t)的包络估计函数a12(t)。假如a12(t)不为1，表明s11(t)不是纯调频函数，则将上述迭代过程重复n次，至 s1n(t)为纯调频函数时结束，即s1n(t)的包络估计函数a1(n+1)(t)=1，故有:

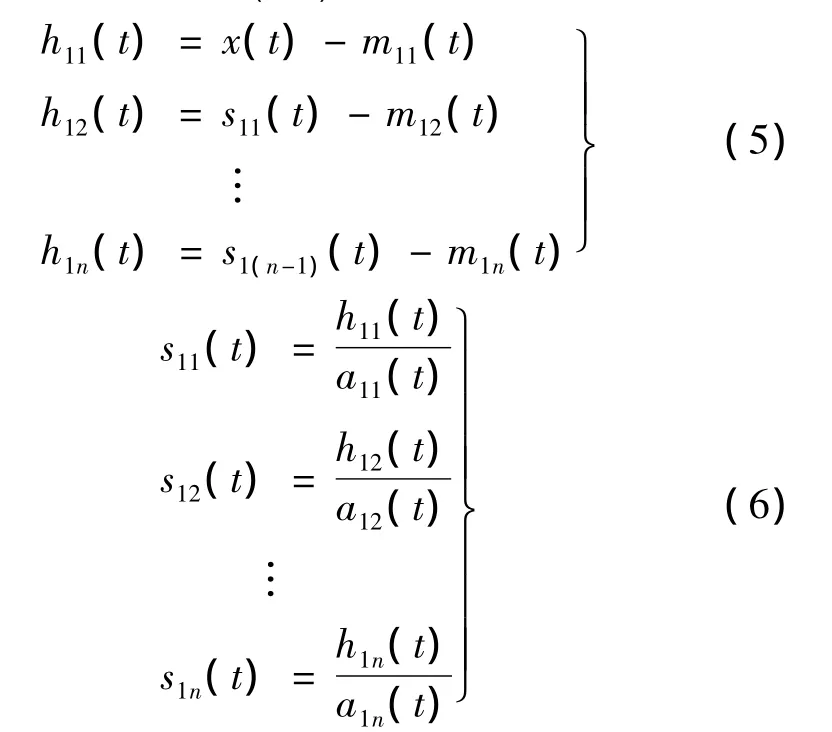
迭代终止的条件:

(5)包络信号a1(t)由所有包络估计函数的积组成，即:

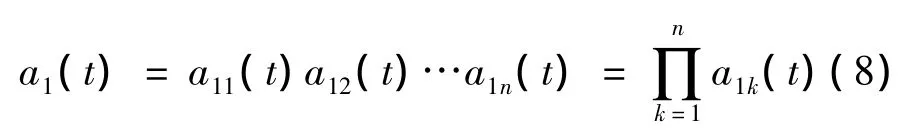
(6)原始信号x(t)的第一个PF分量由纯调频函数s1n(t)与包络函数a1(t)相乘得到:

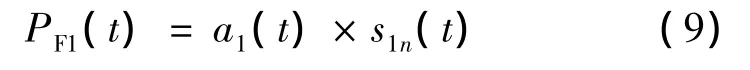
(7)原始信号x(t)减去PF1(t)分量，便得到u1(t)，将u1(t)作为新的信号重复上述过程循环k次，至uk(t)为单调函数时为止。

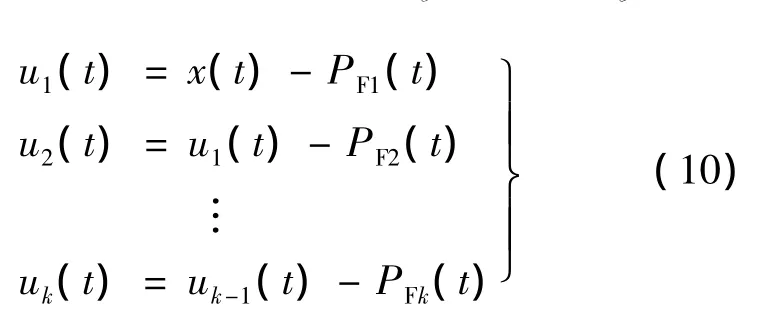
从上述过程可知，原信号x(t)可以由uk(t)和所有PF分量重构，即:

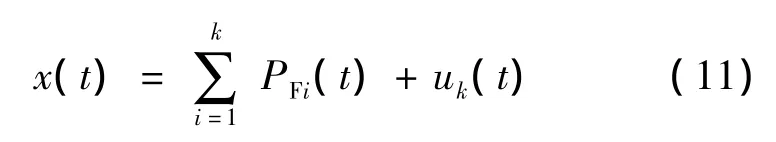
2 微型直流电动机测试电流信号采集系统

常用的电流信号采样有电阻采样法、电流互感器采样法和霍尔电流传感器采样法。由于电阻采样法改变了电枢阻值，而且整个电路的抗干扰能力下降，故不宜采用;电流互感器法的通频带较窄，转换精度较低，而微型直流电动机的电枢换向电流信号很小，也不易采用;霍尔电流传感器具有良好的电磁隔离效果，而且转换精度高、通频带宽和温漂小等特点，本文选用LEM公司的LSTR25N型霍尔电流传感器，该型号基于磁平衡原理设计，具备差分输出功能，次边和原边线圈匝数比为2 000，线性度为0.1%，取样电阻为50 Ω，带宽为DC－200 kHz。其他实验设备还包括阿尔泰公司的ARTUSB2850数据采集卡、实验电源和微型永磁直流电动机ZYTD－50SRZ－R，具体组成如图1所示。

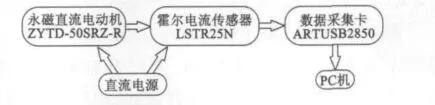
图1 直流电动机电枢电流信号采集系统

图1 中，直流电动机的空载电流为0.18 A，空载转速为2 000 r/min;UN=12 V，PN=15 W，IN=1.25 A;其极对数为1，换向片数为12。ARTUSB2850数据采集卡采样频率可达500 kHz，内置的模拟输入转换芯片为16位的AD7665ASTZ，模拟输出转换芯片为12位的 AD5725，测量精度为0.01%，ARTUSB采集的信号保存格式为.usb，经阿尔泰提供的二次转换软件将.usb转换为.txt格式以便进一步处理分析。数据处理软件使用Matlab2011a。采集的起动电流信号如图2所示(采样频率为20 kHz)，LSTR25N二次侧的电压波形如图3所示。

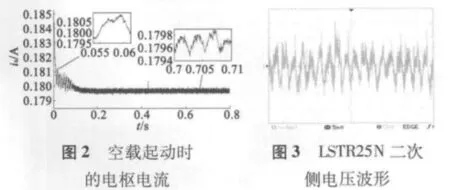
由图2局部放大图和图3对比可知，本文的实验较好地采集了电枢电流信号;由图2和图3还可看出，采集的信号在起动瞬间和稳态运行都有较多的噪声干扰成分，通过求取信号的频率以便得到转速信息，但还要滤除干扰。

3 基于LMD的电枢电流提取新方法

3.1 电枢电流含有噪声的原因

直流电动机换向是个复杂的电磁、化学和机械过程。一般认为电枢的反电动势(换向电势)等于电抗电势(线圈自感电势和互感电势)时直流电动机是直线换向，反电动势大于电抗电动势时延迟换向，反电动势小于电抗电动势时超前换向。电机在实际运行中，电抗电势的瞬时值很难计算，其值还与电刷和换向片的接触电阻有关，因此直流电动机在换向时存在延迟换向和超前换向，而延迟换向和超前换向会带来高频毛刺噪声;换向器表面的氧化亚铜薄膜对电机的良好换向也有重大作用，如果电刷压力过大，氧化亚铜薄膜受到破坏，也容易引起噪声信号;另外，转子和电刷装置等方面的缺陷都可能导致电刷与换向器接触不良或发生振动而产生火花，引起了高频噪声信号。在采集过程中霍尔传感器的温漂、直流电源的扰动及数据采集卡的零点漂移也会引起噪声信号。

3.2 LMD在电机测试信号滤波中的应用

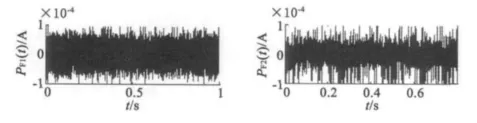
原始信号经LMD自适应地分解得到的PF分量按频率从大到小的顺序排列，而且其幅值成分也反映了信号能量的大小。结合直流电动机电枢电流噪声信号频率最大能量最小、换向电流频率次之能量较大和直流成分频率最低能量最大的特点，选择不同的PF分量，即可得到去噪后的电枢电流、换向电流和直流分量。将图2中的电枢电流用LMD分解得到的PF分量，如图4所示。

从图4中可以看出，PF1和PF2分量的幅值小、频率高，是噪声分量;将PF3至uk(t)相加可得到滤除高频噪声后的电枢电流波形如图5所示;图6为小波阀值消噪后的电流波形;从图4中还可直观看出，PF3至PF5分量具有幅值稍大、频率较高的特点，可认为是换向电流，对PF3至PF5的分量求和即可提取换向的高频电流，如图7所示;从PF6分量开始频率变小逐渐成直流分量，为了直观观察LMD的滤波效果，将PF6至uk(t)的信号相加得到的电枢电流直流成分，如图8所示。

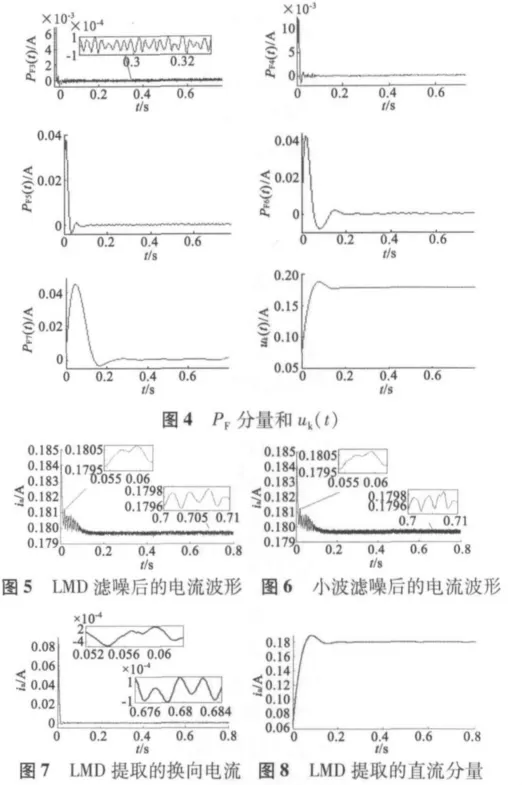
对比图5和图6及其局部放大图可知，在起动瞬间和稳态运行时电枢电流经LMD消噪后的波形都比采用小波消噪后的波形平滑，由此验证了本文所提滤波方法的正确性。对比图1和图7以及图2和图8可以发现，采用LMD的方法不仅能滤除高频噪声信号，还可以有效地提取电枢电流的直流成分及其换向电流。从图5和图7局部放大图可知，换向电流频率约为375 Hz，根据永磁直流电动机ZYTD的极对数和换向片数，将换向电流的频率代入文献［4］中的公式求得转速为1 875 r/min，实验中本文采用闪光测速仪DM6234P+测得稳态转速为1 876 r/min，这也间接说明了本文所提的直流电枢电流提取方法的正确性。

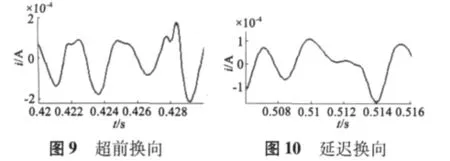
另外，电机换向时的电流大小受反向电动势的影响，主极极靴下的气隙磁场的密度大，相应的反向电动势也大，所以换向电流的幅值较大;主极极靴外的气隙磁场的密度小，相应的反向电动势也小，对应的换向电流的幅值较小。由本文实验波形中的局部放大图可知，高频换向电流的幅值不相等，而是有规律的变化;在本文提取的换向电流信号中发现有超前换向和延迟换向的现象(如图9、图10所示)。这些实验现象也间接验证了本文所提方法的正确性。

4 结 语

本文提出了一种直流电动机电枢电流提取新方法，和采用小波变换的方法相比，LMD方法滤波后的电流波形更平滑，其滤波效果明显优于小波阀值滤波的方法，而且LMD方法还可获取高频换向电流和电枢电流的直流成分。更重要的是，LMD方法具有很强的自适应性，具备良好的推广前景，为直流电动机电枢电流的提取提供了一种新的途径。

［1］陈雅文.直流微电机测速新方法［J］.微电机，1999，32(1):36 －37.

［2］袁宝国.微型直流电动机无传感器测速的虚拟仪器设计［J］.微特电机，2006，34(11):44 －45.

［3］袁宝国.周政新，胡志华.直流电动机无传感器测速实验方法［J］.微特电机，2007(11):21 －23.

［4］黄进，黄建华，陈暾，等.基于小波分析的直流电机转矩－转速特性测试［J］.中小型电机，2001，28(2):49－53.

［5］魏云冰，黄进，黄建华.基于小波包变换的电机测试信号去噪处理［J］.电工技术学报，2001，16(5):64 －67.

［6］Aller J M ，Habelter T G，Harley R G.Sensorless speed measurement of AC machines using analytic wavelet transform［J］.IEEE Transactions on Industry Applications，2002，38(5):1344 －1350.

［7］Smith J S.The local mean decomposition and its application to EEG perception data［J］.Journal of The Royal Society Interface，2005，2(5):443 －454.

［8］朱晓军，樊刘娟，吕士钦，等.LMD方法在脑电信号处理中的应用研究［J］.计算机科学，2012，39(2):273 －275，313.

［9］程军圣，张亢，杨宇.局部均值分解方法及其在滚动轴承故障诊断中的应用［J］.中国机械工程，2009，20(22):2711 －2717.

［10］程军圣，杨怡，张亢，等.基于局部均值分解的循环频率和能量谱在齿轮故障诊断中的应用［J］.振动工程学报，2011，24(1):78－83.