如何用SAS软件正确分析生物医学科研资料XXIV.结果变量为多值有序变量的高维列联表资料的统计分析与SAS软件实现(二)
2013-06-08鲍晓蕾王小利胡良平
鲍晓蕾,王小利,胡良平
对于结果变量为多值有序变量的高维列联表资料可使用cmH 校正的秩和检验或有序变量多重 logistic 回归分析等统计分析方法。在上一期中,我们已经详细介绍了CMH 校正的秩和检验。本期将详细介绍多值有序变量的logistic 回归分析。
1 原理
结果变量为多值有序变量的 logistic 回归又称为累计logistic 回归。累积 logistic 回归模型可视为二值变量logistic 回归的扩展,其回归模型可定义如下:

其中y* 表示观测现象的内在趋势,不能被直接测量;ε为误差项。当结果变量有J个可能的结局,相应的取值为y= 1、y= 2 ……y=J时,共有J– 1 个分界点将各相邻类别分开。即:
若y* ≤μ1,则y= 1;
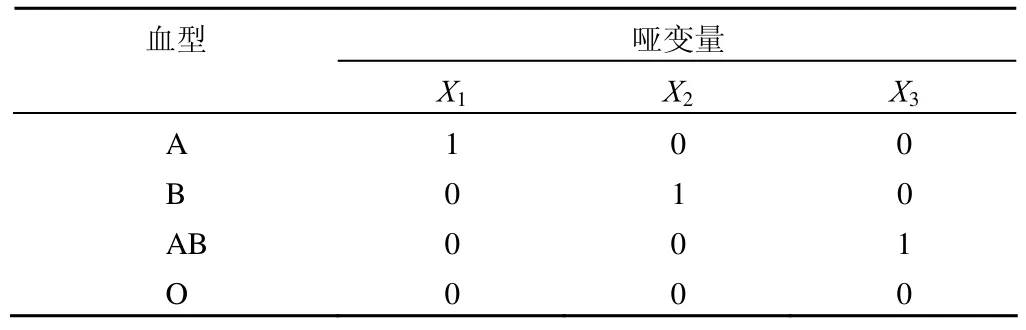
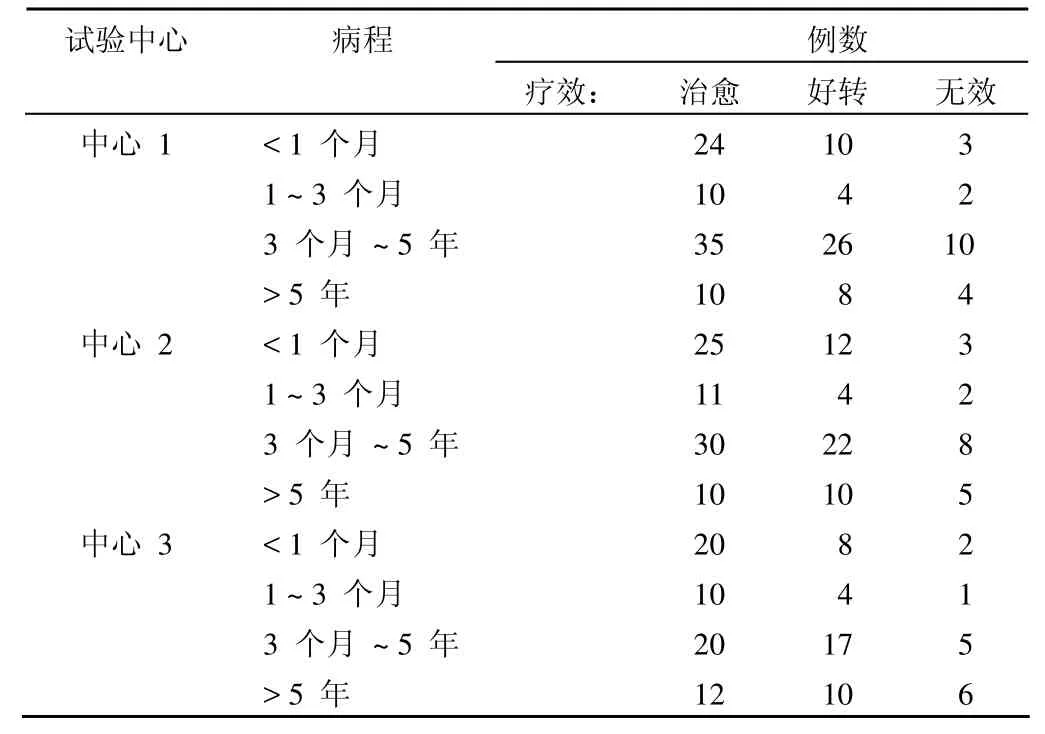
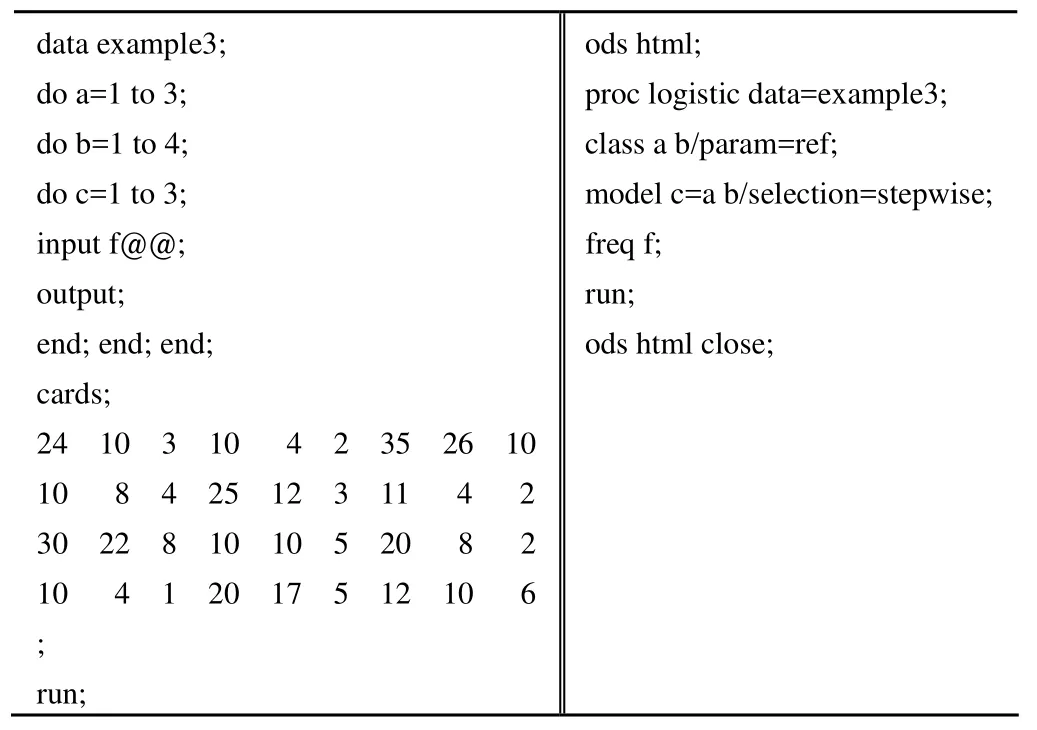
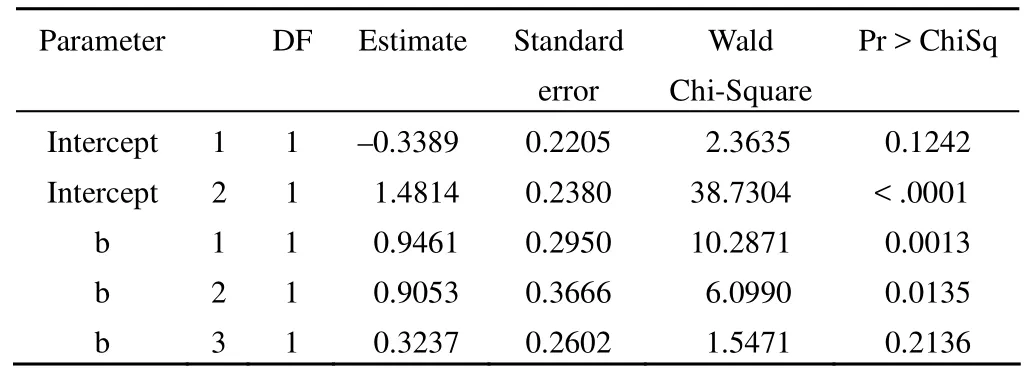
若μ1 …… 若y* >μJ–1,则y=J。 给定x值的累积概率可以按如下形式表示: 与二值变量的 logit变换相似,累积 logit 变换定义如下: 其中 1 –P(y≤j|x) 即为P(y≥j+ 1 |x),这样就依次将J个可能的结局合并成两个,从而进行 logistic 回归分析。 相应地,累积概率可通过以下公式进行预测: 统计软件在实际运行中,定义β0j为各类中截距α与分界点μj的综合,所以上式就转化为: 值得注意的是,SPSS 和 SAS 在对累积 logistic 回归模型进行参数化时采用的形式是不同的,SPSS 软件中采用的线性形式是,这与式 ⑸ 相同,而 SAS 中采用的是,所以式 ⑸ 就转化为: 在使用不同软件时,应该注意回归系数符号的差别。 由上面的讨论可以看出,若结果变量有J个可能的结局,则可获得J– 1 个累积 logit 函数(当进行统计分析时,若有m个截距项β0j无统计学意义,则只能获得J–m– 1 个累积 logit 函数)。累积 logistic 回归模型对每一个累积 logit 函数各有一个不同的β0j估计,然而对所有的累积 logit 函数,变量xk却有一个相同的βk估计,因为其假设条件为自变量的作用与所有累积 logit 的截断点无关。在此假设条件下,不同累积对数发生比的回归线相互平行,只是截距参数有所不同。这被称为成比例发生比假设条件或平行线假设条件。 运用累积 logistic 回归模型首先需要对平行线假设条件进行检验。如果这一假设条件被拒绝,便说明自变量xk对不同的 logit 有不同的βk,因而说明累积 logistic 回归模型不适合,需要采用其他模型来进行资料的分析,如可在模型中引入二次项或交互项。 在 logistic 回归模型中,原因变量可以是连续型变量,也可以是二值变量、多值有序变量或多值名义变量。 如果原因变量是连续变量,一般不需要进行处理,可直接建立 logistic 回归模型。但有时根据专业知识需对其进行分级以获得更有实际意义的结果时,连续变量就转换成了有序变量,此时可按影响结果变量由小到大的顺序赋值为1、2 ……,并将它当作连续型变量处理或直接引入哑变量,建立 logistic 回归模型。比如在肺癌危险因素的病例-对照研究中,研究者往往感兴趣的是年龄每增加 5 岁(根据专业知识和试验目的决定)肺癌发病的危险性是基础状态时的多少倍,而年龄每增加 1 岁肺癌发病的危险性是基础年龄时的多少倍往往没有多大实际意义。 如果原因变量是二值变量,一般可按 0、1 赋值。 如果原因变量是多值名义变量,需引入哑变量(dummy variable),每个哑变量都是一个二值变量,所需哑变量的数目为多值名义变量的类别数减 1。如“血型”是一个多值名义变量,有 A、B、AB、O 四种,若以 O 型血为基准,需引入 3 个(4 – 1 = 3)哑变量来描述。令 则可得到下面的对应关系(表1): 表1 用 3 个哑变量描述一个四值名义的血型变量 如果原因变量是多值有序变量,一般可按影响结果变量由小到大的顺序赋值为1、2 ……,并将它当作连续型变量处理,但这样做有时并不科学,因为该有序变量每上升或下降一个等级对结果变量的影响并非总是“线性”的。若遇到有序原因变量按连续变量处理所得回归效果不理想时,建议引入哑变量的方式来处理。 结果变量为多值有序变量,可按其程度或一般默认的顺序由小到大地赋值为1、2 ……。 【例 1】在一项临床试验中,研究病程与依沙酰胺疗效的关系。试验在三所医院中同时进行,具体疗效数据见表2,试对病程与治疗效果之间的关系进行分析。 表2 病程与依沙酰胺疗效的数据 SAS 程序如下,程序名为example3。 data example3;do a=1 to 3;do b=1 to 4;do c=1 to 3;input f@@;output;end; end; end;cards;24 10 3 10 4 2 35 26 10 10 8 4 25 12 3 11 4 2 30 22 8 10 10 5 20 8 2 10 4 1 20 17 5 12 10 6;run;ods html;proc logistic data=example3;class a b/param=ref;model c=a b/selection=stepwise;freq f;run;ods html close; 程序说明:首先建立数据集,程序中的 a 表示试验中心,a = 1 表示中心 1,a = 2 表示中心 2,a = 3 表示中心 3;b 表示病程,b = 1 表示 < 1 个月组,b = 2 表示 1~3 个月组,b = 3 表示 3 个月~5年组,b = 4表示 > 5年组;c 表示疗效,c = 1 表示治愈,c = 2 表示好转,c = 3 表示无效;变量 f 表示频数。调用 logistic 过程进行有序变量多重 logistic 回归分析。由于试验中心是多值名义变量,需对其赋哑变量;病程是多值有序变量,可将其当成连续型变量直接赋值,但最好是对其赋哑变量。若自变量是二值变量,则只需直接赋值 0、1 即可。class 语句可实现对自变量自动赋哑变量,同时还能保证哑变量在回归方程中同进同出。class a b 表示对 a、b 两个因素均自动赋哑变量。选项param = ref 指定将其中的一个水平作为基准实现哑变量赋值,默认以输入的该定性变量最后一个水平为基准。若想以其他水平为基准,比如希望以 a 的第一个水平为基准对因素 a 赋哑变量,则只需将语句改成 class a (ref = ‘1’)b/param = ref 即可。model 语句表示建模,等号前表示因变量,等号后表示自变量。选项 selection = stepwise 表示用逐步回归法进行变量筛选,其默认的进入和剔除方程的显著性水准为0.05;若希望改变这一标准,可在选项后加入 sle =xx 和 sls = xx 选项,前者指定进入方程的标准,后者指定剔除方程的标准,xx 表示具体的数值(0~1 之间)。freq f指定 f 变量为频数变量。 SAS 程序运行结果: 以上是通过 class 语句对因素 a 和因素 b 自动赋哑变量的结果。可以看到,两因素均以最后一个水平为基准。以 a 因素为例,哑变量 a1 表示 a 因素的第一个水平相对于第三个水平进行分析;哑变量 a2 表示 a 因素的第二个水平相对于第三个水平进行分析。b 因素的哑变量意义类似。 Summary of stepwise selection 以上为逐步筛选法的筛选结果,最终只有因素 b 进入了回归方程(χ2= 13.4863,P= 0.0037)。 Score test for the proportional odds assumption 以上为平行线假设的检验结果:χ2= 0.8909,P= 0.8276> 0.05,说明资料满足平行线假设。 Type 3 analysis of effects 以上是将因素 b 作为一个整体的假设检验结果:waldχ2= 13.5102,P= 0.0037 < 0.05,说明病程对疗效的影响有统计学意义。 Analysis of maximum likelihood estimates 以上为参数估计及假设检验的结果。本例结果变量有 3个水平,故模型包含 2 个截距项。若P1、P2和P3分别表示治愈、好转和无效发生的概率,则回归方程为: Odds ratio estimates 以上是对优势比的估计结果:OR1vs4= 2.576,其 95%置信区间为(1.445,4.592);OR2vs4= 2.473,其 95%置信区间为(1.205,5.072);OR3vs4= 1.382,其 95%置信区间为(0.830,2.302)。 统计及专业结论:病程对疗效的影响有统计学意义(P= 0.0037 < 0.05),而试验中心对疗效的影响没有统计学意义。OR1vs4= 2.576,其 95%置信区间为(1.445,4.592),说明病程小于 1 个月的疗效是病程大于 5年疗效的2.576倍;OR2vs4= 2.473,其 95%置信区间为(1.205,5.072),说明病程为1~3 个月的疗效是病程大于 5年疗效的 2.473 倍;OR3vs4= 1.382,其 95%置信区间为(0.830,2.302),说明病程为3 个月~5年的疗效是病程大于 5年疗效的 1.382 倍。 [1]Hu LP.Statistics facing practical scientific issues -- (2) multi-factor designs and linear model analysis.Beijing: People’s Medical Publishing House, 2012:508-517.(in Chinese)胡良平.面向问题的统计学——(2)多因素设计与线性模型分析.北京: 人民卫生出版社, 2012:508-517. [2]Hu LP.Medical statistics-analysis of quantitative and qualitative data applying the triple-type theory.Beijing: People’s Military Medical Press, 2009:363-375.(in Chinese)胡良平.医学统计学-运用三型理论分析定量与定性资料.北京:人民军医出版社, 2009:363-375.
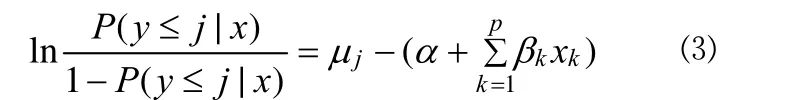
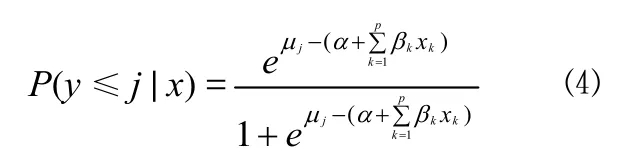


2 变量赋值