基于稀疏表示的二值图像超分辨率重建算法
2017-12-20沈怡灵赵明哲李强懿李博涵
沈怡灵,赵明哲,李强懿,李博涵,2,3
(1.南京航空航天大学 计算机科学与技术学院,江苏 南京 210016;2.软件新技术与产业化协同创新中心,江苏 南京 210093;3.江苏易图地理信息科技股份有限公司,江苏 扬州 225009)
基于稀疏表示的二值图像超分辨率重建算法
沈怡灵1,赵明哲1,李强懿1,李博涵1,2,3
(1.南京航空航天大学 计算机科学与技术学院,江苏 南京 210016;2.软件新技术与产业化协同创新中心,江苏 南京 210093;3.江苏易图地理信息科技股份有限公司,江苏 扬州 225009)
目前,关于二值图像的超分辨率重建的研究很少,而二值图像应用广泛,低分辨率的二值图像会导致对其识别困难。针对这一现状,对基于稀疏表示的二值图像的超分辨率重建进行深入研究,提出了一种针对二值图像的超分辨率重建算法。一方面,分析二值图像具有的明显特征,对其进行针对性的边缘特征及纹理特征的提取,以更精确地表示二值图像的高频信息,提供更多的先验信息,提高二值图像的重建质量。另一方面,针对二值图像中存在二维码图像、文本图像等不同类型的图像这一特点,将聚类算法融合到字典学习中,使得学习得来的字典更适用于不同类型的二值图像。实验结果表明,提出的针对二值图像的基于稀疏表示的超分辨率重建算法对二值图像有很好的重建效果,对噪声具有一定的鲁棒性。
二值图像;稀疏表示;超分辨率重建;特征提取;字典学习
0 引 言
图像的超分辨率重建技术[1]就是要突破成像设备自身的分辨率的限制,通过输入的一张或者多张低分辨率图像,根据一些假设或者先验知识等,通过算法重建出其对应的高分辨率图像,以期重建的图像能恢复出更多的细节信息,跟原始的高分辨率图像差距更小。该技术已广泛应用于各个领域。
二值图像作为图像中一种重要的类型,在实际应用中频繁出现,例如二维码图像、条形码图像、文本图像等,是二值图像的典型代表。各类条码在如今的生活中越来越普及,人们的生活已经离不开手机扫码这一方便快捷的方式,文本也是一类重要的信息获取来源,都有着广泛的应用场景。而低分辨率的二值图像会对其识别产生很大影响,因此,对二值图像进行超分辨率重建具有其重要意义。
近年来,学者们针对图像的超分辨率重建这一问题提出了许多算法[2-4]。Yang等[5-6]提出了一种新的图像超分辨率重建方法,采用稀疏表示理论,引领了图像超分辨率重建算法的新潮流。自Yang的算法提出后,出现了很多基于稀疏表示的方法。Zeyde等[7]先单独训练低分辨率字典,再根据稀疏表示推导出高分辨率字典,加快了重建的速度。Zhang等[8]提出了一种基于快速学习的超分辨率重建算法,通过学习双字典,采用简单的矩阵乘法代替稀疏重建步骤,使得计算更有效率。Dong等[9]引入稀疏编码噪声的概念,将目标转为抑制噪声,提出了非局部集中稀疏表示(NCSR)模型。Liu等[10]提出了一种基于不同形态学正则化的稀疏表示算法。Peleg等[11]为了避免不变性假设,采用基于稀疏表示的统计预测模型。Zhang等[12]提出一个基于结构调整的稀疏表示的联合超分辨率框架以改善重建效果。不过,以上基于稀疏表示的超分辨率重建算法都不是针对二值图像,目前对于二值图像的有针对性的研究较少,但是对二值图像的超分辨率重建研究很有必要。
因此,针对这一现状,对基于稀疏表示的二值图像超分辨率重建进行研究。需要指出的是,文中的二值图像是广义上的二值,指的是输入的低分辨率图像的像素灰度值集中分布在两个区间段内的图像,而非传统意义上的灰度值只有0和1两种取值的二值图像。
1 基于稀疏表示的二值图像超分辨率重建
1.1 稀疏表示理论
稀疏表示的基本思想[13]是自然信号可以通过预定义的原子来线性表示。设信号x∈Rn,可得:
(1)
其中,D∈Rn×L(n≪L),D=[d1,d2,…,dL];di(i=1,2,…,L)为矩阵D的原子;α=[α1,α2,…,αL]T∈RL为稀疏表示向量。
稀疏表示问题就是要找出信号x最稀疏的表示,也就是α中的非零点最少的情况。因此,该问题可表述为:
min‖α‖0s.t.x=Dα
(2)
其中,‖·‖0计算L0范数,即α中非零元素的个数,α为x的稀疏表示,也称为稀疏表示系数;D为稀疏变换矩阵,也就是稀疏字典。
然而求解式(2)是个NP难问题,在足够稀疏的条件下,L0范数和L1范数的优化问题存在相同解[14],因此,式(2)可转换为:
min‖α‖1s.t.x=Dα
(3)
其中,‖·‖1计算L1范数,其结果为向量中所有元素的绝对值之和。考虑到实际中的噪声问题,式(3)可转化为:
(4)
其中,ε为噪声或稀疏表示误差。
式(4)也可以转换为如下的正则化方式:
(5)
其中,μ为正则化参数,用以平衡稀疏表示误差和稀疏性。
因此,稀疏表示问题就是当已知字典D时,求解信号x的最稀疏的系数α,这可以通过最大后验概率估计、匹配追踪、基追踪、基于稀疏贝叶斯等算法来求解。
1.2 二值图像超分辨率重建模型
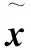
(6)
其中,DL为低分辨率二值图像特征块的字典,通过对大量的二值图像训练样本学习得到。
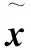
y=DHα*
(7)
其中,DH为高分辨率二值图像的字典。
在得到每一个高分辨率二值图像块后,按照对应位置进行合成,就可以得到对应的高分辨率二值图像。
2 二值图像特征提取
由于人眼对图像的高频信息较为敏感,低分辨率图像的高频信息对重建高分辨率图像的高频细节很重要,提取图像特征块是为了提取出图像中较为重要的高频部分,使得计算出的稀疏系数可以更好地对高分辨率图像块进行重建。二值图像主要包括二维码图像、条形码图像和文本图像等,这些图像都有清晰的边缘特征和明显的纹理特征。因此,文中主要通过这两方面来对二值图像特征进行提取。
2.1 边缘特征
由于Kirsch算子[15]可以提供较为全面的边缘信息,对边缘的提取比较精准,具有很好的边缘检测效果,文中采用该算子来提取二值图像的边缘信息。
Kirsch算子采用8个方向的差分模板依次对图像的3×3邻域进行对应的8个方向的检测,这8个方向中响应的最大值即为该邻域中心像素点上的边缘强度,相应的最大值的方向即为该像素的边缘方向。
将Kirsch算子的8个模板作用于图像块上的结果分别记为K0,K1,…,K7,则该邻域中心位置(x,y)处的边缘强度为:
K(x,y)=max{Ki}(i=0,1,…,7)
(8)
通过式(8),即可提取二值图像中每一点的边缘信息。
2.2 纹理特征
局部二值模式(LBP)[16]可以很好地刻画图像的局部纹理特征,并通过不同邻域位置点的不同权重将邻域像素的空间位置关系考虑在内。另外,LBP算子考虑3×3的图像区域,针对图像块提取纹理特征,这与文中研究的需求一致。该算子还有鲁棒性好、对光照变化不敏感等优点。所以,采用LBP算子提取二值图像的纹理特征。
LBP算子描述的是图像的局部纹理信息,用该算子进行特征提取的具体步骤为:
(1)设定窗口大小。通常LBP算子采用的窗口大小为3×3,也就是考虑一个像素的8邻域;
(2)邻域像素二值化。以窗口的中心点像素灰度值为阈值,比较该像素的8个邻域像素与阈值的大小,像素值大于阈值的邻域点标记为1,反之标记为0。如此,经比较就可以得到8个值为0或1的标记值;
(3)求解LBP值。对第2步中得到的8位标记值进行加权求和,即可得到这一窗口的LBP值。上文所述的对8位标记值进行加权求和可以理解为将8位标记值组成的二进制数转化为十进制数。
上述LBP值的计算可归纳为如下数学形式:
(9)
其中,(xc,yc)为窗口中心点的坐标;gc为中心点像素的灰度值;P为窗口内除中心点外其余点的个数,对于大小设定为3×3的窗口,P的值为8;gi(i=0,1,…,P-1)为中心点各个邻域的灰度值。式(9)的结果即为点(xc,yc)处的LBP值。
对图像中的每一个像素点,通过式(9)求出LBP值,就可以得到基于LBP算子的图像纹理特征。
2.3 特征提取
除了上述的边缘特征和纹理特征之外,还使用了水平和垂直两个二阶梯度算子,以进一步对低分辨率二值图像的特征进行有效提取。这两个二阶梯度算子分别定义如下:
H1=[-1,0,2,0,-1]
(10)
H2=[-1,0,2,0,-1]T
(11)
通过Kirsch边缘检测算子、LBP算子及以上两个二阶梯度算子提取的二值图像特征可以表示为:
(12)
3 基于聚类的字典学习方法
3.1 联合字典学习
由1.2节可知,在重建高分辨率二值图像时,用了低分辨率二值图像特征块的稀疏表示系数α*。因此,要保证高、低分辨率二值图像在通过高分辨率字典DH和低分辨率字典DL稀疏表示时的稀疏系数相同,可以通过对高、低分辨率图像(特征)块的联合字典学习来实现。
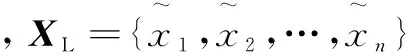
(13)
(14)
其中,A为XL和YH的稀疏表示系数矩阵;DL和DH分别为对应XL和YH的稀疏字典;μ为正则化参数。
然后,合并式(13)和式(14)可得:
(15)
其中,M和N分别为向量形式下高、低分辨率图像(特征)块的维数。
这样,就将高、低分辨率字典统一到同一个稀疏编码框架中,以保证稀疏表示系数的相同。式(15)可由K-SVD算法[17]求解。
3.2 基于聚类的字典学习
由于二值图像训练样本中包含了二维码图像、条形码图像、文本图像等不同类型的二值图像,这些图像的特征不尽相同,甚至对于同一种类型的图像也有些许不同。比如不同模块宽度的二维码图像之间就有差异。如果用同一个字典来表达这些不同类型的二值图像是不够准确的,若对不同类型的图像采用不同的字典,对重建二值图像有积极作用。因此,为了让稀疏字典更加合理、更有针对性,首先通过聚类算法将训练样本中的二值图像块聚成K类,再对每一类中的样本图像块分别进行对应的聚类子字典的学习,由此产生针对K类二值图像块的K对高、低分辨率字典,用于二值图像的超分辨率重建,以进一步提高二值图像重建的质量。
K-means聚类算法具有复杂度低、处理数据效率高、算法收敛较快等显著优点,可以用于处理较大的数据集。因此,文中采用该算法来对训练样本集中的二值图像块进行聚类。K-means聚类算法的基本思想是:首先随机选取K个样本来初始化聚类中心,随后对样本中的每一个数据,依次判断其属于哪一类,然后更新聚类中心,如此不断迭代直至收敛。
基于K-means聚类的字典学习方法的步骤如下:
(1)选取合适的二值图像,作为字典学习的训练样本,将这些二值图像分成5×5大小的图像块;
(2)确定字典学习所需的图像样本块数量,随机选取该数量的高、低分辨率二值图像样本块对;
(3)对图像块样本集进行K-means聚类,得到K个样本子集;
(4)对每一个样本子集,通过K-SVD算法进行高、低分辨率字典的学习,得到K对高、低分辨率字典。
基于该字典学习方法的二值图像超分辨率重建的过程如下:
(1)将输入的低分辨率二值图像进行特征提取,得到低分辨率图像特征块;
(2)对每一个低分辨率二值图像特征块:
求解其在K个低分辨率子字典下的稀疏表示系数,以及到这K个聚类中心的距离;
通过该系数和对应的高分辨率子字典,求解出对应的K个高分辨率二值图像块;
将这K个高分辨率二值图像块加权合成一个高分辨率二值图像块,该结果即为重建出的对应输入的低分辨率二值图像特征块的高分辨率二值图像块。其中,权重系数即为步骤(1)中所求得的低分辨率二值图像特征块到各个聚类中心的距离的倒数。
(3)在循环完所有的低分辨率二值图像块,得到所有的对应的高分辨率二值图像块后,将其合成高分辨率二值图像。
4 仿真实验分析
为了验证对二值图像超分辨率重建的有效性,选择Bicubic、Yang[6]和BP[18]三种算法对二值图像超分辨率重建效果进行对比。文中算法在实验中的参数设置如下:稀疏字典的大小为256,训练样本块数量为10 000,聚类个数为3,正则化参数为0.15,图像的放大倍数为2,即对输入的低分辨率二值图像的长宽都放大2倍,重建出其对应的高分辨率二值图像。
在实验中,随机选取了9张二值图像作为实验数据,并标记为图像0到图像8。其中,图像0~2为二维码图像,图像3~5为条形码图像,图像6~8为文本图像,选择这几种典型的二值图像类型以验证文中算法对二值图像重建的效果。采取指标峰值信噪比(PSNR)来评价算法对二值图像的重建质量。PSNR值越高,说明重建出的高分辨率图像和原始的高分辨率图像越接近,重建质量越好。
实验结果如表1所示。由于对训练样本块的选取是随机的,所以对每一张二值图像,都进行了10次实验,取10次结果的平均值,得来的结果更具代表性和准确性。
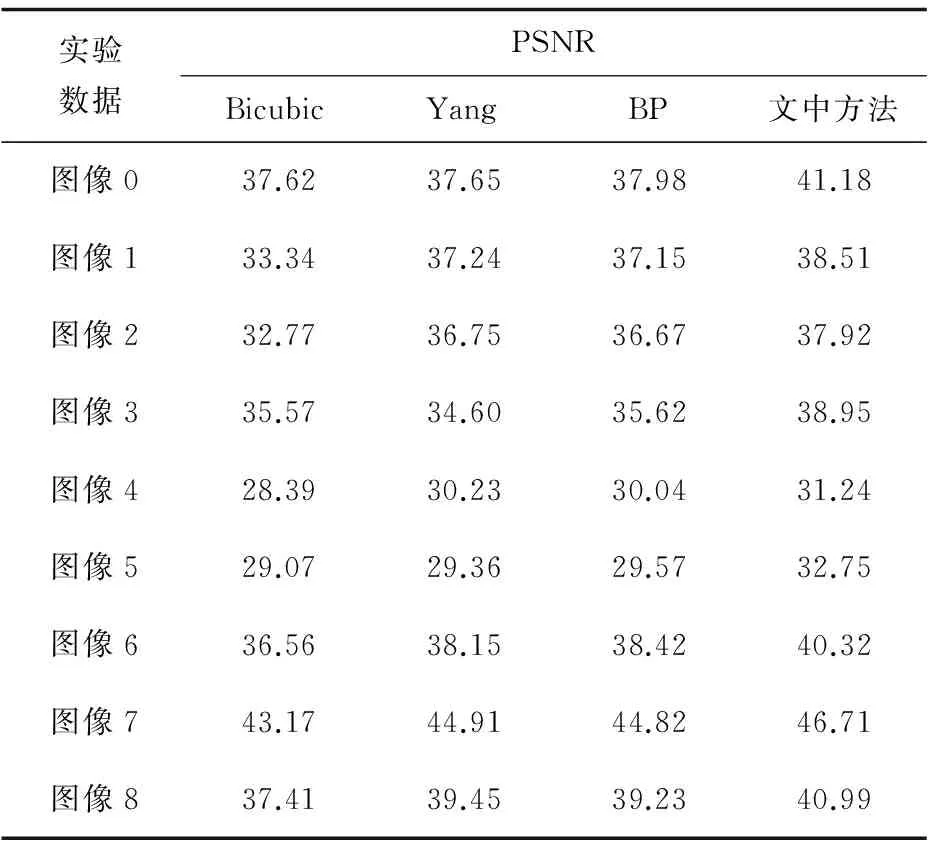
表1 不同算法对二值图像重建效果对比
从表1可知,文中算法在各类二值图像上均取得了更好的效果,说明了该算法对二值图像的超分辨率重建有着很强的针对性,重建质量较好。
图1展示了不同算法对同一幅文本图像的超分辨率重建效果。
从图1可以看出,Bicubic方法的结果较为模糊,Yang算法和BP算法结果相近,明显优于Bicubic,而文中算法对二值图像的细节信息重建的更加完整,优于其他算法,有更好的视觉效果。

图1 结果对比
由于在实际情况中,图像不可避免地会受到噪声的影响,因此,算法对噪声的鲁棒性也是值得考虑的一个方面。选取二维码图像0,条形码图像3,文本图像6进行本次实验,对输入的低分辨率二值图像施加均值为0,标准差为0~10的高斯噪声,对这些不同程度的含噪二值图像进行超分辨率重建,结果如表2所示。
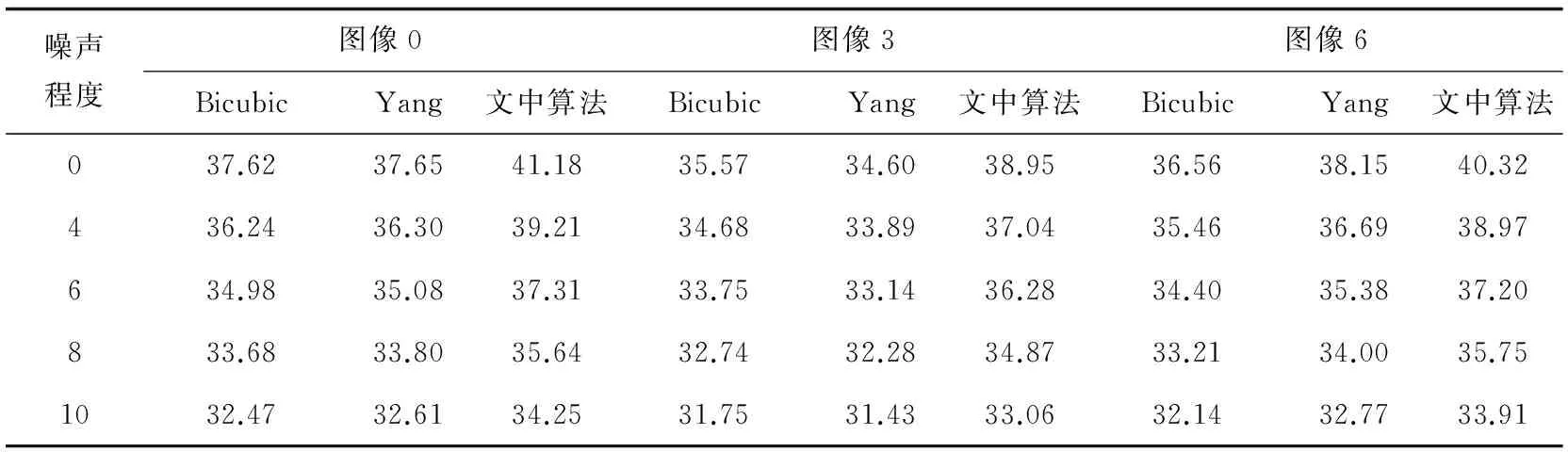
表2 重建含噪二值图像效果对比
从实验结果可知,随着高斯噪声程度的不断增强,Bicubic算法、Yang算法以及文中算法都有在一定程度(可接受)的下降,不过,都保持着较好的重建效果。对比其他方法,文中算法均保持着更高的PSNR值。PSNR指标值的下降幅度不大,说明文中算法在抗噪声这一方面的优势,对噪声具有鲁棒性。
5 结束语
提出了一种针对二值图像的基于稀疏表示的超分辨率重建算法。通过提取二值图像的边缘特征和纹理特征,可以有效地重建二值图像的高频细节。另外,二值图像中存在二维码图像、文本图像等不同类型的图像,针对这一特点,提出了适用于二值图像的字典学习方法,进一步提高了二值图像重建的效果。在对含噪二值图像的重建上,该算法表现出了不错的效果。但是仍存在不足之处,在提高二值图像重建速度这一方面,还需进一步的研究与探索。
[1] Ren C,He X,Teng Q,et al.Single image super-resolution using local geometric duality and non-local similarity[J].IEEE Transactions on Image Processing,2016,25(5):2168-2183.
[2] Li X,Lu X,Yuan H,et al.Geometry constrained sparse coding for single image super-resolution[C]//IEEE conference on computer vision and pattern recognition.[s.l.]:IEEE,2012:1648-1655.
[3] Dong W,Zhang D,Shi G.Centralized sparse representation for image restoration[C]//International conference on computer vision.[s.l.]:IEEE,2013.
[4] Zhang J,Zhao C,Xiong R,et al.Image super-resolution via dual-dictionary learning and sparse representation[C]//IEEE international symposium on circuits and systems.[s.l.]:IEEE,2012:1688-1691.
[5] Yang J,Wright J,Huang T,et al.Image super-resolution as sparse representation of raw image patches[C]//IEEE conference on computer vision and pattern recognition.[s.l.]:IEEE,2008:1-8.
[6] Yang J,Wright J,Huang T S,et al.Image super-resolution via sparse representation[J].IEEE Transactions on Image Processing,2010,19(11):2861-2873.
[7] Zeyde R,Elad M,Protter M.On single image scale-up using sparse-representations[C]//International conference on curves and surfaces.[s.l.]:[s.n.],2010:711-730.
[8] Zhang H,Zhang Y,Huang T S.Efficient sparse representationbased image super resolution via dual dictionary learning[C]//IEEE international conference on multimedia and expo.[s.l.]:IEEE,2011:1-6.
[9] Dong W,Zhang L,Shi G,et al.Nonlocally centralized sparse representation for image restoration[J].IEEE Transactions on Image Processing,2013,22(4):1620-1630.
[10] Liu W,Li S.Sparse representation with morphologic regularizations for single image super-resolution[J].Signal Processing,2014,98(5):410-422.
[11] Peleg T,Elad M.A statistical prediction model based on sparse representations for single image super-resolution[J].IEEE Transactions on Image Processing,2014,23(6):2569-2582.
[12] Zhang Y,Liu J,Yang W,et al.Image super-resolution based on structure-modulated sparse representation[J].IEEE Transactions on Image Processing,2015,24(9):2797-2810.
[13] Mairal J,Elad M,Sapiro G.Sparse representation for color image restoration[J].IEEE Transactions on Image Processing,2008,17(1):53-69.
[14] Candes E J,Tao T.Near-optimal signal recovery from random projections:universal encoding strategies?[J].IEEE Transactions on Information Theory,2006,52(12):5406-5425.
[15] Acharya T,Ray A K.Image processing: principles and applications[M].[s.l.]:John Wiley & Sons,2005.
[16] Ojala T,Pietikainen M,Maenpaa T.Multiresolution gray-scale and rotation invariant texture classification with local binary patterns[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(7):971-987.
[17] Aharon M,Elad M,Bruckstein A.K-SVD:an algorithm for designing overcomplete dictionaries for sparse representation[J].IEEE Transactions on Signal Processing,2006,54(11):4311-4322.
[18] Polatkan G,Zhou M,Carin L,et al.A Bayesian nonparametric approach to image super-resolution[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2015,37(2):346-358.
ASuper-resolutionReconstructionAlgorithmforBinaryImageBasedonSparseRepresentation
SHEN Yi-ling1,ZHAO Ming-zhe1,LI Qiang-yi1,LI Bo-han1,2,3
(1.School of Computer Science and Technology,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China;2.Collaborative Innovation Center of Novel Software Technology and Industrialization,Nanjing 210093,China;3.Jiangsu E-Map Geographic Information Technology Co.,Ltd,Yangzhou 225009,China)
At present,there is little research on binary image super-resolution reconstruction.Binary image is widely used,but that of low-resolution will result in identification difficulties.In view of this,with deep research on binary image super-resolution reconstruction based on sparse representation,a super-resolution reconstruction algorithm for binary image is proposed.On the one hand,obvious features of the binary image are analyzed,and the edge and texture features of that are extracted to represent its high frequency information more accurately.Therefore,more priori information is provided,and the reconstructed quality of binary image is improved.On the other hand,for the different types in binary images,such as two-dimensional bar code and text,the clustering algorithm is integrated into dictionary learning,so that the learned dictionaries are more suitable for different types of binary image.Experimental results show that the proposed algorithm has a good effect in reconstruction for the binary image,with a certain robustness against noise.
binary image;sparse representation;super-resolution reconstruction;feature extraction;dictionary learning
TP301.6
A
1673-629X(2017)12-0043-05
10.3969/j.issn.1673-629X.2017.12.010
2016-12-28
2017-04-28 < class="emphasis_bold">网络出版时间
时间:2017-08-01
国家自然科学基金资助项目(61375021);国家自然科学基金青年基金(41301407)
沈怡灵(1992-),女,硕士研究生,研究方向为数字图像处理和模式识别。
http://kns.cnki.net/kcms/detail/61.1450.TP.20170801.1556.070.html
