用“数形结合”解决“根的个数”的两个注意点
2013-05-12费劲男
费劲男
(江苏省南通市平潮高级中学,南通 226311)
“数形结合”是一种基本的数学方法,也是贯穿整个高中阶段的一种重要的思想方法,它兼有数的严谨与形的直观,利用它可使复杂问题变得简单、抽象问题变得具体,是优化解题过程的重要方法之一。数形结合的思想,其实质就是将抽象的数学语言与直观的图形结合起来,在代数与几何图形之间进行相互转化,从而拓宽解题思路,提高解题速度与质量。熟练运用数形结合来解题,可起到事半功倍的效果。
“方程根的个数”是高三复习的一个重要题型,也是函数与方程的一个重要应用,一般出现在填空题的后几题或是解答题中。在解决这类问题时,通常采用将方程的解转化为两个函数图像的交点,再利用数形结合直观的找到结果。整个的解题过程中,图象是最关键的一部分,画图是否准确,有没有忽视考虑图形的整体性,如等价性原则等,都会导致图象出错。如何作出正确的函数图象,要注意以下两个问题:
一、正确确定变量的取值范围
“数缺形,少直观;形缺数,难入微”。数形结合就是利用函数和函数图象来解决问题的一种思想方法,对于“根的个数”是方程问题,所以要解决这类问题首先要将方程转化为函数,这过程就要注意等价性原则,在不改变原先变量范围的基础上进行等价变形。
例 1、若方程 l g(x-1)+l g(3-x)=l g(a-x)只有一个根,则 α的取值范围是__ 。分析:本题是对数方程求解问题,需将对数方程转化为一元二次方程,此时就要先确定的范围,再将其变形,转化为函数。
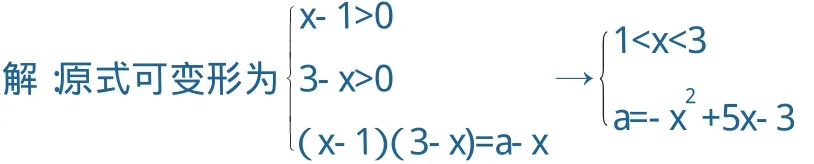

即转化为函数y=a与函数y=-x2+5 x-3 x∈(1,3)的图象只有一个交点,如图所示,在同一坐标系内作出两个函数图象,要使两个函数图象只有一个公共点,则α的取值范围是(1,3]∪}。
点评:所有的等式变形转化问题,都要先考虑变量的范围,再进行等价变形,在有范围约束的条件下,做出正确的函数图象,同时注意图象的端点。
例2、事实证明:总存在正实数a,b(a 分析:本题是指数的形式,需等式两边同取对数,将指数下移,再转换成函数,利用数形结合来解决。 点评:本题利用构造函数的方法转化为两函数图象问题,容易出错的地方:1.不考虑x>e时,函数值0 有些函数的定义域是一个区间中去掉一个或几个值,那么这些值体现在图象中很可能就是它的渐近线,比如函数y=,定义域为(-∞,0)∪(1,+∞),直线x=0就是它的一条渐近线。再比如函数y=1 n│x-1│定义域为(-∞,0)∪(1,+∞),直线x=1是渐近线。也有些函数是由一些图像本身就有渐近线的基本函数,如y=ex,y=1 n x等,通过平移、翻折等变换得到的,那么,这些函数也就有渐近线。 分析:本题中提到解的个数,很显然利用图像最直观。 在同一坐标系内作出两个函数图象, 有图可知,当0≤a 点评:本题的关键是在等价变形的过程中,1 n x≠0,即x≠1,函数图象不可能与直线x=1有交点,所以x=1只能是它的一条渐近线。 分析:本题将方程转化后得到含绝对值的函数,关键是如何作出其图像。 点评:本题的渐近线是由函数y=2x经过平移、翻折之后保留下来的。 本文的四个例题都采用了数形结合的思想,很直观的找到所需要的结果。文中提到的两个注意点是本人在数形结合的教学中学生错误率较高的两个问题,当然还存在着其他的一些,比如由方程的解转化为哪两个函数图象的交点,有参数的是否一定要分离之后才进行数形结合,等等。其实,最关键的是让学生知道在什么情况下使用数形结合的方法,以及如何作出正确的函数图像。 从例题中不难发现,运用数形结合思想,不仅直观、容易发现解题途径,而且能避免复杂的计算与推理,大大简化了解题过程,特别是在解填空题时更能体现出其优越性。高中数学教学过程中,许多抽象性的问题学生往往觉得难以理解,不知该如何去应用解决,遇到问题,望而却步,如果教师能及时灵活地引导学生进行数形结合,转化为直观易懂的问题,学生就容易理解,进而解决问题并获得成功的体验。学生如果运用数形结合思想解决了一些有难度的问题,这对于提高学生学习数学的积极性并增强其学好数学的信心有很大的帮助。
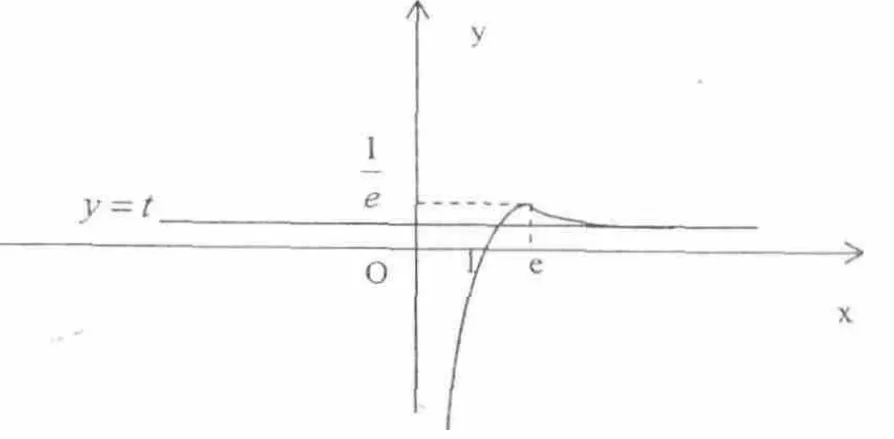
二、注意渐近线的应用



