融合边缘信息的极值中值滤波算法

金秋春，童小利，薄树奎

(1.郑州航空工业管理学院计算机系，河南郑州450015;2.郑州航空工业管理学院机电工程学院，河南郑州450015)

数字图像处理技术已广泛应用于各个领域，如医学、工业检测、航天等，但数字图像在采集、传输、存储和处理过程中，不可避免地引入了各种噪声。噪声恶化了图像的质量，给接下来的图像处理工作，如边缘检测、图像分割、特征识别等带来很大困难。因此，有效地清除噪声是图像处理的重要环节，一直是图像预处理的热点研究主题。

图像去噪的主要方法是进行图像滤波，理想的滤波算法是只对噪声点进行处理，而保留信号灰度值不变。TUKEY 在 1971年提出的中值滤波算法(SM)[1]，利用邻域中值代替图像像素灰度值，是非线性滤波的典型代表，被广泛应用于消除图像中的脉冲噪声。但标准的中值滤波存在固有缺陷:由于对所有数据采用统一的处理方法，因此，不仅改变了噪声点的值，也改变了信号点的值，并使噪声在邻域中传播。为了改进标准中值滤波算法的不足，近年来出现了多种基于中值滤波的改进型算法。BROWNRIGG 提出了加权中值滤波算法[2]，通过加权，降低了细节的损失，但其去噪性能也同时下降了。SUN 等提出了开关中值滤波算法[3]，但只有在图像噪声密度很小的条件下才能取得良好的去噪效果。刑藏菊等提出了极值中值滤波(EM)算法[4]，该方法操作简单，但对检测出的噪声采用的是标准中值滤波方法，在图像噪声密度较大时性能大大下降。

文中提出的融合边缘信息的极值中值滤波算法，主要是利用边缘像素与噪声像素显著差异正确地检测出噪声点，避免了图像边缘像素被误判为噪声而被中值替代，造成图像细节信息的损失。同时，在噪声点恢复时采用邻域内非噪声像素值的中值，恢复值更加接近真实值。

1 融合方向信息的噪声检测

极值滤波思想是当像素I(x，y)是在以(x，y)为中心、大小为N×N 邻域的极值时，则认为该像素是噪声。该方法在检测出噪声的同时，误将部分边缘点当作噪声。通过观察发现，噪声点与邻域内任意方向上其他像素之间均存在较大跃变，而边缘点在某一方向上与该方向上其他像素之间跃变较小。因此，文中提出融合方向信息的噪声检测方法，具体如下:

(1)取图像I 中以(x，y)为中心、大小为n×n邻域像素(记为NB(x，y))，无重复升序排序后存放在向量V中，长度为L(L ≤n×n);

(2)如果I(x，y)==V(1)或者I(x，y)==V(L)，即该像素是该邻域的极值，疑似为噪声，则转入第(3)步;否则转入第(8)步;

(3)将疑似噪声点邻域NB(x，y)内像素与8个相同大小的方向模板DBk(k=1，2，…，8)对应位置元素进行点乘运算，保留非0值，即为各个方向上的像素集合Pk(k=1，2，…，8)。文中邻域大小n=7，8个方向的方向模板如图1所示。

图1 7×7方向模板

(4)为了消除疑似噪声像素的影响，排除各个方向上等于I(x，y)的元素，集合记为，求集合的中值mk(近似为该方向均值):

(5)计算疑似噪声像素I(x，y)与各个方向其他像素中值mk差的绝对值cmk:

(6)求出{cm1，cm2，…，cm8}最小值所对应的方向d 并计算出该方向上的方差sd:

(7)如果cmd＞thresh，即该像素与该方向上其他像素之间均有较大跃变，同其他方向上的像素之间则有更大跃变，则认为该像素是噪声，标记为flag(x，y)=1;否则认为该像素是边缘点，标记为flag(x，y)=0。

这里阈值thresh 采用动态阈值，依据当cmd＞3sd时认为是小概率事件，判断为噪声点，设置为:

(8)该像素标记为flag(x，y)=0，对图像中的下一个像素转入第 (1)步，直到所有像素进行完毕，可以得到噪声标记图flag。

2 开关中值滤波

传统中值滤波是对所有像素I(x，y)用该邻域的中值替换，因此，在消除噪声的同时，也改变了非噪声点的值，特别是造成了边缘细节信息的损失。文中只对噪声点进行中值滤波，而且根据噪声点标记图flag，使用邻域中非噪声点像素的中值滤波，这对噪声污染严重的图像滤波效果尤为明显，具体流程如下:

(1)对图像中位置为(x，y)的像素，如果flag(x，y)=1，则从图像I 和噪声标记图flag 中分别取以(x，y)为中心、大小为n×n的邻域，记为WI(N)和Wf(N)，转入第 (2)步;否则，转入第(4)步;

(2)求该像素邻域WI(N)中未受噪声污染的像素集合方法为:

其中:“·”为对应元素点乘运算，1－Wf(n)中值为1的元素是该邻域中未受噪声污染像素的对应位置。

去掉WIS(N)中0值，剩下非0值集合~WIS即为该邻域未受噪声污染的像素集合。

(3)求该邻域未受噪声污染像素~WIS的中值m(x，y)，对该噪声点进行滤波:

(4)对图像中的下一个像素转入第(1)步，直到所有像素进行完毕。

3 实验结果分析

为了验证该算法的滤波性能，进行了大量的实验，以下是其中的部分实验结果。首先以“Lena”图像为例，分别使用7×7中值滤波、7×7极值滤波和文中滤波方法进行对比实验。在每次实验中，不同密度的椒盐噪声随机地加到原始图像上，以输出图像的信噪比为评价标准，比较滤波器的性能。设I(x，y)表示未加噪声的原始图像，N(x，y)表示加噪图像，O(x，y)表示加噪滤波后输出图像，则输出图像信噪比SNR[4]为:

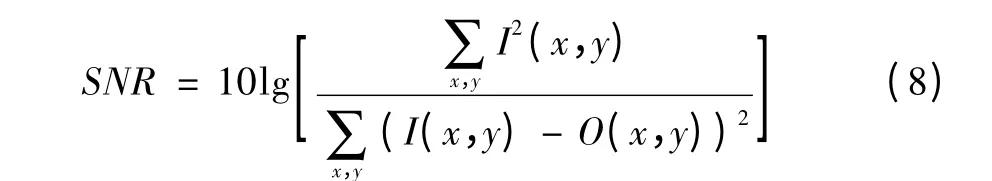
图2显示的是分别对原始Lena 图像加入不同密度的椒盐噪声经过7×7中值滤波、7×7极值滤波和文中方法滤波后的图像信噪比 (单位:dB)。可以直观地看出:文中方法在各种输入噪声密度下，滤波效果都较好，特别是噪声密度比较大时 (D ＞ 0.5)，该方法明显优于中值滤波和极值滤波方法，这是由于文中提出的方法能准确识别出噪声。

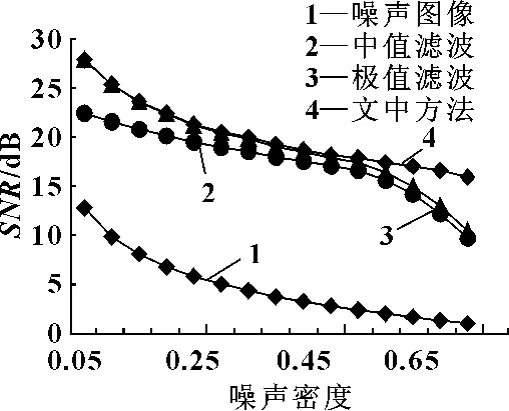
图2 各滤波器输出图像信噪比与噪声密度的关系

在衡量滤波器去噪效果的同时，还要考虑对图像细节的保护能力，通常将滤波后图像与无噪声图像之间的相似度作为滤波算法适应度评估函数。这里采用下面2种常用评价准则来衡量滤波后图像与无噪声图像之间的相似度[5－6]:

其中:K1、K2分别表示图像第一维、第二维大小。

使用Lena、Peppers 和Baboon 图像作为测试图像，加入噪声密度为D=0.6的噪声，采用MAE、MSE 误差来度量滤波算法的边缘和细节保护能力，同时采用信噪比SNR 来衡量其滤除噪声的程度。从表1可以看出:在所有测试图像中，文中方法在保持最小滤波误差的同时，具有最大的输出信噪比。

表1 各种滤波器对不同图像滤波效果比较

4 结束语

文中提出的融合边缘信息的极值中值滤波算法，主要是在噪声点的检测上利用边缘像素相关性的特点，减少了图像细节部分被误判噪声的错误率，同时对噪声点使用邻域内未受噪声污染的像素中值进行恢复，恢复值更加接近真实值，因此，该算法具有良好的滤波性能。

【1】TUKEY J W.Exploratory Data Analysis[M].Addison-Wesley，1971.

【2】BROWNRIGG D R K.The Weighted Median Filter[J].Communications of the ACM，1984，27(8):807－818.

【3】SUN T，NEUVO Y.Detail-preserving Median Based Filters in Image Processing[J].Pattern Recognition Letters，1994，15(4):341－347.

【4】刑藏菊，王守觉，邓浩江，等.一种基于极值中值的滤波算法[J].中国图像图形学报，2001，6(6):533－536.

【5】LUKAC R，SMOLKA B，PTATANIOTIS K N，et a1.Color Image Denoising Usin Evolutionary Computation[J].International Journal of Imaging Systems and Technology，2006，15(5):236－251.

【6】李秀玲，何劲松.基于旋转不变像素相关性的加权中值滤波器[J].中国图像图形学报，2010，15 (1):56－62.