基于径向基函数代理模型的板料成形回弹预测

杨川，谢延敏，隆强

(西南交通大学，四川成都610031)

代理模型作为分析工具和优化算法之间的接口，得到了广泛的应用和发展。所谓代理模型，是指在不降低精度的情况下构造的一个计算量小、周期短，但计算结果与数值分析或物理实验结果相近的数学模型[1]。它是利用已知点(样本)的响应信息来预测未知点响应值的一类模型，其实质是以拟合精度和预测精度为约束，利用近似方法对离散数据进行逼近的数学模型。代理模型的构造在数学上可以通过拟合和插值来实现，具体方法有多项式拟合、插值和级数拟合等经典方法，也有径向基函数插值与Kriging 插值等新方法。其中，径向基函数插值被证明是一种高精度的代理模型构造方法[2－3]。

作者提出了基于径向基函数(RBF)的代理模型方法，并结合U形薄板零件的冲压成形参数进行正交试验方案设计，利用径向基函数建立代理模型[4－5]。U形件是一种具有代表性的冲压成形件。对此类零件的成形技术和冲压成形过程中回弹的研究，对其他更复杂车身覆盖件冲压成形和冲压模具开发，有一定的借鉴与参考价值。

1 利用Dynaform 进行成形模拟及回弹分析

以国际著名的数值模拟会议NUMISHEET’93的U形件成形为例，模具结构如图1所示，应用Dynaform 对U形件的成形及回弹进行模拟[6]。

图1 模具结构图

板料采用铝合金板材，长度为350 mm，宽度为35 mm，厚度为1 mm，拉延深度为70 mm。

材料应力应变关系见下式:

σ=K(ε0+ε)n

式中:σ为应力;

K为材料常数;

ε0为初始应变;

ε为塑性应变;

n为加工硬化系数。

材料参数如表1所示。

表1 材料参数

1.1 模型验证

(1)利用UG 对U形件的凸凹模及板料进行CAD建模。

(2)然后通过标准数据转换接口IGES 将曲面模型导入Dynaform中。建立对应模型及网格划分，如图2所示。

图2 有限元模型图

(3)凸模冲压速度为2 m/s，板料压边力为2 kN，工具间摩擦因数定义为0.12，进行模拟计算，模拟后的成形极限图如图3所示，厚薄图如图4所示。

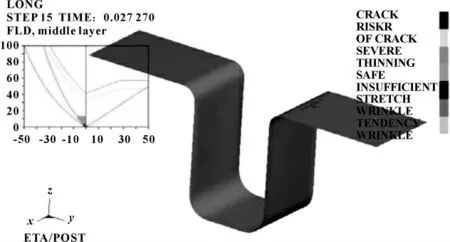
图3 成形极限图

图4 厚薄图

由图3可以看出:上述条件下，冲压成形后零件各部分均处于安全区域。图4显示零件的最小厚度为0.919 mm，变薄率在10%以内，所以只需考虑回弹而不用担心其他如拉裂、起皱等缺陷的产生。

回弹模拟结束后，以图5中θ1和θ2为评价指标[3]，测量相关回弹变形尺寸如表2所示。将文中得到的模拟结果与NUMISHEET’93的结果进行对比可以看出，文中得到的结果与会议给出的结果比较接近。因此文中采用的U形件弯曲回弹数值模拟技术是可行的。

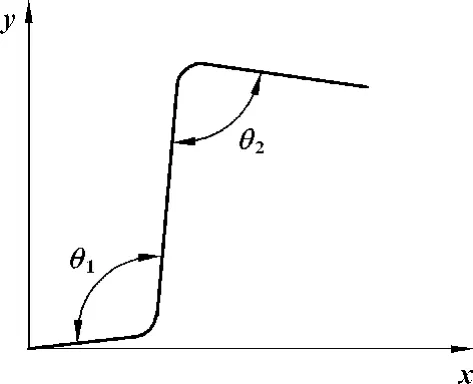
图5 回弹的评价方法

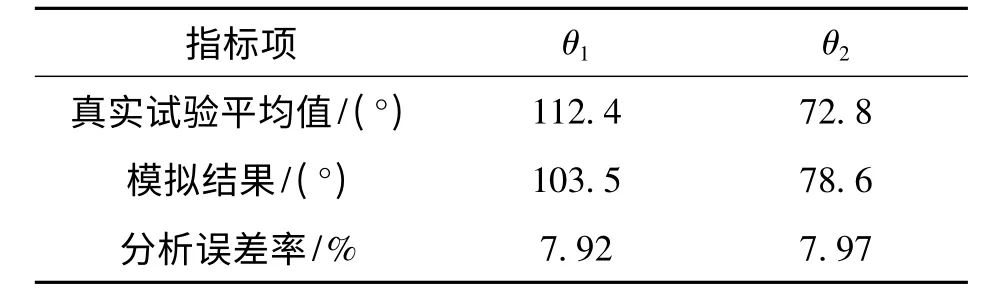
表2 真实试验结果与模拟结果

1.2 影响因子及水平的确定

影响U形件成形回弹的因子包括:冲压速度、压边力、摩擦因数、模具间隙、凹模圆角、相对弯曲半径[7]，根据相关的设计手册及设计经验，U形件成形回弹正交试验中影响因子水平选取如下:

(1)冲压速度。文中取冲压速度水平为2、3、4 m/s。

(2)压边力。文中取压边力水平为2、3、4 kN。

(3)摩擦因数。文中取摩擦因数水平为0.11、0.12、0.13。

(4)模具间隙。文中取模具间隙水平为1.05、1.1、1.15 mm。

1.3 正交表的选取及U形件成形正交试验结果

由于文中设有4个因子，而每个因子有3个水平，为了节省试验次数，一般应尽量选用较少次数正交表，现在选取L9 (34)。将上述试验参数代入正交表可得试验方案表如表3所示[8－9]。

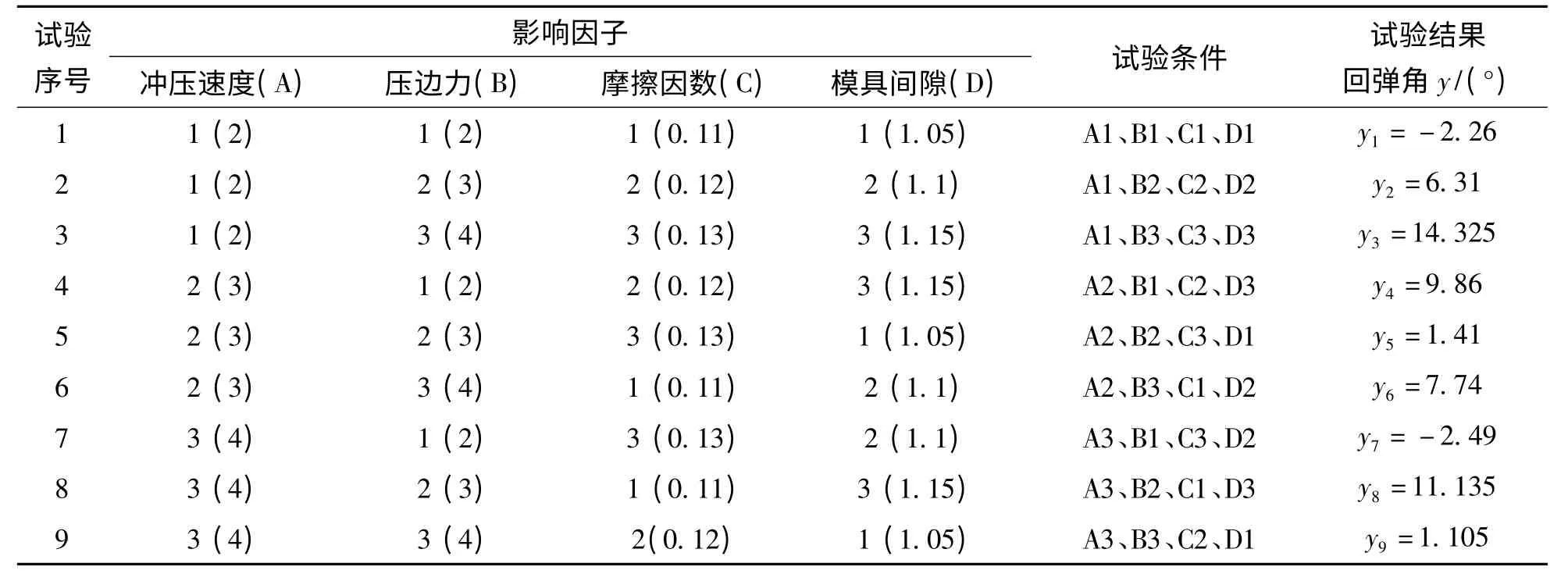
表3 试验方案及试验结果分析表

1.4 试验方案数据模拟

将表3中试验方案代入Dynaform 中以回弹角度y为响应因子进行回弹分析(如图3所示)，可得试验回弹结果如图6所示。

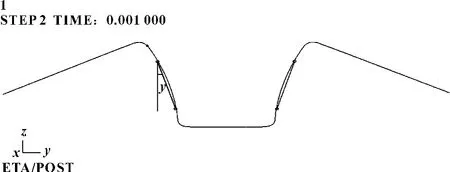
图6 回弹分析图

2 基于径向基函数代理模型建立及优化

径向基函数模型方法就是寻找f(x)，x∈Rn来近似n维变量实值函数F(x)，用φ(r)作为函数f(x)的基函数，φ(r)由x与每一个数据点xi径向距离r 决定，其基本思想是:首先确定一组样本点x=(x1，x2，…，xm)(i=1，2，…，m)，然后以这些样本点为中心，以径向基函数为基函数，通过这些函数的线性叠加来计算待测x 处的响应值。通过欧氏距离，径向基函数可以很容易地把一个多维问题转化成为欧式距离自变量的一维问题[10]。

径向基函数的基本形式如下:

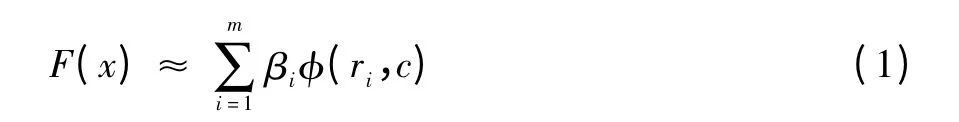
式(1)中:ri=‖x－xi‖是x与第i个采样点xi在设计空间的距离，φ(·)为基函数，‖·‖为欧氏范数，c为非负常数，β为距离基函数φ(·)的加权系数。由于一般情况下任何函数都可以表示成一组基函数的加权和，所以可以实现从输入样本到基函数输出之间的一种非线性映射[11]。

径向基近似模型一般可表达如下:

用式(2)作为预测模型时，它要满足如下的插值条件:

将式(3)代回式(2)，令rij=‖xi－xj‖(i，j=1，2，…，m)可以得到方程组:

文中用到的核函数多为二次函数，如下式所示:

式中:c是给定的大于零的常数参数，取核函数在c=1时的函数。

由式(4)、式(6)及表3可得:

式(4)在样本点不重合、且函数φ(r)为正定函数时存在唯一解，即:

所以由上可得径向基函数，利用MATLAB 中fmincon函数x优化计算，各参数取值范围为:1 ＜A ＜4，1 ＜B ＜4，0.11 ＜C ＜0.13，1.05 ＜D ＜1.15，可得优化参数:

A=2.885 6 m/s，B=3.044 2 kN，C=0.130 0，D=1.050 0 mm，y=1.172 9°

3 Dynaform 回弹的数值模拟验证

将优化参数A=2.885 6 m/s，B=3.044 2 kN，C=0.130 0，D=1.050 0 mm，y=1.172 9°，代入模型进行模拟仿真，测量回弹角y=1.28°，误差率为9.3%。

4 结束语

首先确定回弹角为响应因子，以压边力、冲压速度、摩擦因数、凸凹模间隙为影响因子，进行正交试验方案设计;然后利用Dynaform软件进行回弹模拟，得出不同试验方案的回弹角;用径向基函数建立代理模型，经MATLAB 中fmincon函数优化分析得出了优化的影响因子值及回弹角，然后将优化后的影响因子代入模型进行模拟，验证了文中介绍的方法的可行性。

【1】杨逢瑜，娄磊，王顺，等.基于改进的径向基函数神经网络混合控制在电液伺服系统中的应用[J].机床与液压，2009，37(9):187－189.

【2】吴宗敏.散乱数据拟合的模型、方法和理论[M].北京:科学出版社，2007.

【3】WANG Liping，BEESON Don，WIGGS Gene.A Comparison of Meta-modelling Methods Using Practical Industry Requirements[C]//AIAA 2006－1811.

【4】陆爽，侯跃谦.基于PCA 和径向基函数神经网络的滚动轴承故障模式的识别[J].机床与液压，2005(3):185－188.

【5】王征.一种新型径向基函数神经网络在模型辨识方面的应用[J].机床与液压，2005(12):130－131，51.

【6】徐雅东.U形件弯曲回弹预测及优化方法研究[D].天津:天津理工大学，2008.

【7】余国庆，鲁世红.板料弯曲回弹的有限元模拟影响因素研究[J].模具工业，2004(12):7－11.

【8】李学光，王惠伟，张树仁，等.基于正交试验法的切削参数优化研究[J].机床与液压，2011，39(8):17－19.

【9】黑学艳，郭津津，徐雅冬.正交试验法在U形件回弹数值模拟中的应用[J].机床与液压，2009，37(4):128－130.

【10】MCDONALD Dale B，GRANTHAM Walter J，TABOR Wayne L，et al.Global and Local Optimization Using Radial Basis Function Response Surface Models[J].Applied Mathematical Modelling，2007，31 (10):2095－2110.

【11】安治国.径向基函数模型在板料成形工艺多目标优化设计中的应用[D].重庆:重庆大学，2009.