电动负载模拟器抑制多余力的结构补偿控制

李瑞，王明艳

(中北大学信息与通信工程学院，山西太原030051)

在科学研究中，为了测试产品的性能指标，需要模拟出对象的实际工作环境，对产品施加与实际情况相对应的负载，从而真实地反映产品实际的性能，这就需要研制出高性能的加载系统，以便为新材料和产品的应用、为新技术的推广提供可靠的实验资料[1]。按照加载执行元件的不同，可分为机械式负载模拟器、液压式负载模拟器和电动式负载模拟器。

由于电液负载模拟器的污染大，维修困难，近年来，随着电机性能的不断提升、电力电子器件、电机驱动系统的发展、电机制造水平的提高，越来越多的伺服控制系统以永磁同步电动机作为执行元件，因此必须采用电动加载方案。电动负载模拟器对于缩短系统研制周期、节约研制经费、提高可靠性和成功率有着重要意义[2]。

1 电动负载模拟器系统硬件组成

一个完整的电动负载模拟器应由加载电机、扭矩传感器、联轴器、驱动器、控制器、上位机等几部分组成，如图1所示。

图1 电动负载模拟器结构框图

控制器接收仿真计算机发出的指令信号及扭矩传感器发回的力矩反馈信号，利用给定的控制算法计算出下一时刻的控制量，通过驱动器作用在加载电机上，产生相应的力矩输出施加到舵机上，扭矩传感器再将作用在舵机上力矩值实时反馈给控制器，为计算下一时刻控制量提供依据。

2 系统模型的建立

加载电机模型。加载电机选择永磁直流力矩电机，可以使得电动加载系统获得良好的动态、静态性能。

直流力矩电机的电压平衡方程为:

式中:Em为电枢反电动势，它是当电枢旋转时产生的反电势，其大小与激磁磁通及转速成正比，方向与电枢电压Um相反。则反电动势Em可以写为:

直流力矩电机的转矩平衡方程为:

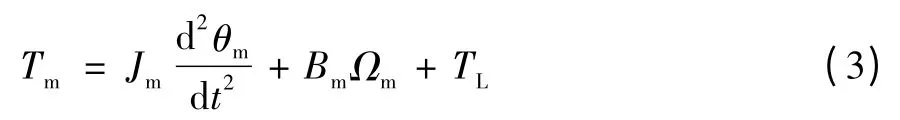
电磁转矩Tm可表示为:

式中:Um为电枢电压，KT为转矩系数，Ke为反电动势系数，Rm为电枢回路总电阻，Lm为电枢回路总电感，Ωm为电机角速度，θm为电机角位移，Bm为电机阻尼系数，Jm为等效转动惯量，im为电枢电流。

转矩传感器模型。转矩传感器连接加载电机和舵机的输出轴，可将传感器两端的微小角度形变转化为转矩信号输出。假设传感器的刚度系数为Kf，传感器两端的角度差Δθ=θm－θr，则输出的转矩可表示为:

PWM 驱动装置模型。PWM变换器是具有饱和特性的拟线性放大器，当大功率晶体管的开关频率远远大于电动机的工作频率时，PWM 驱动装置的输出信号中交流分量的影响很小，可以近似认为PWM 驱动装置为一个比例环节，其放大倍数为KPWM。

由以上表达式可得电动加载系统的动态结构图，如图2所示。

图2 电动加载系统动态结构图

由图2可得加载电机输出转矩的传递函数表达式为:

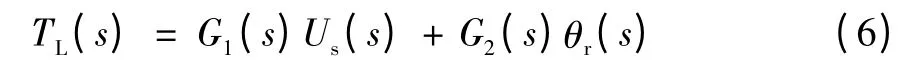
其中:

可见:输出力矩由两部分组成，后一部分带有明显的微分特性，被加载对象的角速度、角加速度、角加速度的变化率的扰动引起，这就是所谓的多余力矩[3－5]，多余力矩的存在会破坏加载电机对给定载荷曲线的跟踪精度。

3 消除多余力矩

文中采用结构不变性原理来消除多余力矩，使用双通道正负抵消，进行前馈控制来消除多余力矩，并分析以下两种消除多余力矩方法的局限性，提出改进的结构不变性原理来消除多余力矩。

3.1 被加载对象角位移前馈补偿法

对于电动负载器来说，最直接的扰动补偿是利用被加载对象的角位移本身进行补偿。系统结构图如图3所示。

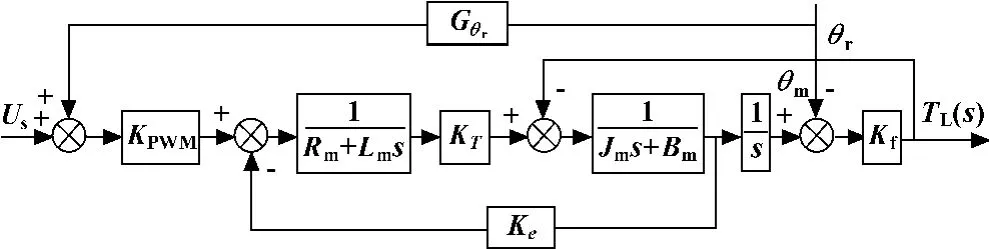
图3 角位移前馈补偿法结构图

由结构图和结构不变性原理可以得到:

多余力矩可以完全被抑制，但事实上Gθr的实现有一定的难度，因为高阶的纯微分环节容易引入干扰。加入补偿环节后，大部分多余力矩可以被消除。

3.2 负载模拟器电流反馈补偿法

电流Im反馈扰动补偿法，就是为了降低系统的微分阶数。系统结构图如图4所示。

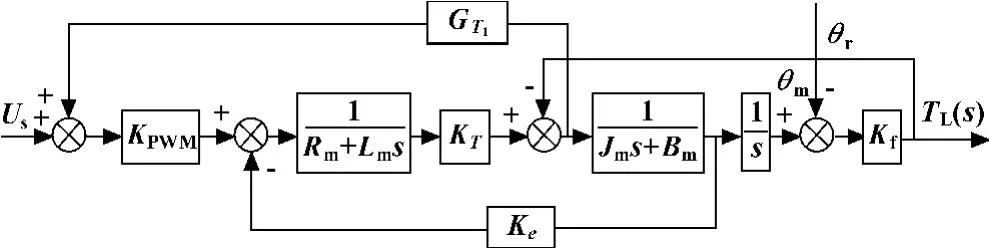
图4 电流反馈补偿法结构图

在设计补偿环节时，负载等效刚度比较大，在低频段加载中可以近似认为负载模拟器的角速度等于被加载对象的角速度[6]。

代入上式可得:

实际上，基于结构不变性原理的被加载对象角位移前馈补偿法，是用角位移信号微分得到速度信号，然而微分得到的加速度信号和相位滞后严重影响了信号质量。对于负载模拟器的角速度反馈补偿法，由于要求速度近似相等，事实上有一定的条件，需要刚度无穷大。限制了其应用，有一定的局限性。

3.3 被加载对象的电流前馈补偿法

在抑制多余力矩的研究中，常规方法都着眼于加载系统，忽视了被加载对象系统。作者从电动负载模拟器和舵机两部分出发，在被加载对象角位移前馈的基础上，提出被加载对象电流前馈补偿法，克服以上两种方法的局限性，使补偿环节微分阶数降低两阶，降低了实现难度。系统框图如图5所示。

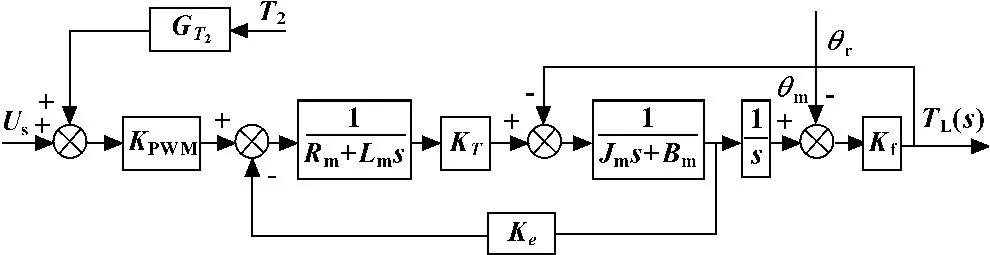
图5 电流前馈补偿法结构图

代入上式，可得:

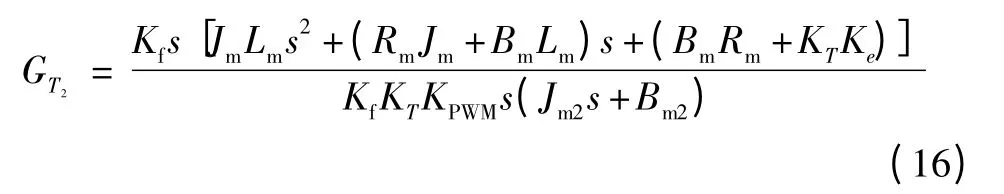
电动负载模拟器是一个复杂的机电一体化控制系统，虽然目前有神经网络控制等智能控制理论的应用文献介绍，但考虑到工程中的实际应用性，仍以成熟的PID控制来设计，同时采用输出力矩变化速度负反馈来增加阻尼，降低超调量，提高系统的稳定性，基于被加载对象的电流前馈补偿法来提高控制系统的快速性，减小多余力矩。

3.4 仿真分析

基于控制策略的介绍和分析，采用改进的前馈方法消除舵机运动在加载系统输出上的扰动，用微分负反馈、力矩反馈、前向通道控制器的复合控制方法来设计系统。经过以上的系统分析，经过拉普拉斯变换，可得整个电动负载模拟器的控制结构原理图如图6所示。

图6 系统控制结构图

参数如下:Rm=4.5 Ω，Lm=7 mH，Jm=0.15 kg·m2，Bm=0.33 m·s/rad，Ke=4.85 V·s/rad，KT=6 N·m/A，Kf=10 N·m/rad，Kv=0.05。

根据以上原理图建模，动态测试结果如表1所示。

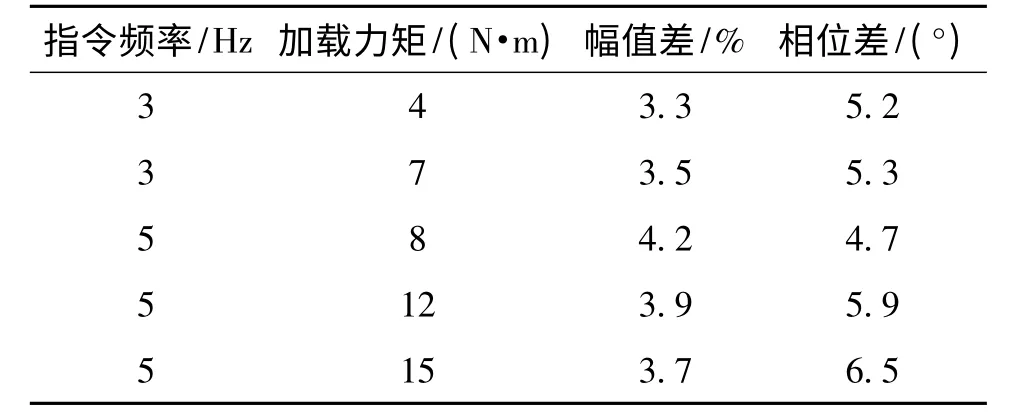
表1 动态测试结果

有舵机扰动，加入正弦信号的响应:

(1)给定信号为:T=4sin(6πt)，输出与输入结果如图7所示。

(2)给定信号为T=6sin(10πt)，输出与输入结果如图8所示。

根据以上仿真结果可以看出:加入改进的结构不变性原理的复合控制能够很好地消除多余力矩，使输出能够快速稳定地跟踪给定，减小了误差，符合舵机加载系统的指标要求。

图7 正弦响应图(T=4sin(6πt))

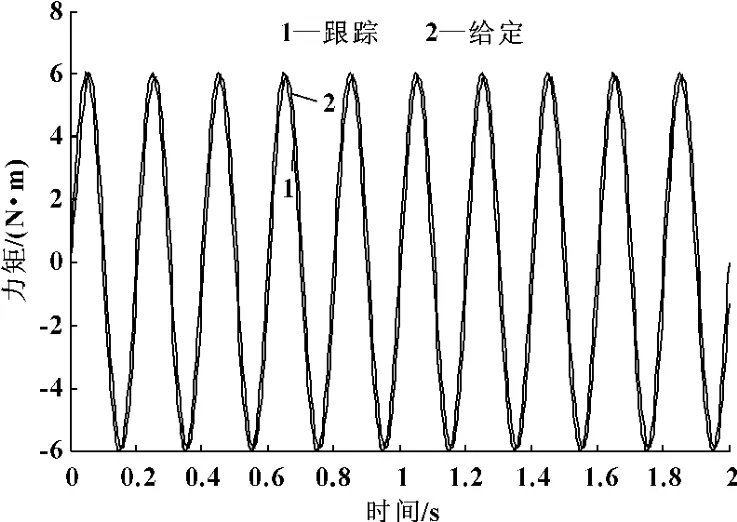
图8 正弦响应图(T=6sin(10πt))

4 结论

电动负载模拟器的多余力矩是由于舵机的位置扰动引起的，采用改进型结构不变性原理能够很好地抑制扰动，误差很小，满足要求，而且基于控制算法的简单性以及技术上的成熟性、可行性，在工程实际应用中有很好的参考价值。

【1】王述运.结构不变性原理在减摇鳍加载台中的研究分析[D].哈尔滨:哈尔滨工程大学，2004.

【2】李成功，靳红涛.电动负载模拟器多余力矩产生机理及抑制[J].北京航空航天大学学报，2006，32(2):204－208.

【3】邹海峰.飞行器舵机电动伺服加载系统研究[J].系统仿真学报，2004，16(4):657－659.

【4】杨新峰，苑秉成.深弹舵机电动力加载控制系统的建模与仿真[J].计算机仿真，2010，27(1):13－17.

【5】马志伟，杜经民，余祖耀.电动加载系统多余力特性分析[J].机床与液压，2007，35(6):188－190.

【6】王明彦.电动负载模拟技术的研究[D].哈尔滨:哈尔滨工业大学，2004.