双激振器液控惯性振动筛启动过程分析
2013-03-16窦鹏马胜钢冯静刘兰荣刘救世张青召
窦鹏,马胜钢,冯静,刘兰荣,刘救世,张青召
(郑州大学机械工程学院,河南郑州450001)
液控惯性振动筛是一个机、液混合系统,其启动过程是一个复杂的变化过程。目前在设计大型振动筛时,由于缺少对振动筛启动过程的理论研究,设计者常依赖于设计经验和类比方法,设计的大型筛常出现动力过小或过大的情况。动力太小会造成振动筛启动困难或长时间停留在共振区造成关键零件的破坏;动力过大会造成振动筛启动后稳幅振动时能源的浪费[1-2]。为了研究大型筛的启动过程,作者利用功率键合图法建立了振动筛系统的数学模型并进行了仿真分析,得到了一些有益的结论。
1 液控振动筛的物理模型
文中研究的液控振动筛的物理模型如图1所示。驱动系统采用两套独立的、相同的液压驱动系统(图2为简化的系统之一),由液压泵直接驱动液压马达带动联轴器驱动激振器旋转,溢流阀用以控制液压系统的最高压力,如图2所示。此液压驱动系统能较方便地测量系统的压力和流量,容易测算出任意时刻的驱动功率,同时保证了两个激振器受到足够的驱动力矩,并能方便实现自同步旋转。两组激振器以如图1所示位置安装,物料从振动筛左侧送入筛箱3,在激振器1 和激振器2的联合作用下实现筛分同时又可以实现物料的输送。筛箱3通过主振弹簧4 支撑在减振体5 上,减振体和地面之间有减振弹簧6相连[3]。

图1 振动筛结构示意图

图2 液控惯性振动筛系统简图
2 液控振动筛的数学模型
(1)数学模型的建立
在建立液控惯性振动筛数学模型的过程中,对物理模型进行了一些简化,把筛箱和减振体简化成没有弹性的刚体。根据相关文献的计算和实验结果,筛箱扭振的摆角很小并且在启动后短时间内即衰减为零,因此建立键合图时忽略了筛箱和减振体的扭振。另外,文中把筛箱与减振体的运动分解为x方向和y方向的振动,分别对两个振动方向进行数学建模。其中x方向为两激振器中心连线的方向,y方向为与x方向垂直的方向。这样处理能更加直观地表达出振动筛的运动情况和两个激振器的同步过程[4]。
通过分析研究对象的物理模型和主要影响因素,按照功率键合图的建模原则,可以建立液控振动筛的键合图模型,如图3所示[5]。

图3 液控惯性振动筛系统功率键合图
根据由键合图列写状态方程的原则,选择键2、32、26、29、53、57的广义位移q2、q32、q26、q29、q53、q63和键8、38、20、27、49、58的广义动量p8、p38、p20、p27、p49、p58为状态变量。其中的键12、17、42、47为非独立储能元件,它们对应的4个变量为非独立的状态变量p12、p17、p42、p47,可以用前面的12个状态变量表示出来。
根据键合图列写出状态方程如下:


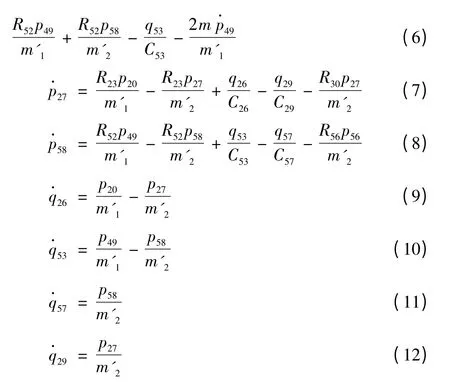
式中:q2,q32分别为液压泵与马达间管道容腔中因压力升高需补充的油液体积;θ1,θ2分别为激振器1、2 转过的角度;p8,p38分别为激振器1、2的广义动量;p49,p20分别为筛箱在x、y方向的广义动量;p58,p27分别为减振体在x、y方向的广义动量;q53,q26分别为主振弹簧在x、y方向的广义位移;q57,q29分别为隔振弹簧在x、y方向的广义位移;f1,f2分别为液压泵1、2的输入流量;C2,C32分别为液压泵至液压马达段的液容;m1,m2分别为激振器1、2的等效质量,均为m;J为激振器与偏心轴的转动惯量;m'1,m'2分别为筛箱和减振体的质量;C53,C26分别为主振弹簧在x、y方向的柔度;C57,C29分别为隔振弹簧在x、y方向的柔度;R52,R23为筛箱与减振体之间的阻尼系数;R56,R30为地基与减振体之间的阻尼系数。
(2)数学模型中关键参数计算
文中仿真模型主要参数的选取如下:f1=f2=6.848×10-4m3/s;R3=R33=8.01×1010N·s/m5;R5=R35=1.05×1011N·s/m5;V=4.28×10-5m3/s;C2=C32=4.1×10-13m5/N;J=0.84 N·m·s2;m=39.6 kg;r=0.112 m;m'1=3 385 kg;m'2=3 946 kg;R68=R70=0.012;R23=25 630;R30=25 630;R67=R69=7.798×10-4;C53=4.383×10-5m/N;C26=2.184×10-6m/N;C29=2.826×10-6m/N;C57=5.372×10-5m/N;R52=25 630;R58=25 630。
3 液控振动筛启动过程的仿真分析
利用MATLAB软件对双激振器液控振动筛的启动过程进行了仿真分析,得到了该系统启动过程中关键参数的实时变化情况。仿真时,假定两激振器的初始相位角不同,以验证两激振器在启动过程中是否实现了等速反向回转,即是否能够实现振动同步。该例中选用θ1=0,θ2=5π/3。仿真结果见图4—9。
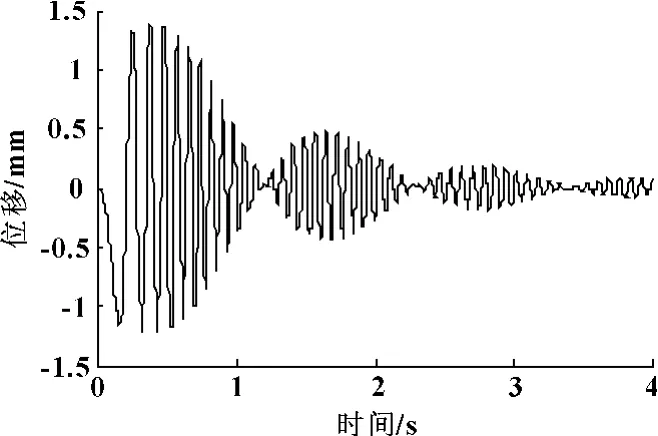
图4 筛箱在x方向的位移
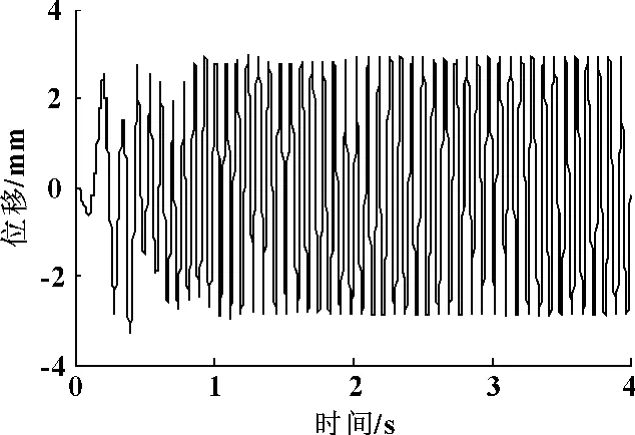
图5 筛箱在y方向的位移

图6 两激振器相位角之差

图7 减振体在x方向的位移
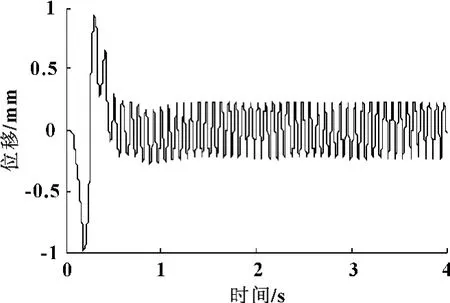
图8 减振体在y方向的位移

图9 所需驱动功率值
4 仿真模型的实验验证
仿真模型需要实验进行验证。作者对双激振器的同步行为进行了实验,可观察到两激振器在启动后5 s左右实现了同步。然后对筛箱的稳态振幅进行了实验验证。实验利用简单实用的振幅牌来获取筛箱上12个采样点的稳态振幅,实验数据如表1所示。

表1 筛箱在x方向、y方向的实验振幅值 mm
从实验数据可以看出:仿真结果与实验结果基本吻合,但仍存在一些误差。误差产生的原因是忽略因素引起的误差、参数取值产生的误差、线性化产生的误差和实验系统的误差等。
5 结论
通过上述的论证分析和实验研究,可以得出以下结论:
(1)振动筛启动时所需的驱动功率远大于正常工作值的驱动功率,约为正常工作时的5~6倍。
(2)启动时的驱动功率越大,振动筛快速通过共振区的能力越强,最大程度地减少了关键件震动破坏的可能性。液压驱动能较大幅度改变驱动功率,使其成为振动筛动力配置的较好选择。
(3)液压驱动系统和激振器本身的参数差别越小,两激振器越容易实现振动同步。
【1】马胜钢,祁建中,邹杜,等.大型振动筛液控驱动系统的应用研究[J].机床与液压,2002(4):75-76.
【2】孙伟,李朝峰,马辉,等.直线振动筛可视化设计计算系统的研究与开发[J].机床与液压,2007,35(9):3-6,60.
【3】张建立,冯静,马胜钢,等.粒度精确分级筛的运动参数研究[J].矿山机械,2009(21):97-100.
【4】邹杜.液控惯性振动系统的理论分析与实验研究[D].郑州:郑州大学,2001:10-30.
【5】王中双.键合图理论及其在系统动力学中的应用[M].哈尔滨:哈尔滨工程大学出版社,2007.
