卸砖码垛重载机器人的机构设计和运动学分析
2013-03-16李跃刘知贵谭明中
李跃,刘知贵,谭明中
(1.西南科技大学制造学院,四川绵阳621010;2.西南科技大学研究生部,四川绵阳621010;3.资阳市精工砖机有限公司,四川资阳641301)
随着机器人技术的发展,机器人的应用范围越来越广泛,应用于自动化生产线的码垛机器人就是其中的一个例子[1]。工业码垛机器人属于典型的机电一体化高科技产品,对企业提高生产效率、增长经济效益、保证产品质量、改善劳动条件、优化作业布局贡献巨大,其应用的数量和质量标志着企业生产自动化的先进水平[2]。目前,常用的码垛机器人类型有直角坐标型、圆柱坐标型、水平关节型、垂直关节型。文献[3-5]所描述的码垛机器人均采用垂直关节型平行四连杆机构,采用该结构使控制算法简单,机器人定位精度高,但由于该结构无法装载缓冲装置,抗冲击性差,因此不能够承受大于5 000 N的重型负载。而现代制砖生产线要求卸砖码垛设备能够承受超过6 000 N的负载,一般的码垛机器人不能满足要求。因此,在国内卸砖码垛设备的研发仍处于初级阶段。
作者及其团队和相关企业合作,经过攻关,利用视觉伺服技术,成功研制出适合砖窑卸砖码垛的重载机器人的实验样机。下文对该机器人结构和运动学进行介绍。
1 机器人结构设计
机器人工作要求:将砖从位于回车道上的某一指定位置的窑车上逐层卸载。卸载过程中,将间隔排列的砖合拢后堆在指定位置的指定型号的货车上,完成一次卸装任务,之后进行下一次工作循环,直到此次装卸任务完成。以目前最小规格2 500 mm的窑车为例,其砖堆为9 垛,每一垛为3×8 纵横交错排列,砖的规格为2.5 kg/块,按此计算,机器人一次卸砖码垛的负重需要达到5 400 N,因此该机器人采用带氮气缓冲装置、抗冲击能力强的铰链式四连杆结构。其结构如图1所示。
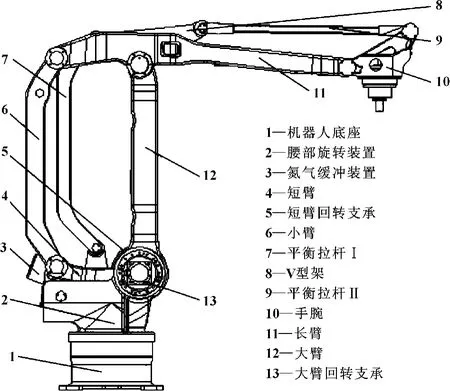
图1 机器人结构图
该机器人主要由底座、腰部、臂部、手腕组成。底座为整个机器人本体的安装基础,腰部由一个轴线垂直于水平面的旋转关节与底座联接,为机器人臂部、手腕提供支撑和整体旋转驱动力。臂部主要包括大臂回转支承、短臂回转支承、大臂、小臂、长臂和短臂。大臂回转支承包括支承架、减速器和交流伺服电机,它为大臂提供支撑和旋转驱动力矩。短臂回转支承和大臂回转支承具有相似的结构,它为短臂提供支撑和驱动力矩。大臂和短臂的回转中心重合,大臂和小臂相互平行且长度相等,从而保证了大臂、小臂、长臂铰接部分和短臂一同构成平行四边形。该结构增加了整个臂部的刚度,且具有行程放大功能,即以较小的驱动行程实现机器人末端较大的工作行程,从而可以满足卸砖码垛作业对大工作空间的性能要求。氮气缓冲装置的一端铰接在大臂上,另一端铰接在腰部回转支承座上,为大臂的速度突变提供缓冲,使整个铰链四连杆机构的抗冲击性能大大加强。整个铰链式四连杆结构是该机器人的关键部分,直接决定了该机器人的承载能力,各连杆参数的选择及其安装的相对位置将直接影响机器人的工作空间范围。手腕与长臂采用铰链式连接方式,并且通过一个特别设计的七连杆吊环平衡装置实时保持对地水平。手腕处对地垂直安装一个减速器和交流伺服电动机,为手爪的旋转提供驱动力矩。手腕对手爪采用预留法兰盘接口,方便手爪的安装和维修。
2 机器人运动学分析
2.1 运动学正解
文中所研究的机器人由4个旋转关节和4个连杆组成,故为4 自由度机器人。对该机器人的描述采用传统的D-H 方法[6]。用D-H 法建立的各连杆坐标系如图2所示,D-H坐标系对应的参数如表1所示。
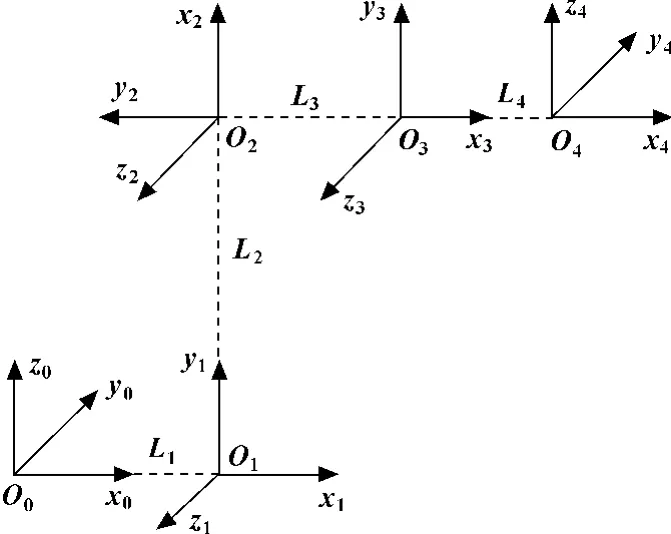
图2 机器人D-H坐标系
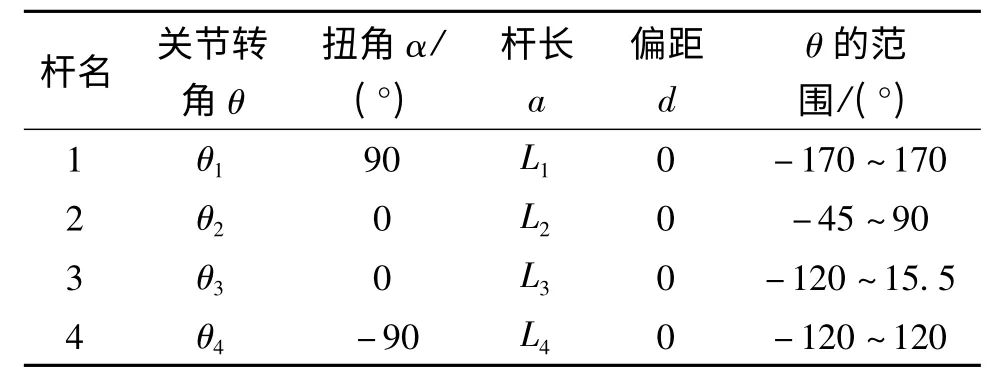
表1 机器人杆件参数
首先根据坐标系建立的方法和各参数的意义,建立i 系和i-1坐标系的齐次变换矩阵[7]

式中:θi为关节i的旋转角;αi为关节i 和i+1的扭角;di是关节i的偏距;Li是杆i的长度;i=1,2,3,4。
将表1中的参数一次代入式(1),得到

式中:si=sinθi,ci=cosθi,以下同样。则
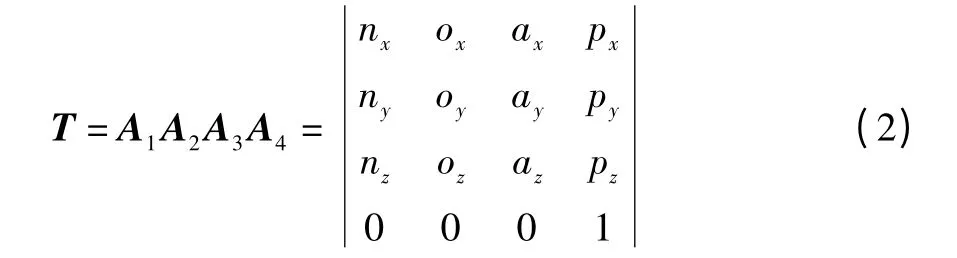
其中:
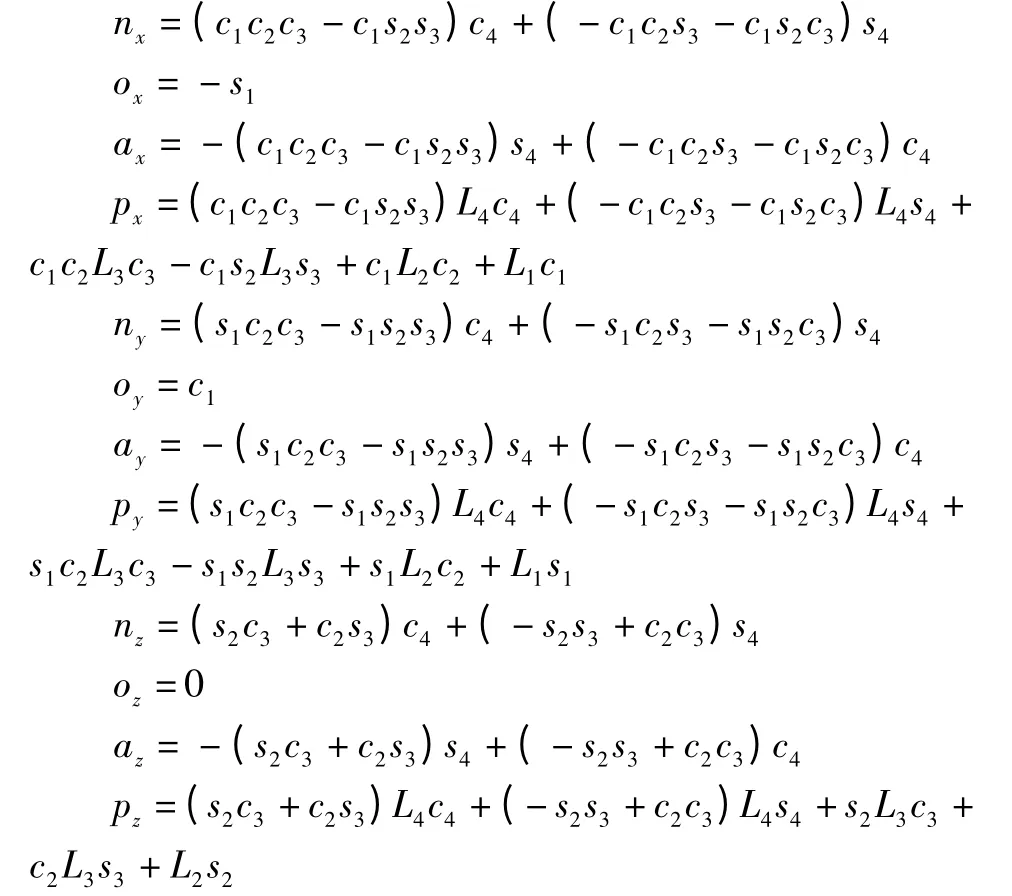
这样由T可以得到机器人末端的位置和姿态,T中只包含变量θi,其中θ1、θ2、θ3控制机器人末端位置,θ1、θ4控制机器人末端姿态。
2.2 运动学逆解
运动学逆解问题是已知机器人末端的位姿,求出相应的关节变量。机器人运动学逆解常规方法是采用paul的代数法进行求解[8],该方法的主要思想是:在等式两边同时乘以前一个变换矩阵的逆矩阵求出一个未知参数,即A-11 T=A2A3A4,求出θ1,然后利用求出θ2,以此类推,求出θ3、θ4。采用此方法,虽然思路简单,但是需要多次求逆矩阵,过程较为繁杂。作者提出一种避免多次逆矩阵相乘的新方法,减少了求逆次数和计算量。具体方法为:用左乘T后再右乘即

在方程(3)中,左边
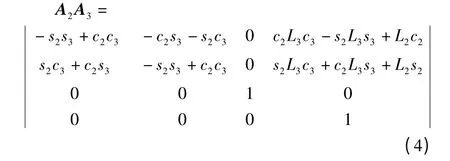
右边

其中:

根据式(4)和式(5)可以求出θ1、θ2、θ3、θ44个关节变量。
(1)求θ1。令式(4)和式(5)的(1,3)矩阵元素对应相等,可得
-c1ox-s1oy=0
解得

(2)求θ4。令式(4)和式(5)的(3,1)矩阵元素对应相等,可得
(s1nx-c1ny)c4-(s1ax-c1ay)s4=0
解得

(3)求θ3。令式(4)和式(5)的(2,1)矩阵元素对应相等,可得
s2c3+c2s3=nzc4-azs4
解得

同时可得

(4)求θ2。令式(4)和式(5)的(2,4)矩阵元素对应相等,可得
s2L3c3+c2L3s3+L2s2=-nzL4+pz
结合式(9)可以解得

这样就求得该4 自由度机器人的4个封闭解,没有奇异解。如果机器人存在多解,则应该根据实际需要选取最符合的一组解。
3 机器人运动位姿的数值验证
3.1 正解的验证
首先根据图2给定机器人初始位置4个自由度的输入:θ1=0、θ2=90°、θ3=-90°、θ4=0,L1=215 mm,L2=1 600 mm,L3=1 600 mm,L4=250 mm。代入式(2),利用Maple 计算出机器人末端的位姿为:

因θ1=0 和θ4=0,机器人姿态并没有改变。初始位置时,px=L1+L3+L4=2 065,py=0,pz=L3=1 600。因此,计算结果与末端在初始位置时的实际位姿完全一致,由此验证了正解模型的正确性。
3.2 逆解的验证
假定机器人4个关节的输入角度分别为:θ1=30°、θ2=45°、θ3=-60°、θ4=30°,代入式 (2),得机器人末端的位姿为:

将上述齐次坐标变换矩阵中机器人末端位姿代入公式(6)—(10)得:θ1=30.000 1°、θ2=45.000 1°、θ3=-60.000 1°、θ4=30.000 1°。与4个自由度的输入一致,此计算误差约为10-4,逆解的正确性得到验证。
4 结束语
针对某企业生产线的实际需求,设计了一种铰链4 连杆4 自由度砖窑卸砖码垛重载机器人的实验样机。推导了该机器人的运动学模型,求出了运动学正逆解。在求逆过程中,提出了一种新的简便算法,避免了大量的矩阵求逆和相乘,减少了计算量,快捷地计算出相应结果。同时对正逆解进行了数值仿真,验证了其正确性。
【1】刘扬,高志慧,贠超,等.混联码垛机器人运动学分析与仿真[J].机械与电子,2010(3):57-60.
【2】张丰华,韩宝玲,罗庆生,等.基于PLC的新型工业码垛机器人控制系统设计[J].计算机测量与控制,2009,17(11):2191-2196.
【3】李成伟,贠超.码垛机器人机构设计与运动学研究[J].机械设计与制造,2009(6):181-183.
【4】苏海新,韩宝玲,罗庆生,等.基于PMAC的工业码垛机器人控制特性研究[J].机械与电子,2009 (9):58-60.
【5】黄泳波.码垛机吊臂连杆机构的运动分析与优化设计[J].起重运输机械,2008(3):15-17.
【6】DENAVIT J,HARTENBERG R S.A Kinematic Notation for Lower-pair Mechanisms Based on Matrices[J].ASM Journal of Applied Mechanics,1992,22(2):215-221.
【7】朱世强,王宣银.机器人技术及应用[M].杭州:浙江大学出版社,2001.
【8】王仲民,蔡霞,崔世钢.一种四自由度机器人的运动学建模[J].天津职业技术师范学院学报,2003(13):1-4.
