基于PSO算法优化BP神经网络的数控机床热补偿

任兵，任小洪，李国志

(四川理工学院自动化与电子信息工程学院，四川自贡643000)

随着精密加工技术的广泛应用，对数控机床加工精度的要求日益提高。大量研究表明，热误差是数控机床等精密加工机械的最大误差源，占总误差的40%～70%左右[1]。要减小热误差，提高加工精度，热误差补偿是一种有效的措施。文献[2]中指出数控机床热误差补偿技术已经成为以误差补偿技术为代表的现代精密工程的重要技术支柱之一。目前采用的热误差补偿方法除了经验公式法、实验法、回归法等外，文献[3]中介绍了一种基于BP神经网络的热误差补偿方法，并分析了该方法的可行性。BP神经网络是一种多层前馈型神经网络，可以实现从输入到输出的任意非线性映射，但由于BP神经网络热补偿方法初始化网络权值的随机性，在实际应用中，难以确定一组较好的初始权值，并且BP神经网络具有学习收敛速度慢、训练时间长、易陷于局部极小[4]等问题。

粒子群优化算法 (Particle Swarm Optimization，PSO)是计算智能领域的一种群体智能的优化算法，该算法最早由KENNEDY 和EBERHART 在1995年提出[5]。PSO算法具有收敛速度快、易于实现、不需要目标函数的梯度信息、没有许多参数需要调整等优点。经PSO算法优化后的BP神经网络，充分利用神经网络的学习能力和PSO算法的优点，既能提高神经网络的学习能力，又能增强神经网络的泛化性能和预测能力。

作者将粒子群优化算法与BP神经网络相结合，提出一种基于PSO算法优化BP神经网络、建立热补偿模型的误差补偿方法，对数控加工中心的热误差进行实时补偿。

1 PSO优化BP神经网络

1.1 PSO算法

PSO算法源于对鸟类捕食行为的研究。该算法首先初始化一群粒子，然后通过迭代寻优找出最优解。每一次迭代过程中，粒子通过跟踪个体极值Pbest和群体极值Gbest更新自身的速度和位置。

假设在一个D维的搜索空间中，由n个粒子组成的种群X=(X1，X2，…，Xn)。其中第i个粒子表示为一个D维的向量Xi=(xi1，xi2，…，xiD)T，代表第i个粒子在D维搜索空间中的位置。根据目标函数即可计算出每个粒子位置Xi对应的适应度值。第i个粒子的速度为vi=(vi1，vi2，…，viD)T，其个体极值为Pi=(Pi1，Pi2，…，PiD)T，种群的全局极值为Pg=(Pg1，Pg2，…，PgD)T。

在每一次迭代过程中，粒子通过个体极值和全局极值更新自身的速度和位置，更新公式如下[5]:

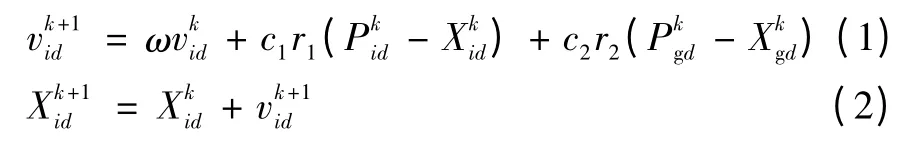
式中:d=1，2，…，D;i=1，2，，…，n;k为当前迭代次数;vid为粒子的速度;c1和c2为非负的常数，称为加速度因子;r1和r2为分布于[0，1]之间的随机数;ω为惯性权重。

为了更好地平衡算法的全局搜索能力，根据文献[6]，ω 按公式(3)进行更新:

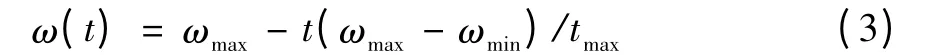
式中:t为迭代次数，tmax为最大迭代次数;ωmin为最小惯性权重，ωmax为最大惯性权重。

1.2 PSO优化BP神经网络分析

用PSO算法优化BP神经网络的目的就是通过PSO算法得到更好的BP网络初始权值和阈值。其基本思想就是用粒子群的位置向量代表网络的全部初始权值和阈值，初始随机产生N个微粒群，然后依照粒子群优化算法步骤，通过迭代寻优寻找全局最优位置向量，即最优的BP神经网络初始权值和阈值，使式(4)的均方误差指标达到最小，即适应值达到最小。将全局最优位置向量作为BP神经网络的初始权值和阈值，使用BP神经网络算法根据这些权值和阈值进一步寻优，从而得到网络权值和阈值的最优值。

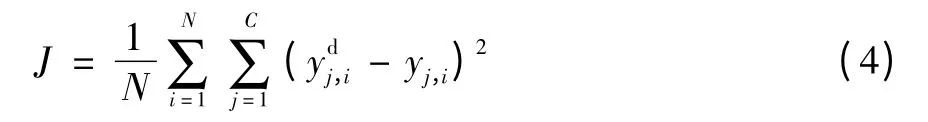
PSO-BP神经网络算法流程如图1所示。

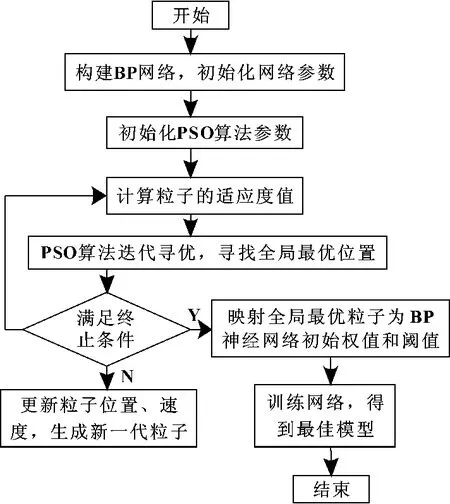
图1 PSO-BP算法流程

2 热误差补偿的实现

2.1 基于嵌入式的热补偿系统

图2是基于嵌入式的热误差补偿系统总体框图，该补偿系统以三星公司设计的低功耗、高集成度、基于ARM920T 核的16/32位RISC 微处理器S3C2440A为核心，搭建外围电路，构成补偿系统的硬件平台，以嵌入式Linux操作系统为核心搭建软件环境，在此基础上开发应用程序以及控制界面等。运用PSO算法优化后的BP神经网络建立误差补偿模型，将误差补偿模型固化到ARM 存储单元中。通过实时采集温度数据和位置误差数据，然后根据建立的误差模型计算出综合误差补偿值，将误差补偿值通过通信接口送入机床数控系统，数控系统根据补偿值对刀架或工作台进行附加运动来修正误差以完成实时补偿。热补偿系统需要实现PSO-BP神经网络建模、温度数据实时采集、误差数据采集、补偿值计算、显示温度数据和温度采集通道号以及补偿器与数控系统通信等功能。

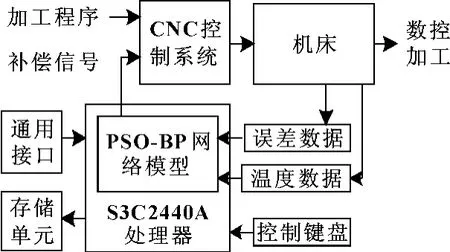
图2 热误差补偿系统总体框图

2.2 实验数据检测方法

基于神经网络建立误差补偿模型，首先需要获得大量用于网络训练和测试的实验数据。以GMC4000H/2 五坐标横梁移动龙门加工中心y轴为研究对象，介绍实验数据的检测方法。数据检测方法是:首先在引起热误差的关键温度点安装温度传感器，根据情况总共安装了8个温度传感器，测量包括电机外壳、上轴承座、十字滑座右、环境温度等8 路温度数据，然后安装激光干涉仪用于检测机床对应时刻的位置误差。机床开机起，首先测量一次温度数据和热误差数据，然后每行走170 mm 进行一次热误差测量，单向总行程为3 400 mm，热误差数据包括y轴正向和负向行走的数据。每间隔20 min 重复数据的采集。总共采集了21组温度数据和误差数据，其中包括升温和降温的温度数据和误差数据。

3 热补偿建模及仿真结果分析

3.1 PSO-BP神经网络建模

采用经 PSO算法优化后的BP模型对GMC4000H/2 五坐标横梁移动龙门加工中心热补偿进行研究。根据图1的算法流程图，首先需要确定BP神经网络的结构，分析测量的温度数据，从中选择温度变化较大的电机外壳、上轴承座和十字滑座右温度数据作为神经网络的输入，另外将刀具当前时刻位置距离刀具的初始时刻位置的距离也作为神经网络的输入，因此神经网络输入层的个数确定为4个，又通过定理[7]可计算隐含层的个数为(2N+1)=2×4+1=9个，最终确定BP神经采用4－9－1 结构，即4个输入层节点、9个隐含层节点、1个输出层节点。BP神经网络拓扑结构如图3所示。BP神经网络训练时使用的输入输出数据是在机床运行时测量得到的温度和误差数据，从测量的数据中抽取一部分用来训练网络，另一部分用来测试网络。BP神经网络训练参数设置如下:最大步数1 000，学习率0.1，学习目标0.001。PSO算法参数初始化如下:迭代步数50，种群规模40，加速度因子c1=c2=2，由文献[8]确定维数D=4×9+9×1+9+1=55。

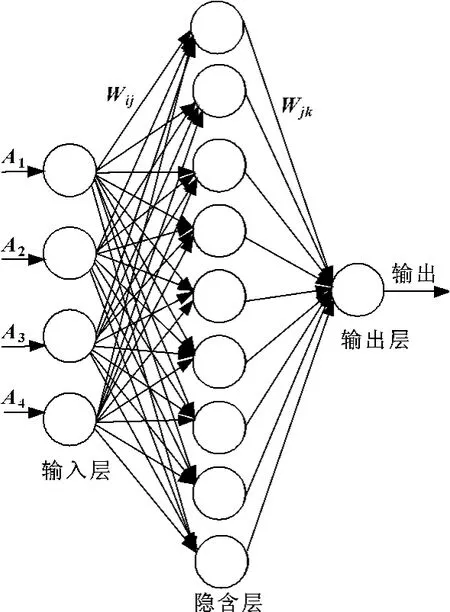
图3 BP神经网络拓扑结构

3.2 仿真结果分析

根据上述分析，将电机外壳、上轴承座和十字滑座右3个温度点数值以及刀具当前时刻位置距离初始时刻位置的距离的特征参数对应的数据通过MATLAB仿真，得出数据拟合情况和误差补偿效果如图4和图5所示。

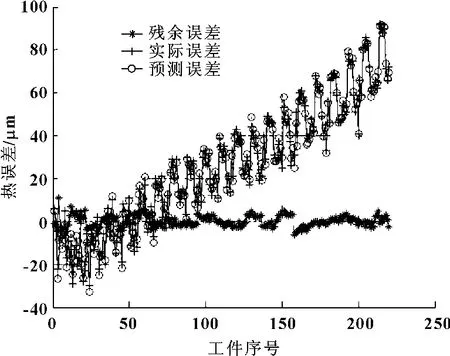
图4 PSO-BP 补偿效果

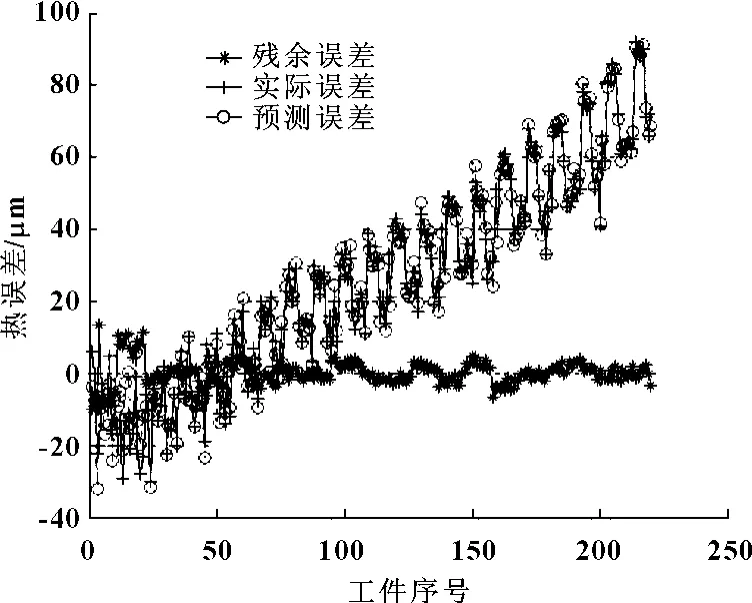
图5 BP 补偿效果

图4为经PSO算法优化后的BP神经网络训练数据后得到的补偿效果图，可见:经热误差补偿后，残余误差范围为:－6.442 1～11.152 4 μm，拟合性能好，预测能力强。图5为普通BP神经网络训练后得到的补偿效果图，其残余误差范围为:－9.964 9～13.528 3 μm。对比图4和图5可知:经PSO算法优化后的BP神经网络残余误差范围更小，补偿效果更好。结果表明，采用基于PSO算法优化后的BP神经网络的热误差补偿方法大大提高了机床加工精度。

4 结束语

以GMC4000H/2 五坐标横梁移动龙门加工中心为对象，针对影响机床加工精度的热误差因素，提出了一种将粒子群算法与BP神经网络相结合进行机床热误差补偿的方法。在介绍热误差检测方法和热补偿系统的基础上，运用所检测到的实验数据，建立误差补偿模型，进行MATLAB仿真，验证方法的可行性。结果表明:该方法补偿精度高，网络学习收敛速度快，且补偿效果明显优于普通BP神经网络。

【1】傅建中，姚鑫骅，贺永，等.数控机床热误差补偿技术的发展状况[J].航空制造技术，2010(4):64－66.

【2】杜正春，杨建国，关贺，等.制造机床热误差研究现状与思考[J].制造业自动化，2002(10):1－3.

【3】孙勇，曾黄磷.一种新的数控机床热误差实时补偿方法[J].机械设计与制造，2010(1):244－245.

【4】高峰.PSO－BP组合人工神经网络算法研究[J].山西大同大学学报:自然科学版，2010(3):66－69.

【5】MATLAB 中文论坛.MATLAB神经网络30个案例分析[M].北京:北京航空航天大学出版社，2010:236－242.

【6】杜华英.基于PSO算法的BP神经网络研究[J].现代计算机，2009(2):28－29.

【7】HECHT－NIELSEN R.Kolmogorov＇s mapping neural network existence theorem[C]//IEEE First International Conference on Neural Networks，New York:[s.n.]，1987.

【8】李祚泳，汪嘉杨，郭淳.PSO算法优化BP网络的新方法及仿真实验[J].电子学报，2008(11):2224－2228.