高盒形件拉深计算及坯料展开方法

施于庆

(浙江科技学院 机械与汽车工程学院,杭州 310023)

高盒形件拉深计算及坯料展开方法

施于庆

(浙江科技学院 机械与汽车工程学院,杭州 310023)

由于高盒形件不能一次拉深成形,其初始坯料尺寸、中间工序尺寸比较难确定,这给成形模具的结构设计带来困难。对此,提出一种高盒形件拉深计算及坯料展开方法,将高盒形件4个圆角拼接成设想的杯形件,用杯形件拉深系数算法来确定高盒形件拉深次数及模具结构,从而提高了模具的设计精度和效率,并通过算例说明了该方法的有效性。

高盒形件;拉深计算;坯料展开;模具;应力分布

1 盒形件拉深时的应力分布

图1 盒形件拉深时的应力分布Fig.1 Stress distribution of box-shaped parts in deep drawing

图1是盒形件拉深时的应力分布。拉深时,盒形件圆角处的坯料往长或短直边的地方移动,从而使圆角处拉应力σ1与压应力σ3产生了不均匀分布。圆角部位的中位线处σ3和σ1是最大的,在盒形件整个拉深时达到σ1max和σ3max;直边的中位线上的σ1和σ3最小,在盒形件整个拉深时为σ1min和σ3min。如此,盒形件拉深时总是在圆角处发生堆积破裂。但如果把盒形件4个圆角假想成一个杯形件,与该杯形件拉深相比,圆角处平均的σ1和σ3比相应的杯件要小一些,因为盒形件拉深时,直边部位和圆角部位是相互联系在一起的整体,根据最小阻力定律,板料拉深时,材料会向阻力最小的方向移动。所以,直边材料往凹模模腔中移动的阻力较小,圆角部分有一部分材料跟随着被拉到直边去,这样,圆角部分的压应力减小,使得圆角处克服压应力的拉应力减小。由于圆角处一部分材料往直边移动过去,在圆角处剩下的参与拉深的材料就减少了,即在圆角处拉深到凹模模腔中变成杯形件(此处为1/4杯形件)的直壁的材料就相应减少,故受到的拉应力减小,这样就提高了杯形件底部圆角上方处板料的承载能力。与把拉深假想成一个杯形件相比,拉深盒形件在圆角处就不容易发生破裂。无论是高或低盒形件,与设想其4个圆角拼接成杯形件相比,都是拉深成杯形件要复杂一些，出现破裂的可能性更大。因此,设想的杯形件能够1次拉深成形,则盒形件也一定能够1次拉深成形。盒形件能够1次拉深成形,则一定能满足低盒形件要求,就可按图解法得到坯料形状与尺寸。

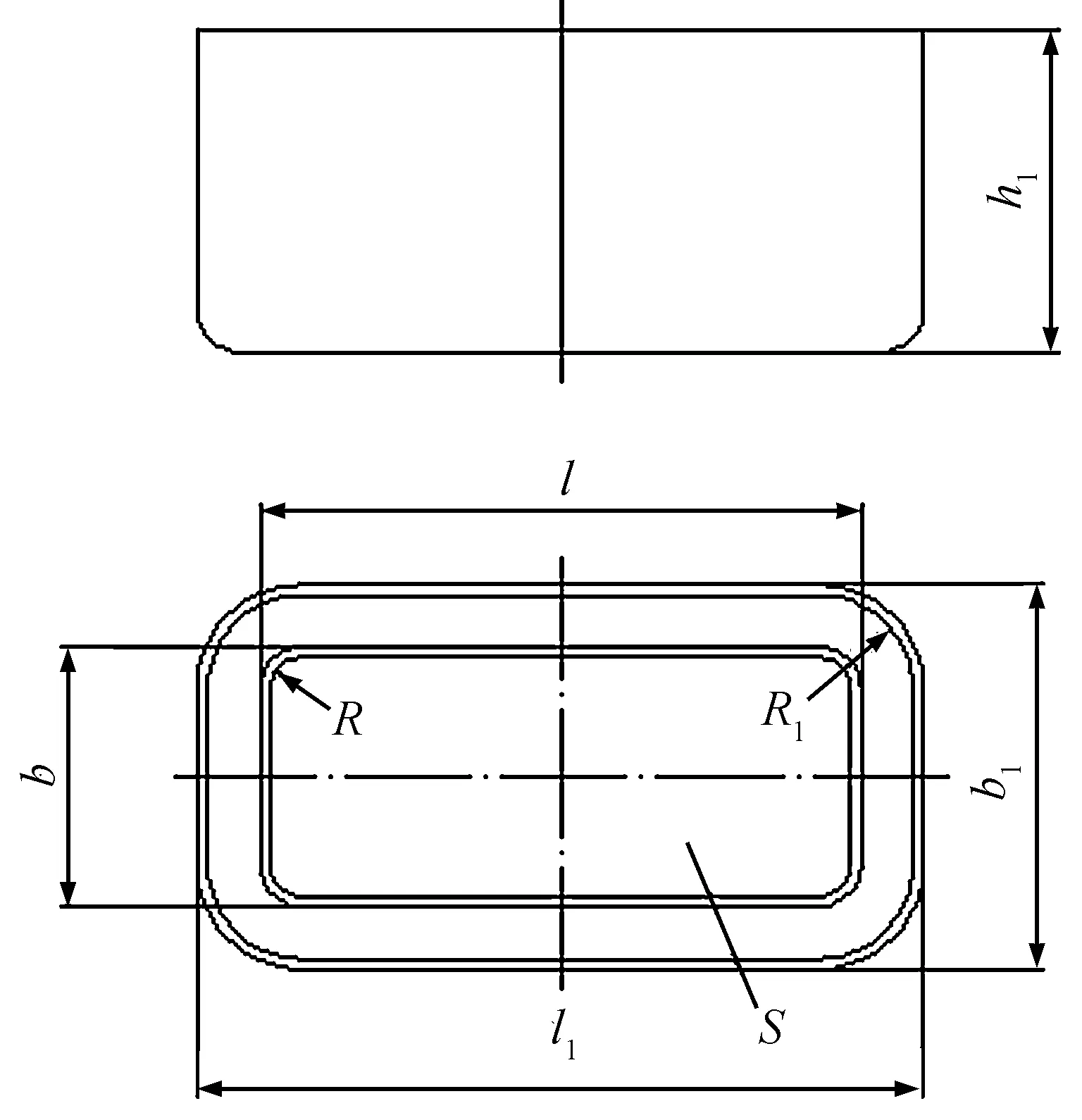
图2 盒形件Fig.2 Box-shaped parts

2 高盒形件拉深计算及坯料展开

设图2所示的盒形件为高盒形件，将其4个圆角设想为杯形件。杯形件的拉深系数计算式:

(1)

式(1)中:m为杯形件拉深系数;d为拉深后工件或半成品的直径;D0为拉深前坯料或半成品的直径。若m>m1min,则杯形件能1次拉深成功,m1min是被拉深板料的首次允许的极限拉深系数。若m=m1min,则杯形件拉深情况处于临界状态,即出现废品或拉深成功的可能性都有。若m

计算出圆板坯料直径，设为D0(图3)，将能首次拉成功的杯形件的直径设为d1,d1=D0×m1min,设盒形件4个角点的圆角半径为R1(图4),R1=d1/2。根据R1,相对应地就可求得首次可拉深成的盒形件长、宽、高分别为l1、b1、h1。

图3 假想的杯形件尺寸Fig.3 Dimension of the imagined cup-shaped parts

图4 盒形件形状对比Fig.4 Comparison of box-shaped parts in shape

由图4可得:l1=l+2(R1-R);b1=b+2(R1-R)。h1可由式(2)求得,根据拉深前后体积不变或表面积基本不变条件,有:

S=S1+S2=S1+(h1-t-r)×L1,

(2)

图5 首次能拉深盒形件各形状的面积Fig.5 Area of each shape for the box-shaped parts in first deep drawing

式(2)中:S为高盒形件表面积;S1为首次能拉深的盒形件底部表面积,见图5;S2为首次能拉深的盒形件高度部分表面积;t为料厚;r为盒形件直壁圆角半径,设每次拉深的r都相同;L1为首次能拉深的盒形件轮廓周长,L1=2(l1+b1)-8(t+R1)+πd1,则

(3)

用计算出的l1、b1、h1、R1、r来判断计算能否满足低盒形件要求。如果能1次拉深,则按图解法求出该盒形件坯料尺寸和形状。反之亦然,即用图解法得到的坯料形状和尺寸首次能拉深成尺寸为l1,b1,h1,R1,r的盒形件。以后各次拉深的盒形件4个角点的圆角半径仍可按杯形件直径计算得到,如此反复,直到R≥Rn,hn≥h,Rn为盒形件的4个角点的最小圆角半径,hn为盒形件最大拉深高度。

3 算 例

如果要完成盒形件拉深,则d2=0.75×71=53.25 mm,R1=26.6 mm;又由于R1=26.6 mm<30 mm,所以第1副模具拉深后的半成品件可在第2副模具中直接拉深成所要求的尺寸和形状的盒形件。表1是高盒形件计算前后的情况对比,可比较清楚地反映该方法的实用性。

表1 高盒形件计算前后的情况对比Table 1 Comparison of high box-shaped parts before and after calculation

4 结 语

根据经验估算法一般比较难确定高盒形件的原始坯料和中间工序形状及尺寸,给模具的结构设计带来了一定的困难。将盒形件4个角点拼接设想成杯形件,按照杯形件拉深系数的计算方法,求出盒形件首次可拉深的形状和尺寸,根据图解法反求得到原始坯料展开尺寸和形状,使高盒形件还原成低盒形件,计算方便,模具结构设计简化,从而提高了设计精度和效率。

[1] 施于庆.用相似原理计算盒形拉深件展开尺寸[J].杭州应用工程技术学院学报,2000,12(2):17.

[2] 施于庆.汽车制动阀安装板坯料形状与尺寸的确定[J].浙江科技学院学报,2015,27(3):186.

[3] 施于庆.冲压工艺及模具设计[M].杭州:浙江大学出版社,2012:178-179.

[4] 王秀凤,张永春.冷冲压模具设计与制造[M].北京:北京航空航天大学出版社,2012:127.

[5] 余年生.深盒形件液压拉深成形工艺研究[J].模具工业,2008,34(1):20.

[6] 郎利辉,许诺,王永铭,等.深腔类盒形件充液成形技术研究[J].锻压技术,2013,38(2):21.

[7] 李涛,郎利辉,安冬洋,等.复杂薄壁零件板多级充液成形及过程数值模拟[J].北京航空航天大学学报,2007,33(7):830.

[8] 刘合军,郎利辉,李涛,等.高强度铝合金板材的温热介质充液成形研究[J].塑性工程学报,2009,16(1):31.

[9] 胡志华,慕东.铝合金盒形件拉深的变压边力控制[J].热加工工艺,2013,42(3):84.

[10] 李琳,陈忠家,李奇,等.盒形件分区变压边力拉深研究[J].锻压技术,2016,41(2):25.

[11] 陈炜,周宏超,徐雪来,等.盒形件变压边力拉深成形研究[J].锻压技术,2014,39(11):20.

[12] 吴斌,单云.分块式压边圈盒形件成形数值模拟研究[J].锻压技术,2015,40(9):139.

[13] 李奇涵,王红强,刘海静,等.基于BP神经网络矩形盒件拉深成形变压边力的预测[J].锻压技术,2015,40(11):27.

[14] 罗昱,胡建华,陈昶,等.不同压边力加载模式对盒形件拉深成形的影响[J].锻压技术,2016,41(7):7.

[15] 张庆丰,金文中,周旭东.盒形件增量拉深成形数值模拟及工艺试验[J].锻压技术,2011,36(1):34.

Calculation of deep drawing in high box-shaped parts and blank unfolding method

SHI Yuqing
(School of Mechanical and Automotive Engineering, Zhejiang University of Science and Technology, Hangzhou 310023, Zhejiang, China)

The fact that the deep drawing process of high box-shaped parts can not be done all at a time poses challenges to structure design of the forming die for it is hard to determine the initial blank size and the intermediate process dimension. Accordingly, the article presents a method of deep drawing calculation and blank unfolding method, which joints four rounded corners of the high box-shaped parts to create an imagined cup. The deep drawing times and die structure can be figured out with the calculation method of deep drawing coefficient of the cup, which has improved design accuracy and efficiency of dies, and proved validity of the method through calculation examples.

high box-shaped parts; deep drawing calculation; blank unfolding; dies; stress distribution

10.3969/j.issn.1671-8798.2017.01.002

2017-01-12

施于庆(1959— ),男,浙江省杭州人,教授,硕士,主要从事板料成形研究。E-mail:syu163@163.com。

TG386.32

A

1671-8798(2017)01-0007-04