Com pton散射对1维3元未磁化等离子体光子晶体禁带影响
2013-03-10郝东山
郝东山
(郑州华信学院信息工程系,新郑451100)
Com pton散射对1维3元未磁化等离子体光子晶体禁带影响
郝东山
(郑州华信学院信息工程系,新郑451100)
为了研究Compton散射对1维3元未磁化等离子体光子晶体中TE波禁带影响,采用Compton散射模型和传输矩阵法,进行了理论分析和实验验证,取得了一些重要数据。结果表明,随着等离子体频率增大,左旋和右旋极化波禁带展宽比散射前减小0.09GHz,禁带主频率向高频区域移动增大0.48GHz。随着等离子体碰撞频率增大,两种极化波禁带宽度发生一定变化。随着等离子体回旋频率、填充率、光入射角和介质相对介电常数增大,左旋和右旋极化波禁带明显调谐效应。这一结果对等离子体光子晶体应用是有帮助的。
非线性光学;禁带;传输矩阵法;等离子体光子晶体
引 言
HOJO等人[1]曾提出等离子体光子晶体(plasma photonic crystals,PPC)概念,因其具有许多特性,如调节等离子体参量控制光子带隙[2]、外磁场使等离子体有各向异性等[3],成为人们研究热点[4-5]。按介质空间分布,可将PPC分为1维~3维。虽然2维、3维PPC比1维有较好特性[6],但是1维PPC易制备,对电磁波有禁带,故研究1维PPC更具现实意义。JOHN[7]和YABLONOVITCH[8]发现了光子禁带。SAKAI等人[9]指出,PPC透射波有类似光子晶子(photonic crystals,PC)带隙特性。ZHANG等人[10-11]指出,改变等离子体温度与密度可调控禁带。LI等人[12-13]指出,Compton散射对1维3元磁化PPC带隙有影响。但未涉及1维3元未磁化情况下的Compton散射。作者对此进行了探索。
1 理论分析
若等离子体中发生Compton散射[14](简称散射),散射光与入射光形成的耦合光频率为[13]:


式中,nc,e=ne+Δne为电子耦合密度,B和Bs,∥分别为入射光和散射光同向磁场强度。此外,εi(i= 1,2)和εp,Δεi和Δεp分别为介质A和B及等离子体D的介电系数及其相应增量。a和c,b分别为介质A和B厚度和等离子体厚度,如图1所示。

Fig.1 Physicsmodel
取ωp=7.9π×109rad/s,Δωp=108rad/s;νp= 1.9π×109rad/s,Δνp=π×108rad/s;ωb=11.9× 109rad/s,Δωb=108rad/s;ε1=13.8,Δε1=0.1,ε2=3.8,Δε2=0.1;a=5mm,b=9mm,c=7mm,周期α=20;θ=0°。模电场(transversal electric field,TE)和模磁场(transversalmagnetic field,TM)电场与B和Bs,∥垂直和平行,TE波形成左旋(left-handed circularly polarized,LCP)和右旋(right-handed circularly polarized,RCP)极化波。等离子体介电系数为:

式中,±分别对应LCP波和RCP波。耦合光可表示为[15]:


式中,nc,j=nj+Δnj,dj,θc,j=θj+Δθj及nj和Δni,θj和Δθj分别为j层介质耦合折射率、厚度、入射角及散射前折射率和入射角及其增量。推导应用了cosΔδj=cosΔθj=1,sinΔδj=0关系。经α个周期后,电、磁场、透射系数分别为:

式中,E(H)c,1=E(H)1+ΔE(H)1,Mc,A(D,B)= MA(D,B)+ΔMA(D,B),Mc,11(12)=M11(12)+ΔM11(12),Mc,21(22)=M21(22)+ΔM21(22),nc,0=n0+Δn0,E(H)c,(α+1)=E(H)α+1+ΔE(H)α+1。E(H)1和n0,ΔE(H)1和Δn0分别为散射前电场(磁场)、空气折射率及其相应增量。左旋和右旋极化波的透射频谱如图2所示,与参考文献[10]比较可知,位置未变的高频禁带变窄,低频禁带向高频移动。

Fig.2 Transmission spectum of LCP and RCP
2 数值模拟
2.1 等离子体频率对禁带影响
ωc,p=1GHz~25GHz的LCP和RCP透射频谱如图3所示。与参考文献[10]比较可知,随着ωc,p增大,两禁带展宽减小约0.1GHz,禁带频率向高频移动约增大0.45GHz。这是因为ωc,p越大,极化电子和等离子体吸收光越多,光衰减效应增大而减小了禁带拓展效应;ωc,p>>ω,光被截止;ω<10GHz,透射率峰值几乎减至为0。

Fig.3 Transmission spectrum whenωc,p=1GHz~25GHz
2.2 等离子体碰撞频率对禁带影响
νc,p=0.1GHz~85GHz的LCP和RCP透射频谱如图4所示。与参考文献[10]比较可知,随着νc,p增大,透射率峰值先迅速减小后再逐渐增大。这是因为νc,p增大,电子未完全极化与中性离子碰撞而降低吸收的缘故。

Fig.4 Transmission spectrum whenνc,p=0.1GHz~85GHz
2.3 等离子体回旋频率对禁带影响


Fig.5 Transmission spectrum whenωc,b=0.1GHz~40GHz
2.4 填充率、入射角和介电常数对禁带影响
填充率f=b/d=0.01~0.95的LCP和RCP透射频谱如6图所示。与参考文献[10]比较可知,禁带低频区展宽,透射率峰值减小直至消失。高频区新模式形成窄禁带数目增加,透射率峰值逐渐减小。

Fig.6 Transmission spectrum when f=0.01~0.95
入射角θ分别为0°~89°的LCP和RCP透射频谱如图7所示。与参考文献[10]比较知,ω<15GHz,禁带宽随θ增大而增大,透射率峰值逐渐减小;ω>15GHz,禁带宽随θ增大先减小后增大,透射率峰值逐渐减小。
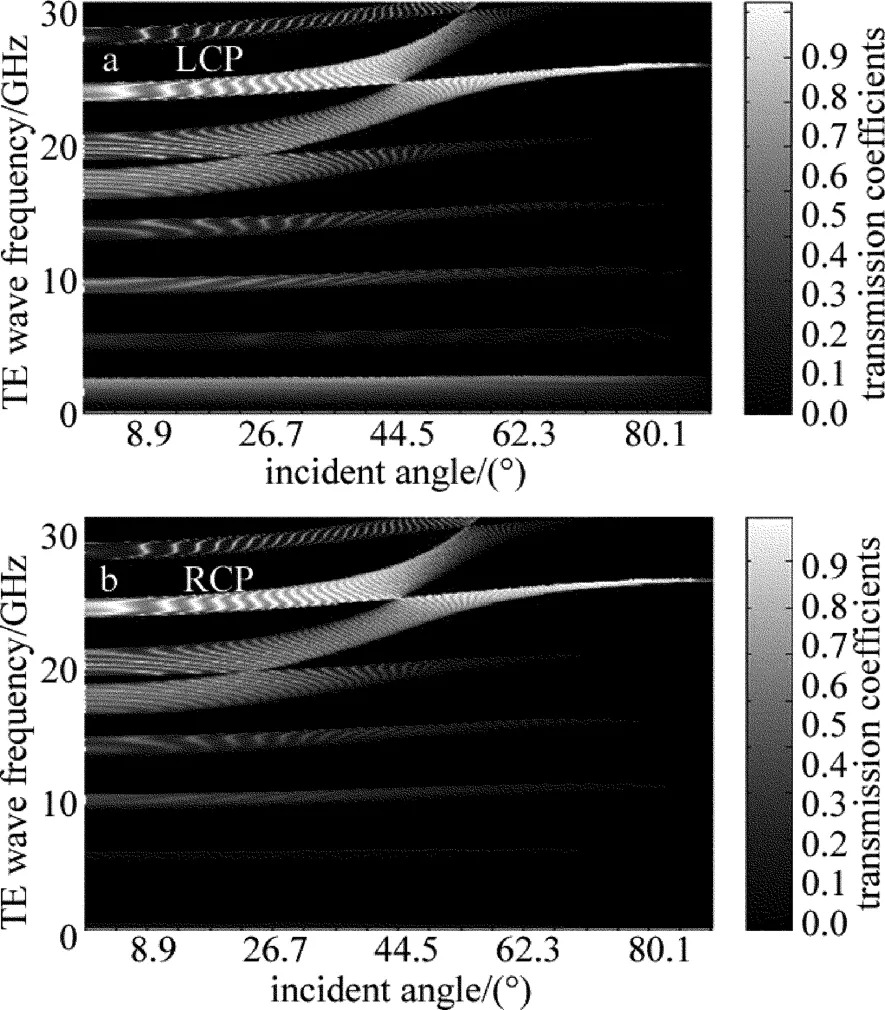
Fig.7 Transmission spectrum whenθ=0°~89°
介电常数比pc=εc,1/εc,2=0.26~6的LCP和RCP透射频谱如图8所示。与参考文献[10]比较可知,随着pc增大,两禁带宽(或数目)变宽(或增多),透射率峰值逐渐减小。这使得该PPC不引入缺陷即可实现多模滤波。

Fig.8 Transmission spectrum when pc=0.26~6
3 结 论
随着ωc,p增大,散射使LCP和RCP的禁带展宽减小0.09GHz,禁带中心频率向高频区域移动增大0.48GHz。随着νc,p,f,θ和pc增大,散射对两禁带宽有一定且明显的调谐作用。
[1]HOJO H,MASE A.Dispersion relation of electromagnetic wave in one-dimensional plasma photonic crystals[J].Journal of Plasma and Fusion,2004,80(2):89-92.
[2]LIU Sh B,ZHU Ch X,YUAN N Ch.FDTD simulation for plasma photonic crystals[J].Acta Physica Sinica,2005,54(6):2804-280(in Chinese).
[3]LIU Sh B,GU Ch G,ZHOU JH,et al.TDFD simulation formagnetized plasma photonic Crystals[J].Acta Physica Sinica,2006,55(3):1283-1288(in Chinese).
[4]ZHANGX J,WANG JZ.Effectof adiabatic dust charge fluctuation on three-dimensional solitary waves in inhomogeneous dusty plasmas[J].Acta Optica Sinica,2009,29(2):464-467(in Chinese).
[5]SHIJP,DONG K X,HUANG Y,et al.Second harmonic generation and effect factors in silica photonic crystalwaveguide[J].Acta Optica Sinica,2009,29(2):506-510(in Chinese).
[6]SAKAIO,TACHIBANA K.Properties of electromagnetic wave propagation emerging in 2-D periodic plasma structure[J].IEEE Transaction on Plasma Science,2007,35(5):1267-1272.
[7]JOHN S.Localization of photons in certain disordered dialectric superlattices[J].Physical Review Letters,1987,58(23):2486-2489.
[8]YABLONOVITCH E.Inhibited spontaneous emission in solidstate physics and electronics[J].Physics Review Letters,1987,58(23):2059-2063.
[9]SAKAI O,SAKAGUCHI T,TACHIBANA K.Verification of a plasma photonic crystal for microwaves of millimeter wavelength range using two dimensional array of columnarro-plasmas[J].Applied Physics Letters,2005,87(24):241505.
[10]ZHANG H F,MA L,LIU Sh B.Effects of plasma temperature and density to the characteristic ofband gap structure for un-magnetized plasma photonic crystals[J].Journal of Nanchang University(Natural Science Edition),2007,31(6):540-544(in Chinese).
[11]MIU G L,ZHANGH F,MA L.Temperature and density properties of prohibit band gaps for one dimension time-varying un-magnetized plasma photonic crystals[J].Journal of Nanchang University(Natural Science Edition),2010,34(1):66-74(in Chinese).
[12]LIF J,HAO D Sh.Influence of Compton scattering on the band gaps for one-dimensional ternary magnetized plasma photonic crystals[J].Laser&Infrared,2012,42(7):799-804(in Chinese).
[13]YU D Ch,HAO X F,HAOD Sh.Influence of filterwave of plasma photonic crystals with tunable defect produced by Compton scattering[J].Chinese Journal of Lasers,2011,38(10):1006001(in Chinese).
[14]KONG Q,ZHU L J,WANG JX,et al.Electron dynamics in the extra-intense stationary laser field[J].Acta Physica Sinica,1999,48(4):650-660(Chinese).
[15]WANG H,LIY P.Computation on band gap structure of photonic crystals using characteristic matrix means[J].Acta Physica Sinica,2001,50(11):2172-2178(in Chinese).
Effect of Com pton scattering on prohibited band gaps for 1-D ternary un-magnetized plasma photonic crystals
HAO Dong-shan
(Department of Information Engineering,Zhengzhou Huaxin University,Xinzheng 451100,China)
In order to study the effect of Compton scattering on TE wave prohibited band gaps of 1-D ternary unmagnetized plasma photonic crystals,based on themodel of Compton scattering and transfermatrix method,some important data was obtained after the theoretical analysis and experimental verification.The broadening width of prohibited band gap of the left circle polarization wave and the right circle polarization wave were decreased 0.09GHz along with the increasing of plasma frequency after Compton scattering.Themovement from the central frequency area of prohibited band gap to the high frequency areawas increased 0.48GHz.The change of prohibited band gapswidths of the left circle polarization wave and the right circle polarization wave happened along with the increasing of plasma collision frequency.The significant tuning effect of prohibited band gaps of the left circle polarization wave and the right circle polarization wavewas induced by Compton scattering along with the increasing of plasma circle frequency,filling index,light incident angle and relative dielectric constant.The result is helpful for the application of the plasma photonic crystals.
nonlinear optics;band gap;transfermatrixmethod;plasma photonic crystal
O437;O53
A
10.7510/jgjs.issn.1001-3806.2013.04.022
1001-3806(2013)04-0515-04
河南省基础与前沿技术研究基金资助项目(092300410227)
郝东山(1949-),男,教授,主要从事激光物理与光纤通信基础理论研究。
E-mail:haodongshan1948@126.com
2012-09-17;
2012-11-20
