八角格子色散补偿光纤

廖洲一，刘 敏，钱 燕，何丁丁，简 多

（重庆大学通信工程学院，重庆400044）

八角格子色散补偿光纤

廖洲一，刘 敏*，钱 燕，何丁丁，简 多

（重庆大学通信工程学院，重庆400044）

为了消除光纤通信系统中色散，采用各向异性完全匹配层和全矢量有限元方法，进行了理论分析和实验验证，设计了一种基于八角格子晶体的同轴双芯色散补偿光子晶体光纤；得到了该色散补偿光纤的传输特性如基模有效折射率、色散、损耗和非线性系数方面的数据，并分析了光纤波导色散与色散补偿光纤结构参量之间的关系。结果表明，所设计的光纤在200nm的负色散范围内，拥有负色散值（在波长为1.55μm处有最低负色散值-1500 ps/（nm·km）），同时在E+S+C波段有较低的限制损耗（小于3.3dB/km）；非线性效应也得到显著抑制。

光纤光学；光子晶体光纤；有限元法；色散

引 言

光子晶体光纤［1］（photonic crystal fibers，PCFs）是RUSSELL等人于1992年首次提出的一种新型光纤。它是由石英棒或石英毛细管排列拉制而成，在中心形成缺陷。在光纤信息传输系统中，色散是一个非常重要的参量，过高的色散值会令脉冲发生展宽而使信元产生误码，因此必须采取色散补偿技术来补偿。目前常用的色散补偿方法有啁啾光纤光栅补偿法、频谱反转补偿法、预啁啾补偿法和色散补偿光纤（dispersion compensation fiber，DCF）补偿法［2］。DCF由于其易安装、损耗小等优势，是当今色散补偿技术研究的热点。

用DCF进行色散补偿最早可以追溯到1999年，BIRKS［3］等人制作了一种横截面由规则空气孔组成的光子晶体色散补偿光纤，随后，基于双芯的负色散补偿光纤得到了广泛的研究［4］。在同轴双芯光纤中传输的是内纤芯的基模和外纤芯的超模，二者会在某一波长处发生耦合，这一波长叫相位匹配波长λp。当波长小于λp时，光集中在内纤芯传播，基模为内纤芯的基模；当波长大于λp时，光主要被限制在外纤芯传播，基模为外纤芯的超模。当波长在λp附近时，内纤芯和外纤芯模式发生耦合，光会突然从内纤芯转移到外纤芯去。这种传播现象导致光纤的基模在λp处发生转折，色散发生反常变化，从而导致负色散的产生。2005年，HUTTUNEN提出的DCF可以达到-55000ps/（nm·km）的色散值［5］，但由于芯区掺杂，所设计结构的中心并非真正的单模。2006年，YANG［6］等人第1次在1.52μm～1.58μm范围内实现了宽带色散补偿，色散值大约-400ps/（nm·km）的色散值，但是由于橘子状的内心不易制作且掺杂的中心比较小，给制作带来了极大的困难。近些年来，随着光子晶体光纤拉制技术的改进，研究人员根据需要设计了不同排列的DCF，如四边形、蜂窝形［7］、圆形［8］等，这些结构都显示了其各自的优越性。

然而以往所设计的DCF只是单纯地追求色散值或者结构的特殊性，而忽略了光纤的负色散范围或者制作工艺的难度。本文中设计的八角格子色散补偿光纤（octagonal dispersion compensation fiber，O-DCF）结构较简单，作者利用全矢量有限元法（finite element method，FEM）对其结构进行了相关的数值分析，给出了不同波长下，光纤内外纤芯中基模的有效折射率，光纤的波导色散、限制损耗及非线性系数，并分析了当光纤结构参量发生变化时，波导色散的变化。

1 数值分析方法

采用各向异性完全匹配层［9］（perfectly matched boundary layers，PML）吸收边界条件和FEM［10］来分析O-DCF的结构。运用这种方法，仅仅需要设置光纤的几何结构和电磁参量，便可以计算出光纤在任意波长下的基模有效折射率neff和模场分布情况。基模的有效折射率包括实部（Re［neff］）和虚部（Im［neff］）。利用基模有效模折射率的实部，就可以相应计算出光纤的色散；利用其虚部可以计算出光纤的限制损耗。

1.1 波导色散

光纤的总色散包括波导色散［11］和材料色散，由于一旦材料选定，材料色散就定了，材料对于光纤的影响是固定的，在此本文中忽略材料色散只考虑光纤的波导色散。波导色散D（λ）可以通过有效折射率的实部（Re［neff］）由下式得出：

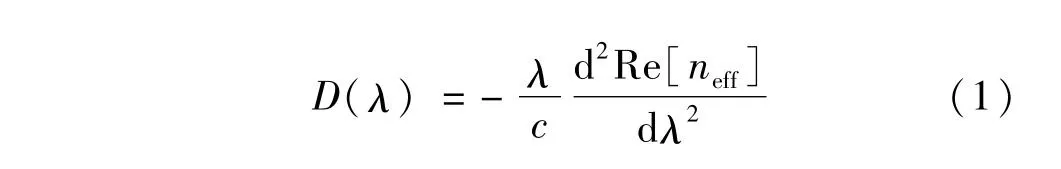
式中，c为真空中的光速，λ为波长。

1.2 限制损耗

限制损耗［12］Lc表征了光被限制在纤芯的能力，可以通过有效折射率的虚部（Im［neff］）得出：

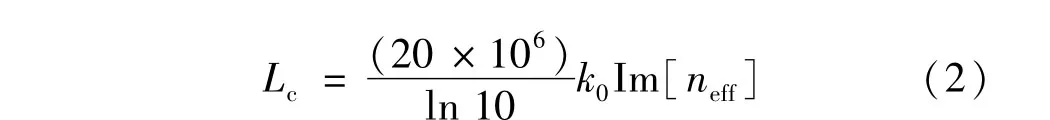
式中，k0=2π/λ为自由空间波数。

1.3 非线性系数

光纤的非线性系数γ［13］是一个很重要的参量，在光纤传输中，为了使信号受到的影响比较小，希望非线性系数比较小。非线性系数可以通过下式计算出：

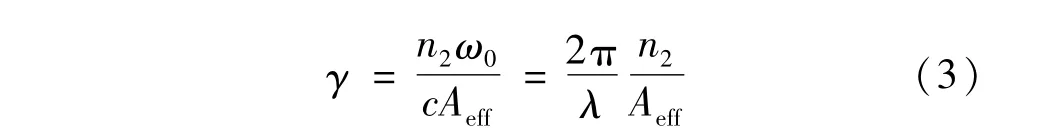
式中，n2=2.76×10-20m2/W2，ω0为角频率，Aeff是光纤基模的有效模场面积，可以由下式计算出：

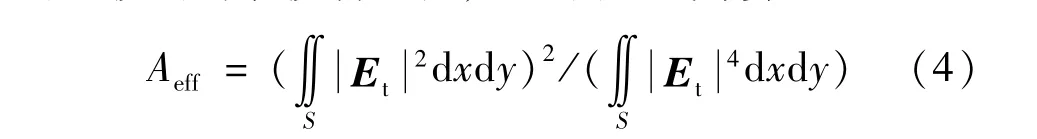
式中，Et为横电场矢量，S为光纤的横截面。

2 理论模型

O-DCF的横截面如图1所示，背景为SiO2材料，包层呈八角格子分布，包含3种直径不同的空气孔。d1，d2，d3分别表示3种空气孔的直径，且大小关系满足d1＞d3＞d2，Λ表示空气孔的周期距离。去掉结构中心的空气孔形成缺陷从而构成O-DCF内纤芯，直径为d1的空气孔作为内纤芯的包层，为了使内外纤芯充分的隔离，采用直径比较大的空气孔作为内纤芯的包层。直径为d2的空气孔形成了O-DCF的外纤芯（见图1的虚线标注）。由于d2最小，这层的有效折射率得到了相对的提高，从而增加了内外纤芯的折射率差，达到了实现负色散的条件。第3层以外的空气孔为外纤芯的包层，直径为d3。这种同轴双芯光纤结构仅通过改变空气孔直径的大小来达到改变内外纤芯折射率差的目的，以实现负色散，并没有掺入高折射率物体，这在很大程度上减少了实际制作的困难，也消除了高阶模的影响。由于光纤结构的对称性，为了减少仿真时间，本文中只仿真了光纤的1/4结构。在O-DCF中，内纤芯传输的是单模，外纤芯传输的是超模。经过计算发现，当Λ=2.0μm，d1=1.40μm，d2=0.54μm和d3= 1.20μm时，在波长为1.55μm处具有最低负色散，且负色散范围为1.45μm～1.65μm。基于这组参量，本文中分析了光纤的色散随结构参量变化的情形。

Fig.1 Cross-section of the designed O-PCF

3 数值模拟结果与分析

3.1 基模

图2a描述了O-DCF内外芯基模的有效折射率以及模场分布图随波长的变化，图2b描述了O-DCF波导色散随波长的变化曲线。图2a中实线为ODCF内纤芯的基模，点线是外纤芯的基模，二者随着波长的增加呈单调递减的趋势。从图2中可以看出，内纤芯和外纤芯基模有效折射率曲线在λp= 1.55μm处发生交叉，相位达到匹配，λp即相位匹配波长。当λ＜λp时，内纤芯和外纤芯基模有效折射率大于外纤芯的有效折射率，光主要被限制在内纤芯中，光纤的基模主要是内纤芯的基模；在λ=λp时，光会从内纤芯转移到外纤芯中，从而内外芯之间发生耦合，产生负色散（-1500ps/（nm·km），见图2b）；当λ＞λp时，外纤芯基模的有效折射率大于内纤芯基模的有效折射率，光主要被限制在外芯中，光纤的基模主要是外纤芯的基模。图2表明，所设计的O-DCF在1.45μm～1.65μm的范围内有负色散的产生，在1.55μm处负色散最小值为-1500ps/（nm·km）。

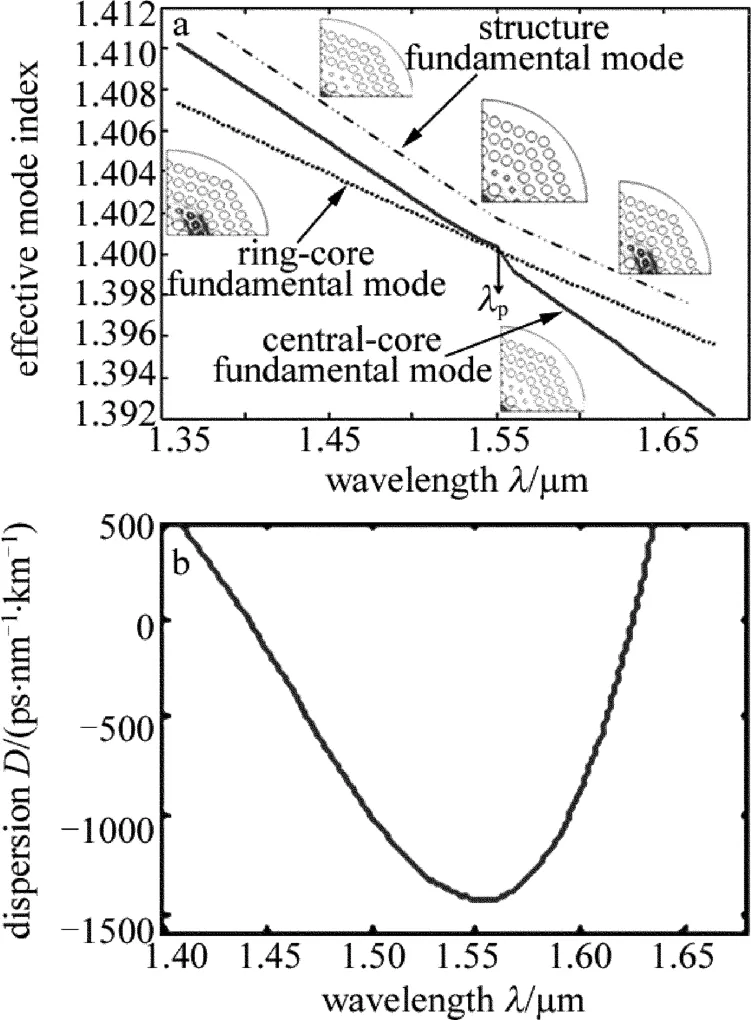
Fig.2 Effective index and chromatic dispersion versus wavelengtha—effective index versus wavelength b—chromatic dispersion versus wavelength

3.2 波导色散

图3为包层中3种空气孔的直径d1=1.4μm，d2=0.54μm和d3=1.2μm条件下，以d2组成的外纤芯从第2层变化至第4层时，光纤色散的变化曲线图，内纤芯的包层空气孔的直径全部为d1= 1.4μm。图中的N表示以d2组成的外纤芯在包层中的位置。从图中可以看出，随着外纤芯向外层移动即外纤芯和内纤芯距离的增加，负色散峰值点向短波长漂移，而曲线的形状并没有发生大的改变，可见内外纤芯距离的改变对色散的影响比较小。

Fig.3 Chromatic dispersion values as the ring-core in variant air layers

图4为在保持空气孔周期距离Λ和空气孔直径d3，d2一定条件下，空气孔直径d1从1.32μm以步径0.08μm变化到1.48μm时，波导色散随d1变化的色散曲线图。从图中可以看出，在其它参量未发生变化时，增加d1会使O-DCF的负色散的峰值向短波长移动，同时峰值增加。然而负色散范围却随着峰值的增加而减少。可见色散的峰值和光纤的负色散范围呈反比关系，要得到宽的负色散范围，需要牺牲负色散值。

Fig.4 Chromatic dispersion values versus d1variation

从图5中可以看出，当不改变其它结构参量，增加空气孔直径d2，对光纤的负色散峰值点向长波长漂移而曲线形状并没有明显的改变。可见d2对负色散的峰值的大小影响较小，但是却可以影响峰值的移动。

图6为在空气孔间距Λ和空气孔直径d1，d2一定的情况下，色散随空气孔直径d3变化曲线。从图中可以看出，在保持空气孔间距Λ和空气孔直径d1，d2的条件下，d3的增加会使O-DCF的负色散的峰值向长波长移动，同时负色散范围增加。但是同时带来了色散值的降低。可见调节外纤芯空气孔的大小可以很好地调节色散值的大小。

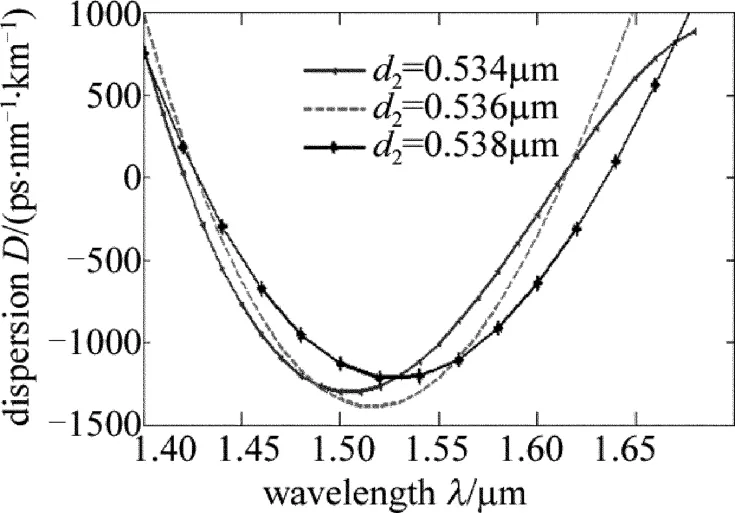
Fig.5 Chromatic dispersion values versus d2variation

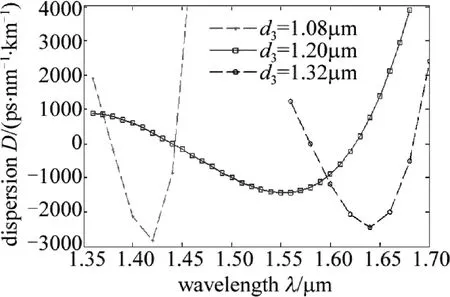
Fig.6 Chromatic dispersion values versus d3variation

.3 限制损耗特性

O-DCF的限制损耗由（2）式计算出，绘制成的曲线见图7。从图中可以看出，当波长小于1.55μm时，限制损耗非常低，不超过0.5dB/km，光被很好地限制在内纤芯中。在波长等于1.55μm处，由于场分布从内纤芯移至外纤芯，内外纤芯发生耦合，使限制损耗在相位转折波长处发生突变，而大于此波长，基模为外纤芯的基模，限制损耗比内纤芯大，但也不高于3dB/km。由于所设计的色散补偿光纤分为内纤芯和外纤芯，并且内外纤芯是独立传输的，内纤芯有内纤芯的基模折射率，外纤芯有外纤芯的基模折射率，只是在小于1.55μm处光主要在内纤芯传输，光纤的基模折射率为内纤芯的基模折射率，大于1.55μm的波长光纤的基模主要是外纤芯基模。由于同轴双芯光纤传输的是泄露模，而泄露模的耦合情况可以用内外纤芯的限制损耗来表征。内纤芯的折射率的虚部比外纤芯的折射率虚部小，导致在小于1.55μm时，外纤芯的限制损耗曲线在内纤芯的限制损耗曲线的上部；在1.55μm处，光从内纤芯转移到外纤芯，二者发生耦合，二者的折射率相同，虚部也相同，限制损耗相同，内外纤芯的限制损耗曲线相交；大于1.55μm的波长，两纤芯继续保持自己的限制损耗变化规律，这时候光主要在外纤芯传播，光纤的限制损耗为外纤芯的限制损耗。所以在1.55μm的地方会发生突变。

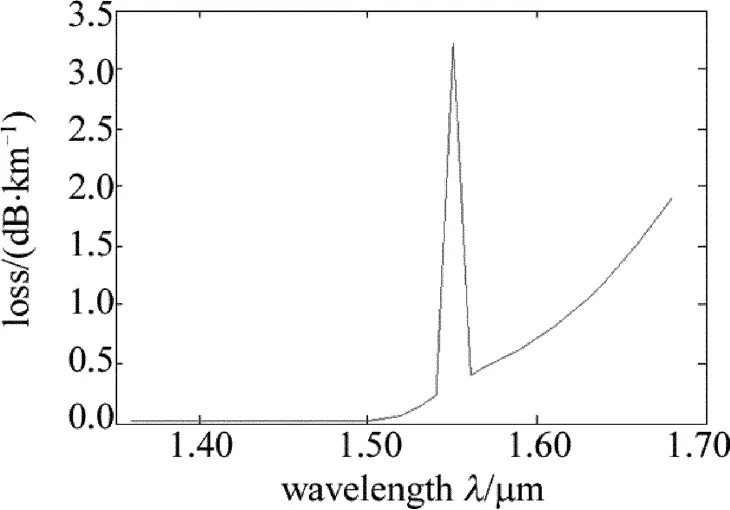
Fig.7 Confinement loss as a function of wavelength

3.4 非线性系数

光纤的非线性系数是一个很重要的参量，在光纤传输中，为了使信号不失真，希望非线性系数越小越好。通过（4）式计算出O-DCF在1.55μm处的基模的有效模场面积为49.5μm2，较以往的结果有了很大的提升。利用（3）式计算出在不同波长处的非线性系数，如图8所示。从图中可以看出，非线性系数在1.55μm处发生突变，由20（W·km）-1降到2.55（W·km）-1。发生突变的原因是在1.55μm处，内外纤芯发生了耦合，导致基模模场面积增加。本文中的结果与参考文献［12］中的相比，有了显著提升。

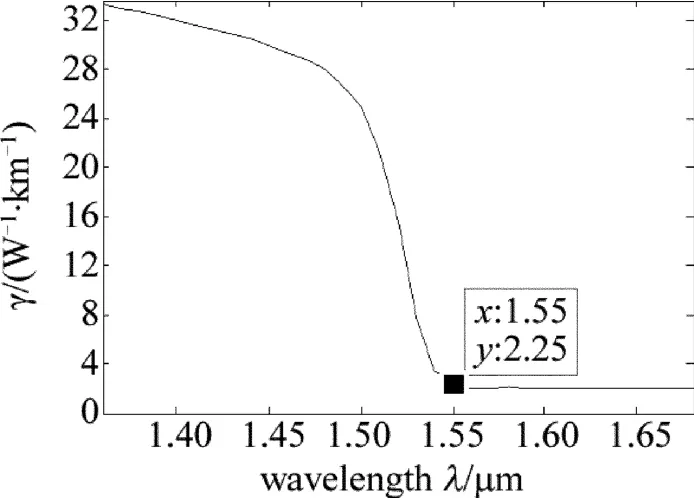
Fig.8 Nonlinear coefficientwith wavelength

4 小 结

设计了一种八角格子色散补偿光纤，运用FEM和PML方法对其性能进行了分析，分析发现，在中心没有掺杂的情形下，此O-DCF在1.55μm处有大的负色散值，达-1500ps/（nm·km），负色散范围为1.45μm～1.65μm，达200nm。同时在E+S+C波段限制损耗低于3.3dB/km，非线性效应也得到显著抑制。与以往所设计的八角格子晶体相比，在负色散值、负色散范围、限制损耗和非线性系数方面有明显的提高。同时，要想实现不同的色散值和范围，只需要控制空气孔的大小。鉴于以上优点，这种八角格子色散补偿光纤可以用于光纤通信系统中。

［1］ZHANG M，LIU M，SUN SH，et al.Analysis of temperature sensing characteristics of photonic bandgap photonic crystal fiber［J］.Laser Technology，2012，36（2）：204-207（in Chinese）.

［2］WANG H H，WANG S J.Analysis of negative dispersion properties of a photonic crystal fiber with modified square lattice and double concentric cores［J］.Acta Sinica Quantum Optica，2009，15（4）：368-373（in Chinese）.

［3］BIRKS T A，MOGILEVTSEV D，KNIGHT JC，et al.Dispersion compensation using single-material fibers［J］.IEEE Photonics Technology Letters，1999，11（6）：674-676.

［4］WANG H H，XUEW R，ZHANGW M.Negative dispersion properties of photonic crystal fiber with dual core and compositelattice［J］.Acta Optica Sinica，2008，28（1）：27-30（in Chinese）.

［5］HUTTUNEN A，TORMA P.Optimization of dual-core and microstructure compensation and largemode area［J］.Optics Express，2005，13（2）：627-635.

［6］YANG SG，ZHANG Y J，HE L N.Broadband dispersion-compensating photonic crystal fiber［J］.Optics Letters，2006，31（19）：2830-2832.

［7］TAN X L，GENG Y F，TIAN Z，et al.Study of ultra-flattened dispersion squre-lattice photonic crystal fiber with low confinement loss［J］.Optoelectronics Letters，2007，15（2）：124-127.

［8］LI J，ZHANG W G，DU J B，et al.Application of hydrofluoric acid’s corrosive properties in the fabrication of photonic crystal al fibers［J］.Chinese Journal of Lasers，2009，36（3）：705-709（in Chinese）.

［9］FUJISAWA T，SAITOH K，WADA K，et al.Chromatic dispersion profile optimization of dual-concentric-core photonic crystal fibers for broadband dispersion compensation［J］.Optics Express，2006，14（2）：893-900.

［10］SONG D J，XIE K，XIAO J.Mode field and dispersion analysis of photonic crystal fiber based on finite elementmethod［J］.Laser Technology，2012，36（1）：111-117（in Chinese）.

［11］HE F L，LIU M，DONG Ch P，etal.Rearch of dispersion characteristics of squre-lattice all solid photonic bandgap fibers［J］.Laser Technology，2012，36（1）：90-92（in Chinese）.

［12］HOU S L，HAN JW，ZHU P，et al.Low nonlinear optical fiber broadband dispersion compensation design based on double core photonic crystal fiber［J］.Chinese Journal of Luminescence，2010，31（3）：449-452（in Chinese）.

［13］CHEN J，GEW P，WANG XW.Design of a novel octagonal photonic crystal fiber with flat dispersion and high nonliearity［J］.Laser Technology，2012，36（4）：481-484（in Chinese）.

Octagonal dispersion com pensation fiber

LIAO Zhou-yi，LIU Min，QIAN Yan，HE Ding-ding，JIAN Duo
（College of Communications Engineering，Chongqing University，Chongqing 400044，China）

In order to eliminate dispersion in a fiber communication system，based on the finite elementmethod and perfectly matched boundary layers，an octagonal dispersion compensation fiberwas proposed.The guiding properties such as fundamentalmode，dispersion，confinement loss and nonlinear coefficient were obtained.Besides，it was shown that the negative dispersion over 200nm bandwidth was obtained（theminimum value was-1500ps/（nm·km）atλ=1.55μm）.Meanwhile，the fiber exhibited low confinement loss less than 3.3dB/km at1.55μm in the entire E+S+C band.Also，the nonlinear effectwas eliminated effectively because of the low nonlinear coefficient.

fiber optics；photonics crystal fiber；finite elementmethod；dispersion

TN929.11

A

10.7510/jgjs.issn.1001-3806.2013.04.020

1001-3806（2013）04-0506-05

国家自然科学基金资助项目（61007049）

廖洲一（1986-），女，硕士研究生，主要从事光子晶体光纤领域的研究。

*通讯联系人。E-mail：liumin＠cqu.edu.cn

2012-09-05；

2012-11-08