一种激光二极管像散光束准直整形方法研究
2013-03-28谢洪波吕二阳祝晓晨姚丽娟
谢洪波,吕二阳,祝晓晨,李 勇,姚丽娟
(天津大学精密仪器与光电子工程学院光电信息工程系,天津300072)
一种激光二极管像散光束准直整形方法研究
谢洪波,吕二阳,祝晓晨,李 勇,姚丽娟
(天津大学精密仪器与光电子工程学院光电信息工程系,天津300072)
为了准直并整形具有像散的激光二极管光束,采用高斯光束q参量变换规律,推导了利用柱面自聚焦透镜整形激光二极管光束应满足的条件,并在此基础上,通过软件模拟优化,得到了一套效果良好的光束整形准直系统。经过准直整形后光束快慢轴方向发散角基本相等,均小于0.7mrad,束腰位置差异小于2.8mm。结果表明,系统中柱面自聚焦透镜的应用起到了较好的效果,准直整形后的光束具有发散角较小且旋转对称等特点。
激光器;准直整形;柱面系统;自聚焦透镜
引 言
激光二极管(laser diode,LD)具有工作性能稳定、结构简单、体积小、发光效率高、单色性好等优点。在光通讯、激光加工、精密测量及激光投影显示中有着广泛的应用前景[1]。但是由于非对称激活通道使其出射光束的发散角较大且存在像散,一般情况下,快轴方向的发散角在30°~60°之间,慢轴方向的发散角在10°~30°之间,这种非对称性严重制约了激光二极管的使用,因此,需要对其出射光束进行准直整形。
目前,国内外对LD光束进行准直整形的主要方式有:(1)柱透镜系统。分别对LD快轴和慢轴两个方向进行准直和整形,整个结构复杂,体积较大;(2)衍射元件系统。结构简单,效果较好,但衍射元件加工难度大,且衍射效率较低;(3)变形梯度折射率系统。结构简单,易于封装在微结构中,但是由于工作距离和材料本身尺寸的限制,无法达到较好的准直效果[2-5]。
作者针对LD光束特性,运用近轴变换矩阵推导了柱面自聚焦透镜整形LD光束应满足的条件,并在理论分析的基础上使用CODE V软件设计了一套光束准直整形系统。
1 光束整形原理
高斯光束经自聚焦透镜传播后,仍然保持高斯光场分布。对于快慢轴方向发光面尺寸差异比较小的激光二极管,两个方向束腰均位于发光面处,但是由于束腰尺寸不一致,即存在横向像散,经过旋转对称光学系统后,出射光束的束腰位置及其大小不相等,成为具有像散的高斯光束,因此,需要非对称的光学系统对LD出射光束进行整形[4,6]。柱面自聚焦透镜整形LD光束,是在自聚焦透镜的基础上,将透镜端面改为柱面形式,构造非对称光学系统。通过改变前后端面面形,使LD光束经柱面自聚焦透镜后,快慢轴方向的光束截面半径在不同的传播距离处均相等,实现光束整形的目的。
在距离发光面d处光束光场分布可以用以下公式进行描述[2]:
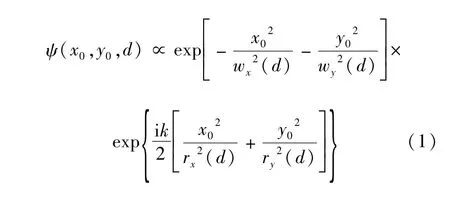
式中,d为光束在空间中传播的距离,wx(d)和wy(d)分别为距离发光面d处快慢轴方向光束截面半径,rx(d)和ry(d)分别为距离发光面d处对应x,y方向光束波前曲率半径。
自聚焦透镜折射率分布公式为:
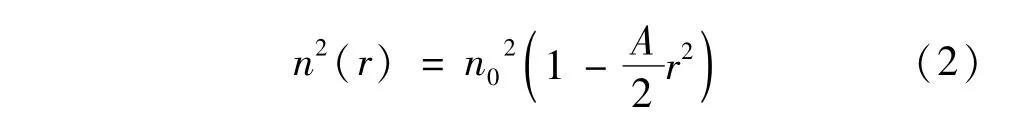
式中,r为端面半径。当透镜端面为平面时,r→∞[7-8]。在近轴条件下,光束在自聚焦透镜内的传输矩阵可以表示为:

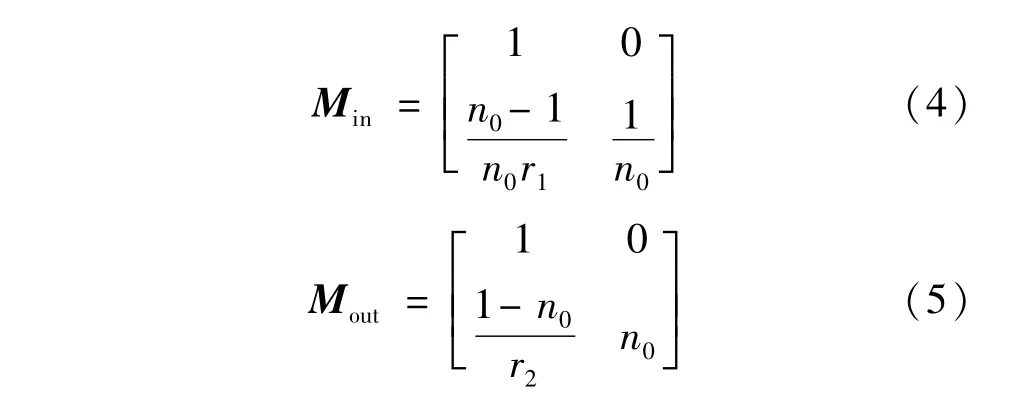
式中,n0是透镜中心折射率,是聚焦常数,z为透镜长度,r1为光由空气传输到自聚焦透镜时端面曲率半径,r2为光由自聚焦透镜传输到空气时透镜端面曲率半径。
对于前后端面为柱面自聚焦透镜,其传输矩阵为:

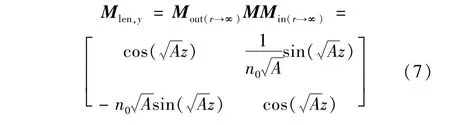
光束在空间中传播距离d的传输矩阵为:
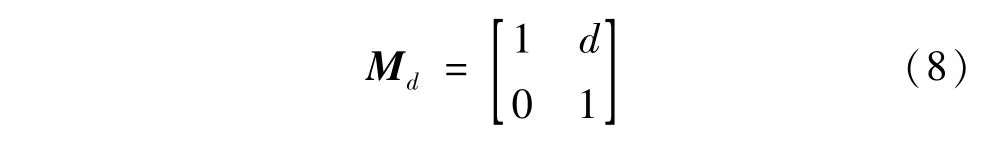
光束在空间中传播d1后,进入柱面自聚焦透镜,在距离透镜后端面d2处的传输矩阵可以表示为:
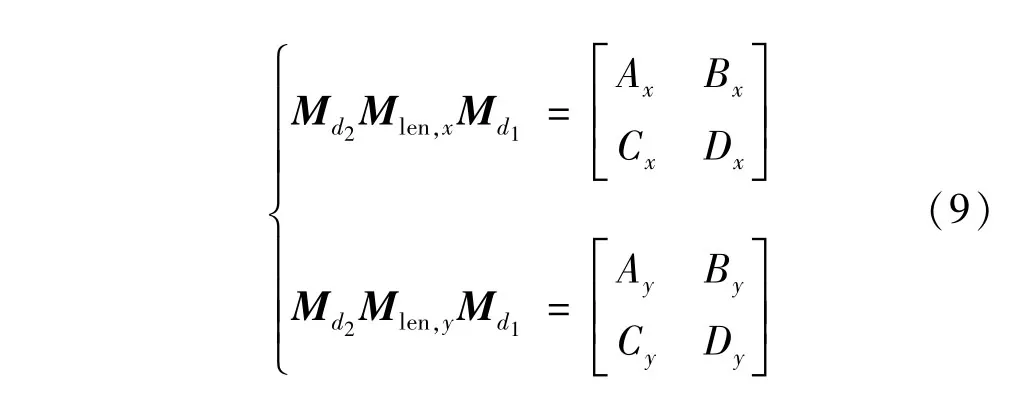
式中,A,B,C,D为矩阵元,根据高斯光束传输规律,LD光束经过快慢轴方向相异的传输矩阵后得到对应方向的参量q,再通过求取虚部,即可得到同一个截面上快慢轴方向的光斑尺寸:
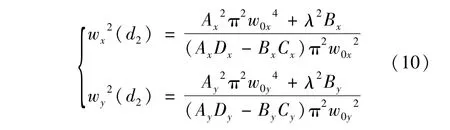
式中,λ是波长,w0x,w0y为LD光束快慢轴方向束腰半径,wx(d2),wy(d2)为经过近轴变换矩阵后LD光束在距离透镜后端面d2处的光束截面半径。

2 软件模拟LD光束在自聚焦透镜中的传播
若要在LD光束整形的基础上同时实现对光束进行准直,则需要单独讨论w0x,w0y,d1,z,λ,自聚焦透镜的参量及n0等参量对LD光束的影响。因为变量较多,彼此之间的关系较为复杂,故将变量逐一数值化,仅保留变量z,通过CODEV软件模拟自聚焦透镜长度z对光束的影响。
下面以三菱公司的ML520G54型红色激光二极管为例进行分析。激光光束中心波长638nm,发光区域4μm×2μm,θFWHM=9°×19°,快慢轴方向束腰位于发光面处。
依据高斯光束发散角与束腰之间变换公式:
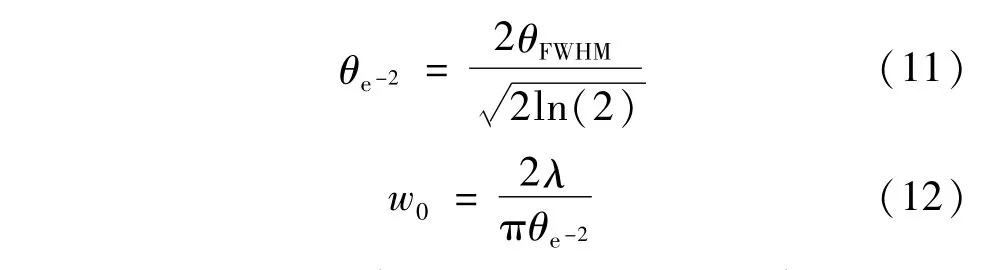
式中,θe-2为LD光束远场发散角,w0为束腰半径,θFWHM为激光光束的半峰全宽角。
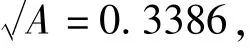
使用CODEV软件模拟激光二极管光束在自聚焦透镜中传播,不改变透镜端面面形,仅改变透镜长度,记录光束快慢轴方向发散角和束腰位置差异的变化情况,将模拟的结果进行参量拟合,如图1和图2所示。
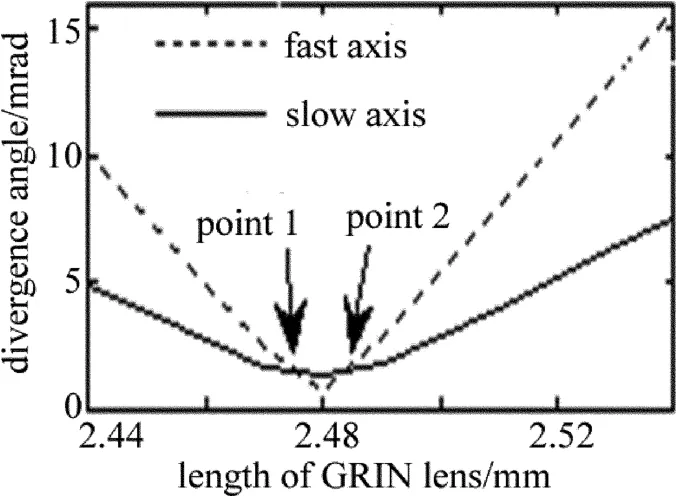
Fig.1 VariationofdivergenceanglesalongwiththechangeofGRIN’length

Fig.2 VariationofastigmatismalongwiththechangeofGRIN’length
由图1可知,由于LD快慢轴方向束腰尺寸不同,经自聚焦透镜准直后的光束在对应方向上发散角不同。透镜长度变化的过程中,快慢轴方向发散角变化曲线存在两个交点,交点处表示两个方向发散角相等,此时传播像散大约为-700mm。由图2可知,当准直后的光束发散角都较大时,像散较小,当发散角较小时,透镜长度微小量变化会引起像散出现较大的波动。图中曲线与坐标系横轴存在一个交点,交点处像散值为0,此时慢轴方向的发散角是快轴方向的2倍,没有实现快慢轴同时准直的目的。
通过以上分析可知,若仅以自聚焦透镜长度为变量,无法同时达到光束整形和准直的目的。因此引入端面面形为变量,在准直的基础上对光束进行整形。
3 消像散准直系统设计

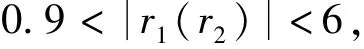
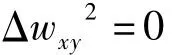
在宽光束条件下使用CODEV软件进行优化设计,首先确定自聚焦透镜长度为2.48mm,其次将自聚焦透镜端面改为柱面形式,其母线与激光二极管出射光束的快轴方向平行。考虑到实际应用情况,透镜前表面应该为凸面,依据理论分析,只有当柱面镜前后端面半径同号的时候存在解,则后表面应该为凹面。理论计算与软件设置中符号法则存在差异,对应于图3b解空间,将自聚焦透镜前后端面半径赋初始值均为1,并更改其属性为变量进行优化。
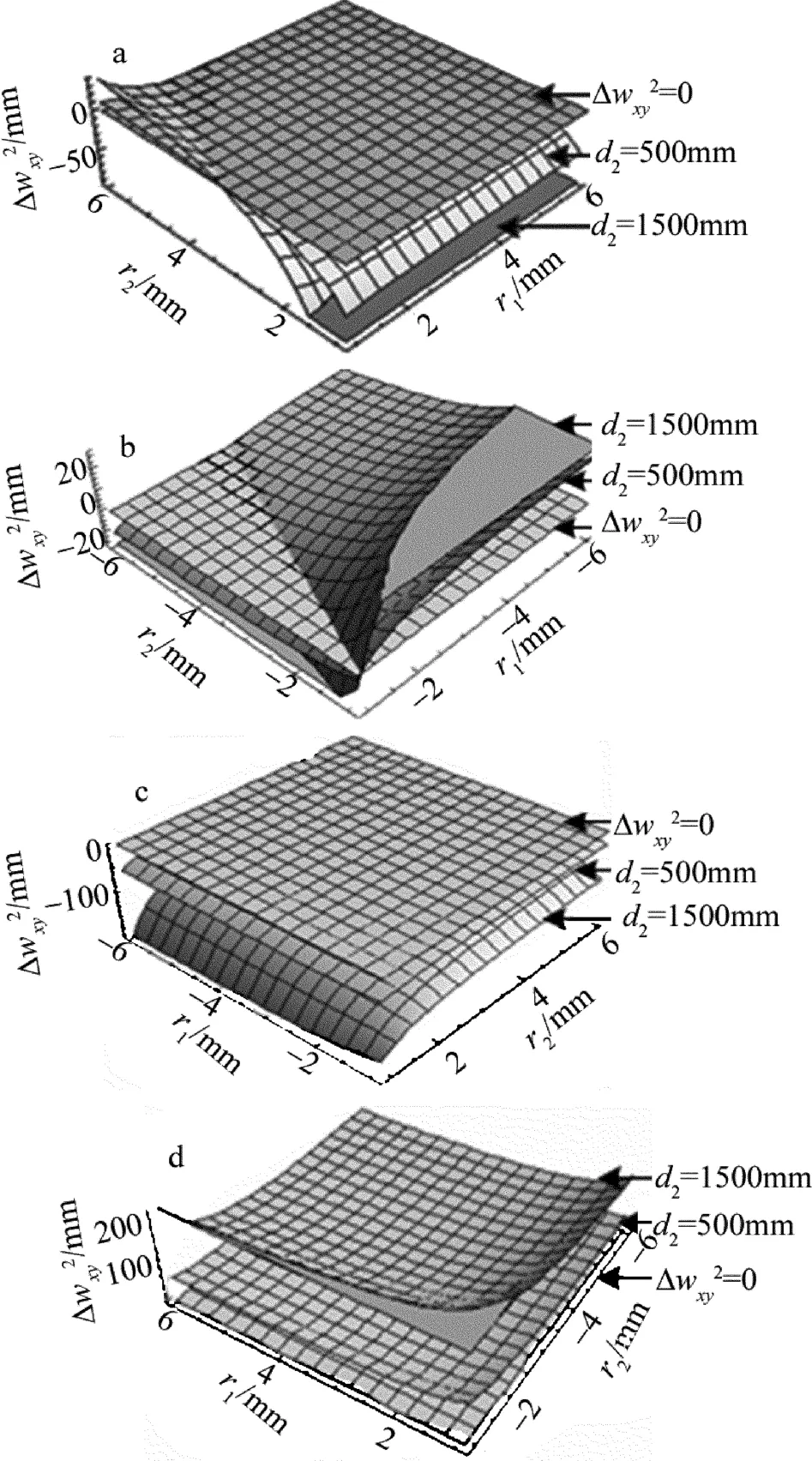
Fig.3 Function graphics in different definition domains
经CODE V软件的优化,对应于LD光束快轴方向,柱面自聚焦透透镜前后端面的半径分别为1.053mm和1.117mm,准直整形后光束快慢轴方向束腰半径基本相同,差异在0.3%以内,远场发散角约1.23mrad,快慢轴方向束腰位置差异值小于10mm。光束在空间中从500mm传播到1500mm时,光束截面为圆形。
一般应用中需要更小的发散角,可以在柱面自聚焦透镜准直整形LD光束的基础上,附加一个球面单透镜进行2级准直[9-10],见图4。
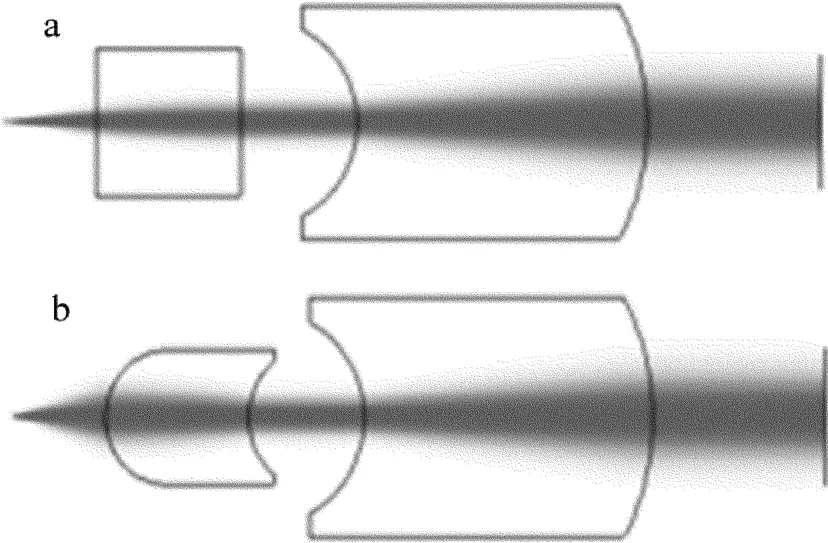
Fig.4 a—schematic diagram of collimating the beam in slow axis b—schematic diagram of collimating the beam in fast axis
通过附加一个球面单透镜,对整形准直后的LD光束进行了2次准直,得到了更小的光束发散角,整形准直后光束快慢轴方向发散角为0.69mrad左右,两方向束腰位置差异小于2.8mm,达到了同时准直整形光束的目的。
由于柱面自聚焦透镜承担了主要的准直及其整形功能,所以对其加工精度要求比较高。自聚焦透镜厚度公差在±0.01mm、半径公差在±0.001mm范围内时,可以通过调节光学元件之间的间隔,保持良好的光束准直整形效果。
由于自聚焦透镜直径较小,可能引起比较严重的衍射效应。当高斯光束通过圆形孔径时,若a为通光孔径,w为传播截面上光场振幅减少到的光斑半径。当>1.5时,有99%以上的能量通过,可以忽略衍射效应[7]。经过优化设计后的系统,光束在自聚焦透镜上光场振幅减少到的最大截面半径为0.465mm,自聚焦透镜半径为0.9mm,对应> 1.8,因此可以忽略远场衍射效应。
应用本文中的方法,同样也可以对激光二极管组进行光束准直整形,但是由于其特殊的光源结构,需要使用微型化的自聚焦透镜阵列,在较短的工作距离处才能满足使用条件。
4 结 论
推导了柱面自聚焦透镜整形LD光束应满足的条件,并以此为基础应用软件模拟优化了一套能够对LD出射光束进行准直整形的光学系统。系统结构简单、体积小,相比于LD出射光束,经过该光学系统变换后的光束具有发散角小、旋转对称的特点。
[1]CHELLAPPANKV,ERDENE,UREYH.Laser-baseddisplays:areview[J].AppliedOptics,2010,49(25):79-98.
[2]ACOSTAE,GONZALEZRM,GOMEZ-RAINOC.Designofan anamorphicgradient-indexlenstocorrectastigmatismofGaussian laserbeams[J].OpticsLetters,1991,16(9):627-629.
[3]CHENG,ZHAOChM,JIRY,etal.SimulationdesignofsemiconductorlasercollimationbasedonZEMAX[J].LaserTechnology,2012,36(3):318-321(inChinese).
[4]SINZINGERS,BRENNERHH,MOISELJ,etal.Astigmatic gradien-tindexelementsforlaser-diodecollimationandbeamshaping[J].AppliedOptics,1995,34(29):6626-6632.
[5]GAOYH,ANZhY,LINN,etal,OpticaldesignofGaussian beamshaping[J].OpticsandPrecisionEngineering,2011,19(7):1464-1471.
[6]XUQ,ZENGXD,ANYY.Propagationoflaserdiodesbeam throughagradientindexlens[J].ActaPhotonicaSinica,2007,36(s1):72-74(inChinese).
[7]LIXJ,YAOJQ,ZHANGBG.AnalysesonpropagationandimagingpropertiesofGRINlens[J].SPIE,2002,4919:155-160.
[8]ZHOUBK,GAOYZh,CHENJY,etal.Laserprinciples[M].Beijing:NationalDefenseIndustryPress,2009:70-83(inChinese).
[9]SMITHWJ.Modernopticalengineering[M].4thed.Beijing:ChemicalIndustryPress,2011:260-264(inChinese).
[10]ZHENGP,YANGYP,TAOY,etal.Designoftwo-levellaser beamexpanderbasedonGalileanstructure[J].JournalofAppliedOptics,2008,29(3):347-350(inChinese).
Shaping and collimation of LD beam w ith astigmatism
XIE Hong-bo,LÜEr-yang,ZHU Xiao-chen,LIYong,YAO Li-juan
(Department of Photoelectric Information Engineering,College of Precision Instrument and Opto-electronics Engineering,Tianjin University,Tianjin 300072,China)
In order to collimate and shape the LD beam with astigmatism,the mathematic condition for LD beam shaping with a cylindrical gradient-index lenswas introduced applying ABCD law.Based on this,a system with good effect was got through software simulation.After collimation and beam shaping,the beam in fast and slow axis has the same divergence angle which is less than 0.7mrad and the beam waist difference in z axis is less than 2.8mm.The result shows a good effectwas obtained with a cylindrical gradient-index lens in this system.Under the condition of beam shaping and collimation,the LD beam has the characteristics of small divergence angle and rotationally symmetry.
lasers;collimation and shaping;cylindrical system;gradient-index lens
TN248.4
A
10.7510/jgjs.issn.1001-3806.2013.04.030
1001-3806(2013)04-0551-05
谢洪波(1969-),男,博士,副教授,主要从事光学成像与显示技术主面的研究。
E-mail:hbxie@tju.edu.cn
2012-08-27;
2012-11-05
