石墨烯光栅太赫兹透射特性的研究
2015-03-23李彤彤曹妍妍吕欢欢黄晓燕徐世林张会云张玉萍
李彤彤,曹妍妍,吕欢欢,黄晓燕,张 晓,徐世林,张会云,张玉萍
(山东科技大学电子通信与物理学院,青岛市太赫兹技术重点实验室,山东青岛266590
1 引言
石墨烯(graphene)是由碳原子紧密堆积成的单层二维蜂窝状物质,是构建其他维度碳质材料的基本结构单元[1],是目前世界上最薄的材料。由于其优异的物理特性、光电特性和磁学特性,石墨烯引起了人们的广泛关注。石墨烯的室温量子霍尔效应[2]、铁磁性[3]和零载流子浓度极限下的最小量子电导率等特性,使其可应用于各种领域,成为科学领域的一个研究热点[4-5]。
目前对石墨烯带的研究已有很多报道[6-9]。周期排列的石墨烯带(石墨烯光栅)是一种特殊的光栅。当太赫兹波入射时,会与石墨烯光栅的表面等离激元极化波产生共振作用,因而出现透射增强现象。通过调节石墨烯光栅各项参数,可应用于各种领域,如可调谐太赫兹滤波器和等离子体波导等。采用多种方法对石墨烯光栅的透射增强现象进行研究,其中,傅里叶模方法简单高效,成为最常用的一种方法。若不能选择恰当的傅里叶分解,TM偏振波入射时收敛性较差,为此,Amin Khavasi提出了一种近似边界条件[10],使收敛速度得到了较大提高。目前对石墨烯带的研究主要集中于表面等离子体的激发和传输特性,对石墨烯光栅的透射特性的研究较少。
基于以上研究背景,本文建立了石墨烯光栅模型,基于快速收敛傅里叶模方法对石墨烯光栅的太赫兹透射特性进行了理论研究,讨论了费米能级、光栅周期、光栅占空比和弛豫时间对透射率的影响,为石墨烯光栅的研究提供了有力指导。
2 模型及理论基础
如图1(a)所示为石墨烯光栅结构整体视图,图1(b)所示为石墨烯光栅结构的横截面图,灰色长条为石墨烯带,其宽度为W,排列周期为L,在y方向无限延伸,占空比为W/L。石墨烯光栅上下两种介质的介电常数分别为ε1=3ε0和ε2=4ε0。入射角为θ的TM偏振的平面波(磁场沿y轴正方向)射向石墨烯光栅。
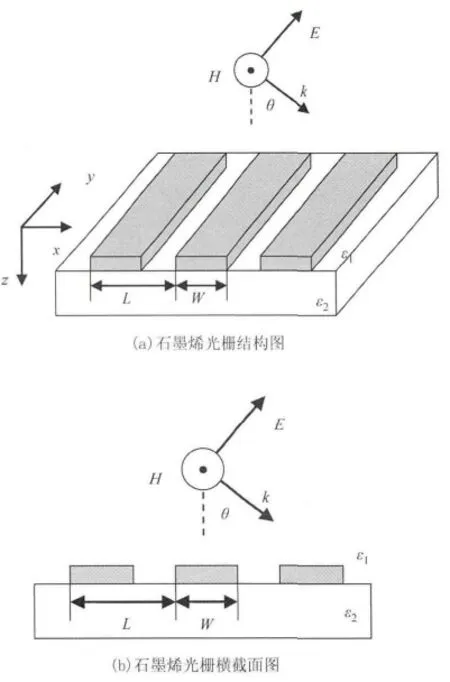
图1 石墨烯光栅结构模型示意图Fig.1 Schematics of the graphene gratings
石墨烯的表面电导率可表示为[11]:

其中,e是电子电荷量;EF是费米能级;是约化普朗克常量;ω是频率;τ是弛豫时间;H是赫维赛德函数[12],有如下定义:
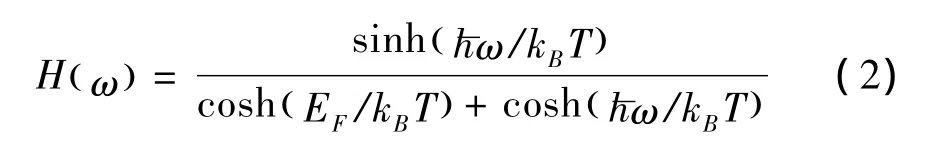
在石墨烯光栅中,将磁场瑞利展开为如下形式:
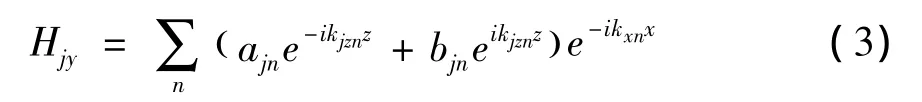
由石墨烯带分布的区域分界处的边界条件可得:
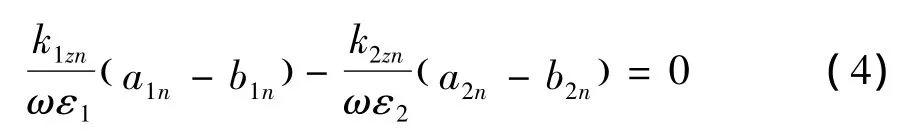
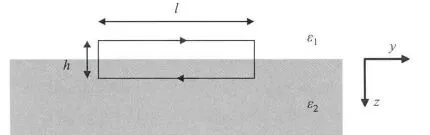
图2 求解近似边界条件所需的长方形闭合回路,高为h,长为lFig.2 Rectangular closed loop of length l and height h used for solving the approximate boundary condition
在z=0处,将石墨烯电导率的表达式作傅里叶展开,得到:
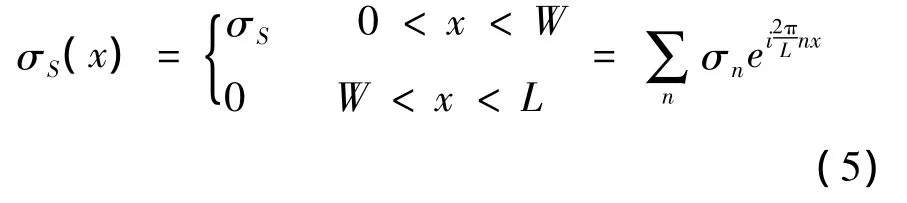
如图2所示为一个闭合回路结构,长度为l,高为h。由安培环路定理可得到:



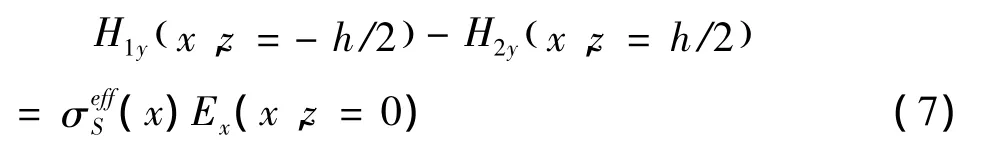
经计算可得到:
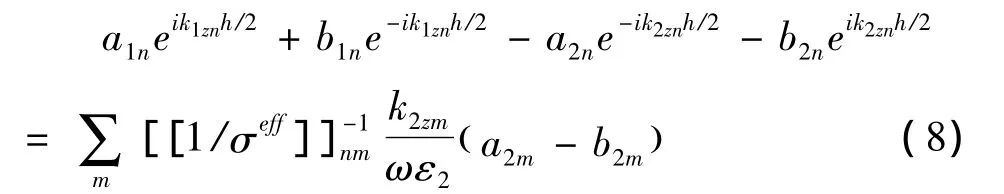
其中,[[σ]]代表托普利兹矩阵;第(n,m)个元素为 σn-m。
将式(4)和式(8)联立,用 S矩阵形式[13]表示为:
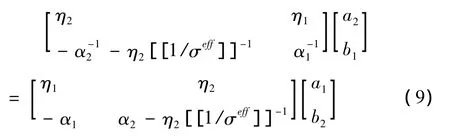
其中,ηj为对角矩阵,其对角元素为kjzn/ωεj。
由式(9)可以得出透射系数a2,进而可以求出透射率[10]为:
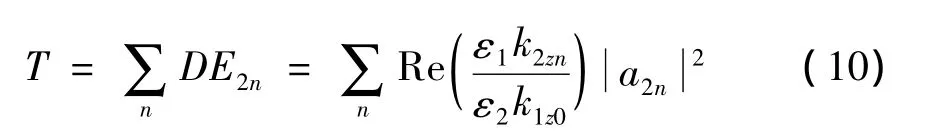
3 结果分析和讨论
图3所示为正入射条件下,费米能级取不同值时透射率与入射光频率的关系曲线。从图中可以看出,当费米能级取一固定值时,透射率随入射光频率的增加先减小后增大。当费米能级取不同值时,在入射光频率较高的条件下,透射率随费米能级的增大而减小;在入射光频率较低的条件下,透射率随费米能级的增大而增大。透射率最小值随费米能级的增大向高频移动,且数值逐渐减小。此图表明,在高频附近区域,适当减小费米能级有助于提高石墨烯光栅透射率;在低频附近区域,则适当增大费米能级有助于提高其透射率。
图4所示为正入射条件下,光栅周期取不同值时透射率与入射光频率的关系曲线。从图中可以看出,当入射光频率较高时,透射率随光栅周期的增大而增大;当入射光频率较低时,透射率随光栅周期的增大而减小。透射率最小值随光栅周期的增加向低频移动。此图表明,在高频附近区域,适当增大光栅周期有助于提高石墨烯光栅透射率;在低频附近区域,则适当减小费米能级有助于提高其透射率。

图3 正入射的条件下,费米能级取不同值时,透射率与频率的关系曲线Fig.3 Transmission versus frequency at four different Fermi levels for normal incidence

图4 正入射的条件下,光栅周期取不同值时,透射率与频率的关系曲线Fig.4 Transmission versus frequency at four different periods of grating for normal incidence
图5所示为正入射条件下,光栅占空比取不同值时透射率与入射光频率的关系曲线。从图中可以看出,当光栅占空比取一固定数值时,透射率随入射光频率的增加先减小后增大。当光栅占空比取不同值时,透射率随光栅占空比的增大而减小;透射率最小值随光栅占空比的增大向低频移动,且数值逐渐减小。此图表明,适当减小光栅占空比有助于提高石墨烯光栅透射率。
图6所示为正入射条件下,弛豫时间取不同值时透射率与入射光频率的关系曲线。从图中可以看出,当弛豫时间取一固定值时,透射率随入射光频率的增加先减小后增大。当弛豫时间取不同值时,在入射光频率为3.79 THz的条件下透射率取得最小值,且透射率最小值随弛豫时间的减小而增大。

图5 正入射的条件下,光栅占空比取不同值时,透射率与频率的关系曲线Fig.5 Transmission versus frequency at four different duty cycles of grating for normal incidence

图6 正入射的条件下,弛豫时间取不同值时,透射率与频率的关系曲线Fig.6 Transmission versus frequency at four different relaxation times for normal incidence
通过以上结果分析,可以得出:在正入射条件下,石墨烯费米能级为0.8 eV、光栅周期为6 μm、占空比为0.4、弛豫时间为1 ps时,透射率在1 THz处达到最佳。
图7所示为入射光频率为2 THz的条件下,费米能级取不同值时透射率与入射角的关系曲线。从图中可以看出,当费米能级取一固定值时,透射率随入射角的增大先增加后减小;当费米能级取不同值时,透射率随费米能级的增大而增大。当入射角约为60°时,透射率取得最大值,且透射率峰值随费米能级的增加而增大。此图表明,适当增大费米能级有助于提高石墨烯光栅的透射率。
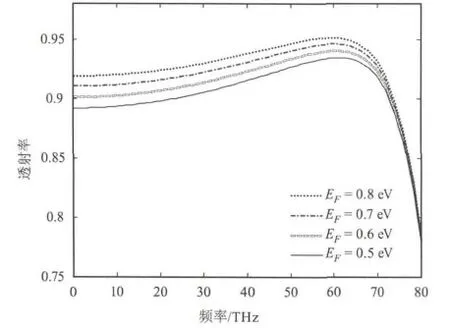
图7 入射光频率为2THz的条件下,费米能级取不同值时,透射率与入射角的关系曲线Fig.7 Transmission versus incident angle at four different Fermi levels when incident frequency is fixed to 2 THz
图8所示为入射光频率为2 THz的条件下,光栅周期取不同值时透射率与入射角的关系曲线。从图中可以看出,当光栅周期取一固定值时,透射率随入射角的增大先增加后减小;当光栅周期取不同值时,透射率随光栅周期的增大而减小;透射率峰值随光栅周期的增加而减小。此图表明,适当减小光栅周期有助于提高石墨烯光栅的透射率。
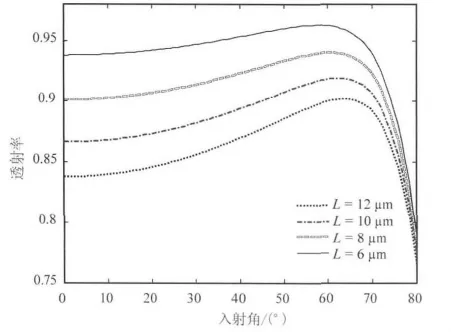
图8 入射光频率为2 THz的条件下,光栅周期取不同值时,透射率与入射角的关系曲线Fig.8 Transmission versus incident angle at four different periods of grating when incident frequency is fixed to 2 THz
图9所示为入射光频率为2 THz的条件下,光栅占空比取不同值时透射率与入射角的关系曲线。从图中可以看出,当光栅占空比取一固定值时,透射率随入射角的增大先增加后减小;当光栅占空比取不同值时,透射率随着光栅占空比的增大而减小;透射率峰值随光栅占空比的增大而减小。此图表明,适当减小光栅占空比有助于提高石墨烯光栅的透射率。

图9 入射光频率为2 THz的条件下,光栅占空比取不同值时,透射率与入射角的关系曲线Fig.9 Transmission versus incident angle at four different duty cycles of grating when incident frequency is fixed to 2 THz
图10所示为入射光频率为2 THz的条件下,弛豫时间取不同值时透射率与入射角的关系曲线。从图中可以看出,当弛豫时间取一固定值时,透射率随入射角的增大先增加后减小;当弛豫时间取不同值时,透射率随弛豫时间的增大而增大;透射率峰值随弛豫时间的增大而增大。此图表明,适当增大弛豫时间有助于提高石墨烯光栅的透射率。
通过以上结果分析,可以得出:在入射光频率为2 THz条件下,石墨烯费米能级为0.8 eV、光栅周期为6 μm、占空比为0.4、弛豫时间为 1 ps时,透射率在入射角约为60°处达到最佳。
为了更好地研究石墨烯光栅透射率与入射角和频率的关系,做出弛豫时间为0.25 ps,占空比为0.5,周期为8 μm,费米能级为0.6 eV 时,透射率随入射角和频率变化的三维关系图,如图11所示。从图中可以看出,当入射光频率不变时,透射率随入射角的增大先增加后减小,并在入射角约为60°附近取得峰值;当入射角不变时,透射率随频率的增大先减小后增加,并在入射光频率约为3.79 THz处取得最小值。
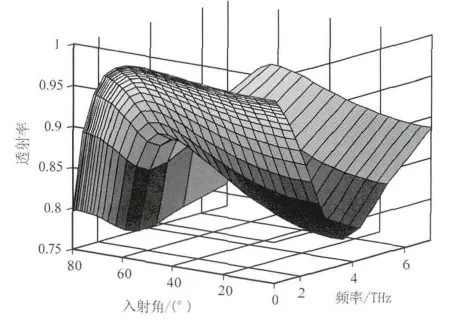
图11 透射率、入射角和波长的三维关系图Fig.11 Transmission spectra versus frequency and incident angle
4 结论
本文建立了石墨烯光栅模型,基于快速收敛傅里叶模方法对石墨烯光栅的太赫兹透射特性进行了理论研究,讨论了不同费米能级、光栅周期、光栅占空比和弛豫时间对透射率的影响。研究结果表明,在正入射条件下,透射率随频率的增大先减小后增加,且费米能级、占空比和弛豫时间越高,透射率最小值越小。在入射光频率为2 THz的条件下,透射率随入射角的增大先增加后减小,随费米能级、弛豫时间的增大而增加,随光栅周期、光栅占空比的增大而减小,且透射率在入射角约为60°时取得最大值。通过以上研究,可以根据实际应用调节石墨烯光栅参数,从而达到最佳透射效果,为石墨烯滤波器等器件的制作提供理论指导。
[1] Geim A K,Novoselov K S.The rise of graphene[J].Nature materials,2007,6(3):183-191.
[2] Novoselov K S,Jiang Z,Zhang Y,et al.Room-temperature quantum Hall effect in graphene[J].Science,2007,315(5817):1379.
[3] Nomura K,MacDonald A H.Quantum Hall ferromagnetism in graphene[J].Physical Review Letters,2006,96(25):256602.
[4] Hao Qiulai,Zhou liqing.Synthesis and optical-electrical charaertistics of graphene[J].Laser & Infrared,2014,44(12):1295-1300.(in Chinese)郝秋来,周立庆.石墨烯合成及其光电特性[J].激光与红外,2014,44(12):1295-1300.
[5] Song Haoqing,Yang Aiying.Reserach progress of graphene passively mode-locked fiber lasers[J].Laser &Infrared,2013,43(2):137-143.(in Chinese)宋浩青,杨爱英.石墨烯被动锁模光纤激光器的研究进展[J].激光与红外,2013,43(2):137-143.
[6] Wu J,Zhou C,Yu J,et al.Design of infrared surface plasmon resonance sensors based on graphene ribbon arrays[J].Optics & Laser Technology,2014,59:99-103.
[7] Gómez-Díaz J S,Esquius-Morote M,Perruisseau-Carrier J.Plane wave excitation-detection of non-resonant plasmons along finite-width graphene strips[J].Optics express,2013,21(21):24856-24872.
[8] Balaban M V,Shapoval O V,Nosich A I.THz wave scattering by a graphene strip and a disk in the free space:integral equation analysis and surface plasmon resonances[J].Journal of Optics,2013,15(11):114007.
[9] Chu H S,Gan C H.Active plasmonic switching at mid-infrared wavelengths with graphene ribbon arrays[J].Applied Physics Letters,2013,102(23):231107.
[10] Khavasi A.Fast convergent Fourier modal method for the analysis of periodic arrays of graphene ribbons[J].Optics letters,2013,38(16):3009-3012.
[11] Wunsch B,Stauber T,Sols F,et al.Dynamical polarization of graphene at finite doping[J].New Journal of Physics,2006,8(12):318.
[12] Thongrattanasiri S,Koppens F H L,de Abajo F J G.Complete optical absorption in periodically patterned graphene[J].Physical Review Letters,2012,108(4):047401.
[13] Koppens F H L,Chang D E,Garcia de Abajo F J.Graphene plasmonics:a platform for strong light-matter interactions[J].Nano Letters,2011,11(8):3370-3377.
[14] Li L.Formulation and comparison of two recursive matrix algorithms for modeling layered diffraction gratings[J].JOSA A,1996,13(5):1024-1035.
