基于互信息的并行约简＊

闫电勋， 邓大勇， 金皓苹， 陈 林

(浙江师范大学数理与信息工程学院，浙江金华 321004)

0 引言

为了在动态变化或增长的数据中求得一个稳定的约简结果，Bazan［1-2］提出了动态约简的概念．该理论的主体思想是先把要处理的决策表划分成若干个具有强烈概率因素的子表，然后求出全部子表的所有约简并取其交集．通常认为利用这种方式求得的约简结果较为稳定．然而，动态约简有2个缺点:一是必须求出全部子决策表的所有约简，时间复杂度很高;二是动态约简得到的结果有可能为空，理论本身不完备．

邓大勇在文献［3-6］中借鉴动态约简的分表思想提出了并行约简理论．并行约简和动态约简类似，都是将一个决策表拓展成若干个子表，然后在这些子表上求约简．和动态约简相比，并行约简算法有2个优点:一是在计算过程中可以利用启发式信息判断条件属性的优劣，不需要计算子表的全部约简，所以并行约简算法的时间复杂度是多项式级的;二是并行约简是一个完备的理论，它在定义层面就已经避免了约简结果为空这种情况的出现．

邓大勇［5］提出的并行约简概念和相应算法都是基于代数论知识的，因此可以称为代数意义下的并行约简(简称代数并行约简)．本文将提出信息论意义下的并行约简(简称信息论并行约简)概念及其相应的算法，信息论并行约简算法和代数论并行约简算法具有相同的时间复杂度，但在处理不一致数据时，信息论并行约简可以保留比代数并行约简更多的信息．

1 基础知识

本文假设读者熟悉粗糙集基本知识，因此对一些简单概念不再详细说明，只介绍与本文密切相关的知识．

1．1 动态约简

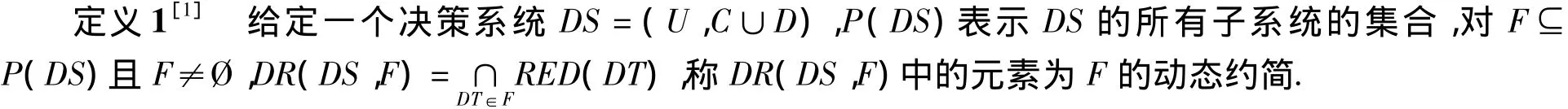
从定义1可以看出，如果想要求出动态约简，就必须首先求出F中全部子表的所有约简，这已经被证明是一个NP完全问题，其时间复杂度随着条件属性个数的增加呈指数级增长．而且动态约简得到的最终结果有可能是个空集，虽然Bazan等在文献［2］中试图解决动态约简的空集问题，但是如何决定参数ε又成了一个新的问题．

1．2 代数意义下的并行约简

为了在保证约简结果稳定性基础上解决动态约简NP难题和约简为空的问题，邓大勇［5］提出了代数并行约简的概念及其相应算法．代数并行约简同动态约简类似，也是把一个决策系统拓展成若干个子决策表，不同的是，代数并行约简并不需要求出全部子表的所有约简，而是只要找到一个能保证所有子表正域不变的约简即可［5］．

定义2［5］给定一个决策系统DS=(U，C∪D)，P(DS)表示 DS的所有子系统的集合，对F⊆P(DS)且F≠Ø，称B⊆C为DS的代数观点下的F并行约简当且仅当B满足如下2个条件:

1)对任意子表 DT∈F，POSB(DT，D)=POSC(DT，D);

2)对任意S⊂B，至少存在一个子表DT∈F，使得POSS(DT，D)≠POSC(DT，D)．

代数并行约简是保持F中所有子表的正域不变的最小条件属性集合，其结果可能不止一个．因为不需要求出全部子表的所有约简，代数并行约简省略了许多不必要的尝试性计算，因此其算法时间复杂度是多项式级的，而且因为没有求交运算，代数并行约简避免了约简结果为空的情况．

从定义2可以看出，代数并行约简是基于正域不变定义的，在一致决策表中正域涵盖了论域中所有的元素，但是在不一致决策表中论域中部分元素是在正域之外的，而在计算代数并行约简的过程中，正域之外的元素的分类信息是不被考虑的．若决策表的不一致性是由于记录错误或计算误差而产生的，则不考虑正域之外的元素是合理的;但若决策表的不一致性是由于认知不全导致的属性过少而引起的，这么做就有可能造成过约简的问题．

2 基于互信息的并行约简

为了避免并行约简在处理不一致数据时可能产生的过约简问题，本文提出了信息论意义下的并行约简的概念．下面首先介绍其概念和性质．

2．1 概念与性质

定义3 给定一个决策系统DS=(U，C∪D)，P(DS)表示DS的所有子系统的集合，F是P(DS)非空子集合，称B⊆C为DS的信息论意义下的F并行约简当且仅当B满足如下2个条件:

1)对任意子表 DT∈F，I(DT，B;D)=I(DT，C;D);

2)对任意S⊂B，至少存在一个子表DT∈F，使得I(DT，S;D)＜I(DT，B;D)．其中，I(DT，B;D)代表决策表DT中条件属性集B和决策属性D的互信息．

信息论并行约简是保持F中所有子表的互信息不变的最小条件属性集合，其结果可能不止一个．从定义3可以看出，信息论并行约简的概念是基于互信息定义的，因此也可以称为基于互信息的并行约简(Parallel Reducts Based on Mutual Information，简称PRBMI)．当条件属性的集合B发生变化时，正域之外的元素的互信息也会相应变化，这样只要保证约简前后决策表的互信息保持不变，就可以避免因为没有考虑正域之外的元素包含的信息而造成过约简问题．

定义4 给定一个决策系统DS=(U，C∪D)，P(DS)表示DS的所有子系统的集合，F是P(DS)非空子集合．给定PRED为F的信息论并行约简的集合，F的信息论并行约简的核属性PCORE可以定义为

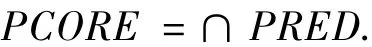
性质1 在一致性决策系统中，代数并行约简和信息论并行约简是等价的;在不一致系统中，代数并行约简是信息论并行约简的子集．

为证明性质1，先要引用文献［7］中的引理1．

引理1［7］给定一个不一致决策系统 DS=(U，C∪D)，B⊆C，若 H(D|B∪{a})=H(D|B)，则POSB∪{a}(D)=POSB(D)，反之则不成立．

引理1说明，一个在代数观点下可以被约简的条件属性(重要性为0)，在信息论意义下不一定是可以被约简的(重要性不一定为0);反之，一个在信息论意义下可以被约简的条件属性(重要性为0)，在代数观点下一定是可以被约简的(重要性一定为0)．利用代数并行约简对一个不一致系统进行约简时，因为没有考虑到正域之外的元素的分类信息，就有可能约简掉一个信息论意义下不能被约简掉的属性，从而造成过约简．

性质1的证明 给定一个不一致决策系统DS=(U，C∪D)，设Q⊂P⊆C，由引理1可知可能存在这种情况:对任意 DT∈F，均有 POSC(DT，D)=POSP(DT，D)=POSQ(DT，D)且 I(DT，C;D)=I(DT，P;D)＞I(DT，Q;D);同时，对任意 Q'⊂Q，P'⊂P，至少存在一个子表 DT∈F，令 POSQ'(DT，D)≠POSQ(DT，D)，I(DT，P';D)≠I(DT，P;D)．由定义2和定义3可知，Q 是 DS代数并行约简，P是 DS信息论并行约简，由此可知在不一致决策系统中，代数并行约简是信息论并行约简的子集．一致性系统中粗糙集代数观点和信息观点的一致性在文献［7］中已经证明，这里不再赘述．

2．2 属性重要度矩阵

文献［5］中代数并行约简算法的属性重要度矩阵是基于正域中元素个数的变化来定义的．下面笔者采用类似的方法定义信息论意义下基于互信息概念的并行约简的属性重要度矩阵(简称基于互信息的属性重要度矩阵)．

定义5 给定一个决策系统DS=(U，C∪D)，P(DS)表示DS的所有子系统的集合，F⊆P(DS)，B⊆C，B关于F的相对D的属性重要度矩阵定义为

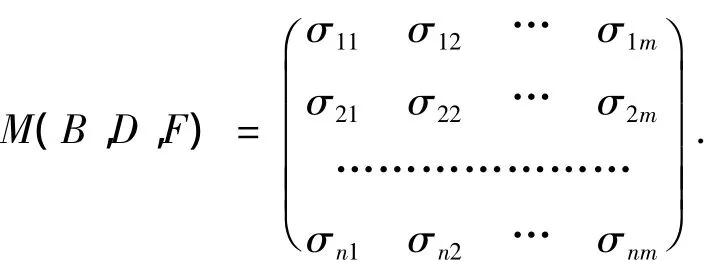
其中:σij= σ(aj，Ui)=Ii(DTi，B;D)-Ii(DTi，B-{aj};D);Ii(DTi，B;D)代表第 i个子系统 DTi中条件属性集B和决策属性D的互信息;aj∈B;(Ui，C∪D)∈F;n代表F中子决策表的个数;m代表DS中条件属性的个数．

矩阵M(B，D，F)中的行反映了B中不同属性在同一子表中相对于决策属性D的分类能力;矩阵中的列反映了同一属性在不同子表中相对于决策D的分类能力．

上面的属性重要度矩阵是一种删除属性式重要度矩阵，下面介绍添加属性式重要度矩阵．

定义6 给定一个决策系统DS=(U，C∪D)，P(DS)表示DS的所有子系统的集合，F⊆P(DS)，B⊆C，B关于F的相对D的属性重要度矩阵定义为

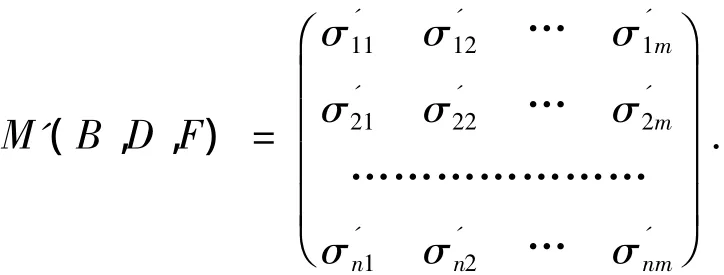
其中:σ'ij= σ'(aj，Ui)=Ii(DTi，B∪{a};D)-Ii(DTi，B;D);aj∈B;(Ui，C∪D)∈F;n 代表 F 中子决策表的个数;m代表DS中条件属性的个数．若aj∈B，则σ'ij的值为 0．

命题1 给定一个决策系统DS=(U，C∪D)，P(DS)表示DS的所有子系统的集合，F⊆P(DS)，M(C，D，F)矩阵中任意大于0的元素对应的属性是其子表在信息论意义下的核属性．

证明 设M(C，D，F)中某一不为 0元素 σij对应的属性为 p，则对子表 i有 Ii(DTi，C;D)-Ii(DTi，C-{p};D)＞0．对任意 B⊆C，若 p∉B，则必有 Ii(DTi，C;D)＞Ii(DTi，B;D)，由定义3 可知 B 一定不是子表i的约简．由此可知，对子表i的任意约简都包含属性p，即属性p为子表i的核属性．综上所述，M(C，D，F)矩阵中任意大于0的元素对应的属性是其子表在信息论意义下的核属性．命题1证毕．

命题2 给定一个决策系统DS=(U，C∪D)，P(DS)表示DS的所有子系统的集合，F⊆P(DS)．若矩阵M(B，D，F)中某一列元素全大于0，则该列对应的属性为信息论意义下F并行约简的核属性．

命题2可由命题1和定义4简单推出，不再赘述．

2．3 基于互信息的并行约简算法

接下来介绍基于互信息的并行约简算法，该算法的主要思想是先从矩阵M(C，D，F)中找到信息论并行约简的核，然后依次把矩阵M'(B，D，F)中最好的属性添加到约简中并进行迭代，直到M'(B，D，F)中所有的元素均为0为止．算法的具体步骤如下:

输入:F⊆P(DS)．

输出:F的一个并行约简．

第1步:建立属性重要度矩阵M(C，D，F)．

第2 步:B=∪mj=1{aj:∃σkj(σkj∈M(C，D，F)∧σkj≠0)}，B 是 F 中所有子表的核属性．

第3 步:计算 M'(C，D，F)．

第4步:重复进行如下步骤，直到M'(C，D，F)中全部元素都为0:

第5步 输出约简B．

接下来评估一下这个算法的时间复杂度．可以看出，基于互信息的并行约简算法(以下简称PRBMI算法)和文献［5］中的Parallel Reducts Based on Attribute Significance算法(简称PRBS算法)的框架和流程基本相同，只是对属性重要性的定义方式不同．在PRBS算法中属性重要度是利用正域个数的变化来定义的，只需要进行一次减法运算和除法运算即可;而在PRBMI算法中属性重要度是利用互信息的变化来定义的，需要进行若干次(具体次数和划分出来的等价类的个数有关)除法运算和对数运算．因此从理论上来讲，PRBMI算法的时间复杂度总是比PRBS算法高．在实际实验中，算法的大部分时间开销都花在等价类的划分上，计算属性重要度的时间开销其实非常小，可以略去不估，因此能够认为PRBMI和PRBS的时间复杂度是相同的，都是O(nm3|U'||log2|U'||)．其中:n代表决策子表的个数;m代表条件属性的个数;|U'|代表最大决策子表中记录的个数．

3 实验

本文所有的实验数据均来自UCI数据库，实验时从原决策表中随机抽取了10个子表，第1个子表包含原决策表40%的数据，第2个子表包含原决策表46．7%的数据，依次递增，最后一个子表包含原决策表100%的数据．实验机器的硬件配置为:Computer Model:Lenovo Ideapad Y430;CPU:Intel Pentium(R)Dual-Core T4200@2．0 GHz;Memory:2 048 MB RAM;Hard disk:250 G;OS:Windows 7 ultimate SP1．实验的最终结果如表1所示．

表1 代数并行约简与信息论并行约简的比较

可以看出，PRBS算法和PRBMI算法的时间开销基本相同，甚至对于某些数据，PRBMI算法的时间开销比PRBS还要小，这是因为PRBMI算法在划分条件和决策都相同的等价类时可以利用已经划分出的条件等价类中的信息，而PRBS算法在划分决策等价类时不能利用这些信息．

4 结语

本文对并行约简理论进行了拓展，将并行约简理论由代数观点下拓展到了信息论意义下，提出了信息论意义下的并行约简——基于互信息的并行约简;探讨了代数论意义下的并行约简和信息论意义下的并行约简的一致性和差异性;利用互信息的概念定义了信息论意义下的属性重要度矩阵，并基于该矩阵构造了基于互信息的并行约简算法;最终通过实验验证了信息论意义下的并行约简和代数意义下的并行约简具有相同的时间复杂度这一论断．

［1］Bazan J G．A comparison of dynamic non-dynamic rough set methods for extracting laws from decision tables［C］//Polkowski L，Skowron A．Rough sets in knowledge discovery 1:Methodology and applications．Heidelberg:Physica-Verlag，1998:321-365．

［2］Bazan J G，Nguyen H S，Nguyen S H，et al．Rough set algorithms in classification problem［C］//Polkowski L，Tsumoto S，Lin T Y．Rough set methods and applications．Heidelberg:Physica-Verlag，2000:49-88．

［3］Deng Dayong．Parallel reducts and its properties［C］//Proceedings of 2009 IEEE International Conference on Granular Computing．Lushan:IEEE，2009:121-125．

［4］Deng Dayong，Yan Dianxun，Chen Lin．(F，ε)-parallel reducts in a series of decision subsystems［C］//The Third International Joint Conference on Computational Sciences and Optimization(CSO2010)．Huangshan:IEEE，2010:372-376．

［5］Deng Dayong，Yan Dianxun，Wang Jiyi．Parallel reducts based on attribute significance［C］//The 5th International Conference of Rough Set and Knowledge Technology(RSKT 2010)．Beijing:Springer，2010:336-343．

［6］Deng Dayong，Yan Dianxun，Wang Jiyi，et al．Parallel reducts and decision system decomposition［C］//Proceedings of the Fourth International Conference on Computational Sciences and Optimization(CSO 2011)．Kunming:IEEE，2011:799-803．

［7］王国胤．Rough集理论代数与信息论观点的关系研究［J］．世界科技研究与发展，2002，24(5):20-26．