基于决策等价性的决策表属性集分解研究*

张 政 胡 沛

(南阳理工学院软件学院 南阳 473000)



基于决策等价性的决策表属性集分解研究*

张 政 胡 沛

(南阳理工学院软件学院 南阳 473000)

决策表属性集分解是处理决策大型决策表数据复杂性,提高数据分析的一种有效手段,已得到深入研究。但在属性集分解过程中,有可能出现决策规则的泛化,从而导致从原决策表与从子决策表得到的规则不一致性。论文深入研究了决策表属性集分解的等价性问题,从保持决策表等价性和提高子表分类质量的角度,提出了基于决策等价的决策表属性集分解方法,并与现有的属性集分解方法做了比较。

决策表; 属性集; 分解; 等价性

Class Number TP18

1 引言

传统的数据挖掘和知识归纳方法在决策表分析和处理中得到了较好的应用,但是随着计算机和数据采集技术的进步,许多大型决策表包含了大量的属性和对象,如何从这些堆积如山的数据中挖掘有用的信息,已成为当今数据挖掘领域的热点[1]。

决策表分解是解决大型决策表数据海量性和复杂性问题的一种有效手段。其思想是将一个大型决策表分解为若干规模较小且易于处理的子表,在子表中进行规则获取,可以减少每次处理的数据量,避免直接在复杂系统中建模的困难和缺陷,提高数据分析的效率和质量[2]。

本文提出了基于决策等价性的决策表属性集分解方法。首先根据决策表属性集分解的等价性,提出了决策等价性判定标准,然后从决策等价和提高决策分类质量的标准出发,提出了一种新的条件属性选择量度,按照属性选择量度指导子决策表的属性选取,将决策表分解为几个决策等价的子决策表。

2 粗糙集理论基本概念

粗糙集理论是波兰数学家Z.Pawlak于1982年提出的一种处理含糊和不确定性问题的新型数学工具,已经在机器学习、数据挖掘等领域中得到广泛应用,决策表信息系统是粗糙集理论的主要研究对象[3]。

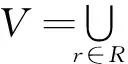
定义2 在决策表信息系统S=〈U,R,V,f〉中,对于B⊆R,则B在U上的不可分辨关系定义为

(1)

显然IND(B)是一个等价关系,它的所有等价类的集合记为U|IND(B),简记为U|B。

定义3 给定决策表信息系统S=〈U,R,V,f〉,对于每个子集X⊆U和不可分辨关系B,X的下近似集和上近似集可以分别定义为

B-(X)=∪{Yi|(Yi∈U|IND(B)∧Yi⊆X)}

(2)

B-(X)=∪{Yi|(Yi∈U|IND(B)∧Yi∩X≠φ)}

(3)

定义4 设U为一个论域,P、Q为U上的两个等价关系簇,Q的P正域POSP(Q)定义为

(4)

相对正域POSP(Q)是论域U的所有那些使用分类U|P所表达的知识中能够正确地分类到U|Q的等价类之中的对象的集合。

(5)

定义6F是属性集D导出的分类,C是条件属性集合,D={d}是决策属性集合,且A⊂C则对于任意属性a∈C-A的重要性SGA(a,A,D)为

SGA(a,A,D)=rA∪{a}(F)-rA(F)

(6)

3 等价的决策表属性集分解

决策表属性集分解是从给定原始属性集中按照一定的标准选取属性结成一组,然后按照一定的算法来识别定义在属性组上的中间概念层次,从而到达降维、增强模型可理解性的目的。这一方法要求在保持模型的分类能力的前提下,简化计算并增强模型的可理解性。

决策表属性集分解减少了每次处理的数据量,使得适合普通决策表的算法也能适用于复杂的大型决策表,各子表之间可以进行并行计算,减小时间复杂度,提高数据分析的效率。目前决策表属性集分解方法主要有：基于函数的分解方法[4],基于属性核的分解方法[5]和基于属性聚类的分解方法[6]；这些属性集分解方法虽得到了较好的应用,但由于没考虑到分解前后决策等价性的问题,致使得到的决策存在规则泛化的可能。本文以分解前后决策等价为标准,从提高子决策表条件属性分类能力出发提出了新的决策表分解属性集方法,使其能保持分解前后决策等价性。对于含有多个决策属性的决策属性集D,可以将其转换为单一的决策属性[7],本文中只考虑决策属性集只包含一个决策属性d的情况,即D={d},S=〈U,C∪D,V,f〉。

3.1 决策表属性集分解的等价性

决策表分解的决策等价性是指通过原决策表归纳所得到的决策结果与分解后综合各子表局部规则得到的决策结果相同[8～9]。属性集分解过程中,由于子决策表属性个数减少,仅由部分条件属性推导的规则可能出现泛化,增大了分类决策的不确定性。

3.2 决策表分解条件属性的选择

为了提高子决策表的决策分类质量,子表条件属性的选取从属性重要性和近似分类质量考虑,子表条件属性的选取需满足以下条件：

1) 选入子表的第一个条件属性b需要对论域有最大的正域分类能力,即单条件属性集{b}需有最大的近似分类质量rB(F)；

2) 选入子表的其它条件属性需对决策分类起很好的辅助作用,即相对于当前子表中的条件属性集A,要有最大的属性重要性SGA(a,A,D)。

3.3 属性集分解等价性判定

首先考虑将原决策表S分解为两个子决策表S1和S2的情况,它们对应的条件属性子集分别为C1和C2。如果对于∀u∈U,δC(u)=δC1(u)∩δC2(u),则该分解是一次等价的属性集分解；如果有δC(u)⊂δC1(u)∩δC2(u),则该分解不是等价的属性集分解,需要在表S2中增加相应的分类信息,具体方法为：

找出决策规则信息丢失对象R,即论域中所有δC(u)⊂δC1(u)∩δC2(u)的对象,在表S2增加相应分类条件属性集C′,且C′与R的关联度为1；为了保证C′个数尽可能少,应从单属性考虑,如果单属性集与R的关联度不为1,则考虑使用属性组合。S分解为多个子表的等价性判定与分解为2个子表的方法类似。

3.4 算法描述

输入：大型决策表S=〈U,C∪D,V,f〉；其中U为论域,C,D分别为条件属性集和决策属性集。

输出：一系列符合要求的子表。

算法1.DDBDE

Step1. 设置每个子表所允许的最大条件属性集个数为n′(n′由用户实际需要设置或由专家结合问题的先验知识确定)。

Step2. 设决策属性D的等价类：F=U|D={D1,D2,…,Dm},用式(5)计算C中各单属性集的近似分类质量,取满足：MAX(rB(F))的属性x；j=0,Rj=Φ,k=0。

Step3. 将x并入集Rj中,k++。若C=Φ,跳到Step7执行。若C≠Φ,判断是否满足k≤n,如果满足的话,执行Step4；如果不满足,执行Step2。

Step4. 用式(6)求出C中各属性的属性重要性,取满足MAX(SGA(a,Rj,D))的条件属性y,将y加入Rj,C=C-Rj。

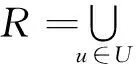
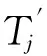
Step8. 输出各子表Si(0≤i≤j)。

4 改进的决策表属性集分解

为了保证属性集分解的等价性,算法DDBDE需要在每次分解完成后要判断从子表得到的决策属性交集与原决策表的决策值是否相等,需要大量的运算,不利于提高算法的效率。

rB(Xi)=|B_(Xi)|/|U|

4.1 子决策表条件属性的选择

1) 选入子表的第一个条件属性b需要对论域有最大的正域分类能力,即单条件属性集{b}需有最大的近似分类质量rB(F)；

2) 选入子表的其它条件属性需对决策分类起很好的辅助作用,即相对于当前子表中的条件属性集A,要有最大的属性重要性SGA(a,A,D)。

4.2 属性集分解等价性判定

首先考虑将原决策表S分解为两个子决策表S1和S2的情况,它们对应的条件属性子集分别为C1和C2。如果POSC1(D)∪POSC2(D)=U,则该分解是一次等价的属性集分解；如果POSC1(D)∪POSC2(D)⊂U,表明本次分解可能不是等价的,导致决策正域分类信息丢失,对子表S2应增加相关的决策正域分类信息。具体方法如下：

找出决策正域分类信息丢失对象R=U-(POSC1(D)∪POSC2(D)),在表S2增加相应决策正域分类条件属性集C′,使rC′(R)=1,且C′⊆C1；为了保证C′个数尽可能少,应从单属性考虑,如果单属性集不能对R正确分类,则考虑使用属性组合。S分解为多个子表的等价性判定与分解为2个子表的方法类似。

4.3 算法描述

算法2.ADDBDE

Step1. 设置每个子表所允许的最大条件属性集个数为n′(n′由用户实际需要设置或由专家结合问题的先验知识确定)。

Step2. 设决策属性D的等价类：F=U|D={D1,D2,…,Dm},用式(5)计算C中各单属性集的近似分类质量,取满足：MAX(rB(F))的属性x；j=0,Rj=Φ,k=0。

Step3. 将x并入集Rj中,k++。若C=Φ,跳到Step7执行。若C≠Φ,判断是否满足k≤n,如果满足的话,执行Step4；如果不满足,执行Step2。

Step4. 用式(6)求出C中各属性的属性重要性,取满足MAX(SGA(a,Rj,D))的条件属性y,将y加入Rj,C=C-Rj。

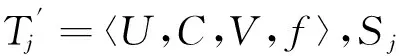
Step6.R=U-(POSRj(D)∪POSC-Rj(D)),如果R=Φ,表明此次分解为等价的属性集分解,如果R≠Φ,表明此次分解有决策正域分类信息丢失,需要在C中增加相应分类信息C′,且rC′(R)=1,C′⊆Rj,|C′|的值应最小,将C′并入C中。

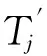
Step8. 输出各子表Si(0≤i≤j)。

4.4 属性集分解方法的比较

满足算法ADDBDE的决策等价判定必满足算法DDBDE的等价判定,故ADDBDE可以看作是DDBDE的特例,满足ADDBDE的等价分解必满足DDBDE,因此ADDBDE中的冗余条件属性个数大于或等于DDBDE中的冗余条件属性数；但ADDBDE只需计算各子表的正域分类情况,无需推导相应的决策规则,比DDBDE具有较小的时间复杂度和空间复杂度。

SGA(a,A,Xi)=rA∪{a}(Xi)-rA(Xi)。

定理2 决策表S=〈U,C,D,V,f〉,如果POSC′(D)∪POSC-C′(D)=U,则rC′(F)≥SGA(C′,C,D)。

证明 因为|POSC′(D)∪POSC-C′(D)|=|POSC′(D)|+|POSC-C′(D)|-|POSC′(D)|∩|POSC-C′(D)|=|U|。

即rC′(F)-(|POSC′(D)|∩|POSC-C′(D)|)/|U|=SGA(C′,C,D)

故rC′(F)≥SGA(C′,C,D)。

证毕。

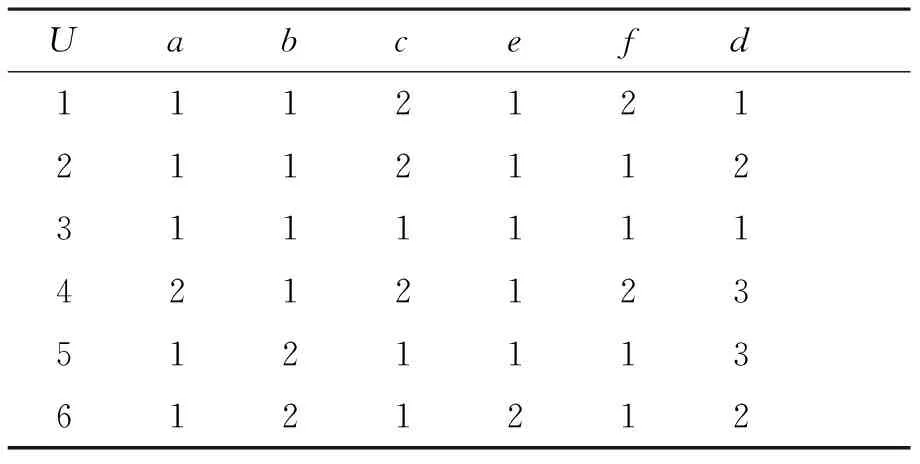
推论1 如果rC′(F)

表1从分类质量、决策等价性、时间复杂度等方面对上述几种决策表属性集分解方法进行比较。

表1 决策表属性集分解方法的比较

5 基于决策分类的决策表分解实例

如表1所示的决策表,C={a,b,c,e,f,g}是条件属性集合,D={d}是决策属性集合。下面利用本文所提到的基于决策等价的决策表属性集分解方法对决策表2进行属性集分解。

表2 决策表1

用算法DDBDE可以将其分解成表3和表4。

表3 子决策表1

表4 子决策表2

用算法ADDBDE可以将其分解成表5和表6。

表5 子决策表3

表6 子决策表4

6 结语

从决策表中快速有效地提取规则是决策表分解的主要目的。分解前后决策分类的等价性是影响决策表分解质量的关键因素,在分解过程中要力求保证决策等价和信息无损,避免决策表分解对分类结果带来的不确定性。本文提出了两种基于决策等价的属性集分解方法,分解的每次过程都保证了分解的等价性,使决策表分解前后从原表与从子表得到的规则一致；并从分类质量、决策等价性和时间复杂度等方面与传统的属性集分解方法做了比较。

[1] Z.Pawlak. Theorize with Data using Rough Sets[C]. Proceedings of the 26th Annual International Computer Software and Applications Conference.IEEE， 2002.

[2] 王加阳, 刘柳明, 罗安. 大型决策表分解方法研究[J].计算机科学，2007，34(8)：211-214. WANG Jiayang, LIU Liuming, LUO An. Research on Decomposition of Large Decision Table[J]. Computer Science，2007，34(8)：211-214.

[3] Z.Pawlad.Rough Sets[J].International Journal of Computer and Information Sciences，1982，11：341-356

[4] B. Zupan, M. Bohanec, I. Bratko, et al. A Dataset Decomposition Approach to Data Mining and Machine Discovery[C]//D. Heckerman eds. Proc. of the Third International Conference on Knowledge Discovery and Data Mining. Irvine, CA: AAAI Press,1997:299-303

[5] 樊群，赵卫东，达庆利.一种基于粗集的实例分解归纳学习方法[J].管理工程学报，2001，15(2)：79-81. FAN Qun，ZHAO Weidong，DA Qingli. A Decision Table Decomposition Induction Learning Method Based on Rough Set[J]. Journal of Industrial Engineering and Engineering Management，2001,15(2)：79-81.

[6] 杨善林，刘业政，李亚飞.基于Rough Sets理论的证据获取与合成方法[J].管理科学学报，2005，8(5)：69-75. YANG Shanlin，LIU Yezheng，LI Yafei. Research on Rough Sets-based Evidence Acquirement and Combination of DST[J].Journal of Management Sciences，2005,8(5)：69-75.

[7] 刘业政.基于粗糙集数据分析的智能决策支持系统研究[D].合肥：合肥工业大学，2003:23-24. LIU Yezheng. Research on Rough Set Data Analysis Based Intelligent Decision Support Systems[D]. Hefei：HeFei University of Technology，2003:23-24.

[8] Kusiak. A. Decomposition in Data Mining: A Medical Case Study[C]. In: B.V.Dasarathy, eds. Proceedings of the SPIE Conference on Data Mining and Knowledge Discovery: Theory, Tools, and TechnologyⅢ. Orlando,2001:267-27.

[9] 刘柳明，王加阳，罗安.决策表属性集分解的等价性研究[J].计算机应用研究，2007，24(8)：67-69. LIU Liuming，WANG Jiayang，LUO An. Research on Equivalence of Attribute Set Decomposition to Decision Table[J]. Application Research of Computers，2007,24(8)：67-69.

[10] Hadjimichael M.,Wong S.K.M.,Ziarko W. Rough Sets:Probabilistic versus Deterministic[J]. International Journal of Man-Machine Studies,1988,29(29):81-95.

[11] Ziarko W. Analysis of uncertain information in the framework of variable precision rough sets[J]. Foundations of Computing and Decision Science 1993,18(3/4):381-396.

Attribute Set Decomposition of Decision Table Based on Decision Making Equivalence

ZHANG Zheng HU Pei

(College of Software, Nanyang Institute of Technology, Nanyang 473000)

Attribute set decomposition of decision table as a useful method deals with data complexities of the large decision tables and improves data analysis. It had in-depth studied by many scholars. But it may appears decision rules generalization during the attribute set decomposition, so it may led differences of the rules from the original decision table and the child decision tables. The paper went deep into the equivalence of attribute set decomposition, and proposed novel attribute set decomposition approaches from keeping the equivalence of decision table and improving the classification rate in the child decision tables and compared the methods with existing methods of attribute set decomposition.

decision table, attribute set, decomposition, equivalence

2016年5月16日,

2016年6月30日

张政,男,硕士，讲师，研究方向：数据挖掘、粗糙集理论及应用、云计算与大数据。胡沛,男, 硕士,讲师，研究方向：嵌入式、数据挖掘、粗糙集理论及应用。

TP18

10.3969/j.issn.1672-9722.2016.11.026