二维Josephson结阵列超导的涡旋Nernst效应＊

祁 飞， 吕建平， 刘 焕， 陈庆虎，2

(1．浙江师范大学数理与信息工程学院，浙江金华 321004;2．浙江大学物理系，浙江杭州 310027;3．中国矿业大学物理系，江苏徐州 221116)

Nernst效应是一种有磁场情况下的热电效应．在金属或者超导体的一个方向加入温度梯度，在横向会产生一个电场响应．对于正常态金属材料而言，Nernst信号很小，但对于第二类超导体，在超导转变温度Tc以下有显著的Nernst信号．令人惊讶的是:在Tc以上，本预计较小的Nernst信号却大得反常，这已引起了广泛的关注［1-4］．对于这种反常，一种解释为即使在超导转变温度以上，超导凝聚也已出现，只是没有相干凝聚，从而并未产生超导电性．超导凝聚(或称预配对)是反常的Nernst效应的起源．

通常来说有2种因素可导致Nernst效应:一种来源于准粒子;另一种来源于涡旋．Ong研究小组［3］的实验表明，对于单层铜氧面的Bi-2201超导体，涡旋的贡献是主要的，而对YBCO超导体，准粒子和涡旋都对Nernst效应有贡献．目前的实验研究对区分准粒子和涡旋对Nernst效应的贡献仍十分困难．

本文模拟二维Josephson结阵列的电压对温度梯度的响应，模拟高温超体的涡旋Nernst信号．其结果适用于涡旋起主要贡献的高温超导体，如Bi-2201超导体．

1 理论模型与模拟方法

在正方格子上的二维Josephson结阵列可用以下二维XY模型的哈密顿量描述:

式(2)中:Γ是决定驰豫的时间标度;Γi(t)在i点的热涨落引起的噪声电流满足高斯分布

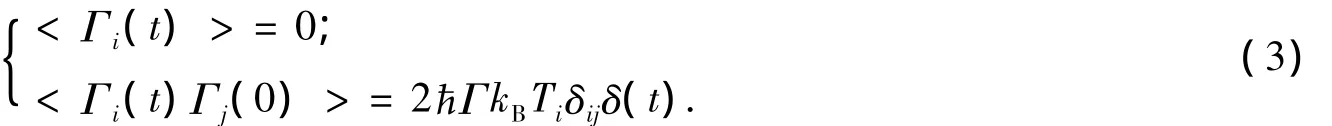
式(3)中，Ti为第i个格点的温度．

在笔者的模拟中，时间和温度的单位为ħ/(ΓJ0)和J0/kB．为方便起见，按惯例，单位采用约化形式，即令J0=ħ=kB=1．

磁场加在Z方向，温度梯度加在X方向，因此，在该方向取开边界条件．在X方向各格点的温度以线性关系增加，则第i个格点的温度为

式(4)中:T0为整个系统的平均温度;δt是控制温度梯度大小的参量．在模拟中，笔者取δt=0．1;i表示第i个格点．

在Y方向采用涨落扭转边界条件，保持相位的周期性，这样可以在此方向应用快速Fourier变换，如此可极大地提高计算效率．涡旋在热驱动下便由高温的一端向低温的一端运动．利用涨落扭转边界条件［5-6］直接测量Y方向上的电压Vy．Nernst信号可由电压计算得到

结合温度梯度的具体加法，Nernst信号可以表示成

利用式(6)可直接计算Nernst信号的强度．

2 模拟结果与讨论

为了确认模拟方法的可靠性，笔者首先模拟了该系统在电流驱动下不同磁通密度下的电阻值．在Josephson结阵列模型中，对于不同驱动电流、温度，系统的电压曲线随磁通密度的增加呈现出明显的先升后降的过程，图1所示为该模型的V/I-f曲线．图1中:I表示外加驱动电流;T表示系统温度．该曲线在一些特定的磁通密度f下，如f=1/8，1/6，1/5，1/3，2/5，1/2等位置时出现系统电阻的极小值，且在这些特殊磁通密度下，涡旋会呈现出一定的规则排列．图2所示为笔者模拟的系统在这些特殊磁通密度f下的涡旋在实空间中的分布．这些结论与文献［7-8］的实验结果基本一致，侧面反映了本小组在研究二维Josephson结阵列的物理性质时所用的模拟方法是可靠的．

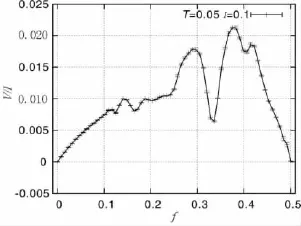
图1 V/I-f曲线

图2 超导涡旋在实空间的分布(白色格点表示涡旋所在位置)

将上述的电流驱动换成热驱动，便可以计算Nernst信号．表1给出了在T0=0．6稳定时的几种温度梯度与Nernst信号的关系．显然，改变式(6)中参量δt对Nernst信号影响不大，这一点说明了Nernst效应是系统的本征性质，而与温度梯度的具体大小无关．

表1 不同温度梯度下的 Nernst信号(T=0．6，f=0．125，L=64)

现在计算不同温度下二维 Josephson结系统的Nernst信号与外加磁场的关系．无外场的二维Josephson结系统经历Kosterlitz-Thouless相变，相变温度为Tc=0．890 4J0，这个温度也是超导相变温度．因此，笔者特定选取温度T的范围为0．2～1．2，既包含了超导相变温度以下又包含了相变温度以上的情形．数值模拟获得的Nernst信号如图3所示．为了研究尺寸带来的效应，笔者分别研究了尺寸L为32和64两种大尺寸系统．其结果定性上没有改变，说明笔者选取的系统尺寸所获得的结果是可靠的．

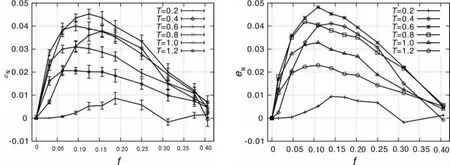
图3 不同温度下Nernst信号曲线图(左图系统尺寸大小L=32;右图系统尺寸大小L=64)

接下来分析其物理结果．首先，在超导转变温度(0．890 4)以上，如T=1．0和T=1．2两种情况，系统的Nernst信号还是非常显著的，这与高度各向异性的高温超导在超导转变温度以上出现反常现象的Nernst信号完全一致［2］．其次，系统的Nernst信号随外加磁场和温度的增大都呈现出非单调行为，与单层铜氧面的Bi-2201超导体的Nernst信号的实验结果完全一致．曲线的外形也与实验结果一致，显示了倾斜山丘的形貌(tilt-hill profile)．另外，“山脊”的位置大约在f=0．1处，也与实验结果B=0．1Bc2一致．Bc2为上临界磁场，可以大致定义为系统的磁场足够大以致涡旋芯子占据了整个超导样品．这里，f的定义也正是这种填充因子(filling factor)的意思，f最大可以为1．

可以定性给出在恒定温度下系统的Nernst信号随外加磁场非单调行为的物理解释．在低磁场下，涡旋之间的相互作用可以忽略，因为涡旋比较稀薄，所以当磁场升高时，自由涡旋的Nernst信号可以线性叠加．在高磁场时，高密度的涡旋之间强相互作用阻止涡旋的热运动，导致非常小的Nernst信号．这两种机制存在竞争，在居间磁场下必然会产生一个极大值．在高于超导转变温度下，由于出现大量的涡旋-反涡旋激发，这也增加了涡旋的密度，导致Nernst信号下降，这就说明了随温度的升高Nernst信号下降的原因．

近年来，Andersson等［9］也给出类似模型的Nernst信号模拟结果，他们发现Nernst信号随温度升高单调地下降，与笔者的结果不一致，当然也不能描述实验结果．该研究小组采用的小尺寸(L=16)并不是主要原因，因为笔者也模拟了L=16的系统，并没有获得与其相似的结果，而是得到与L=32系统定性一致的结果．笔者认为，他们的数值模拟方法在电压的方向上也采用了开边界条件，因此可能带来强烈的边界效应．笔者在电压的方向采用了涨落扭转边界条件，实际上消除了边界的阻碍．小尺寸可能加剧了这一边界效应．

3 结论

利用XY模型模拟了二维Josephson结阵列在热驱动下的Nernst信号，可以直接计算Josephson结阵列中的涡旋Nernst信号．发现涡旋Nernst信号随磁场变化非单调变化行为，与Princeton大学Ong教授研究组在最佳掺杂和欠掺杂的Bi-2201单晶的实验结果定性符合．涡旋Nernst信号随着平均温度变化亦非单调变化，而是随着磁平均温度的增大皆是先增加、后衰减．归根结底，外加磁通密度及平均温度改变了系统中涡旋的数目、性质及运动状态．二维Josephson结是一个可以控制和调控的实际系统，该系统的研究结果可以提供第二类超导电性的涡旋Nernst信号的产生机制，因而具有重要的意义．

［1］Podolsky D，Raghu S，Vishwanath A．Nernst effect and diamagnetism in phase fluctuating superconductors［J］．Phys Rev Lett，2007，99:117004．

［2］Xu Zhuan，Ong N P，Wang Y，et al．Vortex-like excitations and the onset of superconducting phase fluctuation in underdoped La2-xSrxCuO4［J］．Nature，2000，406:486-488．

［3］Wang Yayu，Li Lu，Ong N P．Nernst effect in high-Tcsuperconductors［J］．Phys Rev B，2006，73:024510．

［4］Li Lu，Wang Yayu，Naughton M J，et al．Magnetization，Nernst effect and vorticity in the cuprates［J］．Journal of Manetism and Manetic Materials，2007，310:460-466．

［5］Chen Qinghu，Tang Leihan，Tong Peiqing．Anomalous finite-size effect in superconducting josephson junction arrays［J］．Phys Rev Lett，2001，87:067001．

［6］Kim B J，Minnhagen P，Olsson P．Vortex dynamics for two-dimensional XY models［J］．Phys Rev B，1999，59:11506-11522．

［7］Baek I C，Yun Y J，Lee J I，et al．Superconducting transition of a two-dimensional Josephson junction array in weak magnetic fields［J］．Phys Rev B，2005，72:144507．

［8］Teitel S，Jayaprakash C．Josephson-junction arrays in transverse magnetic fields［J］．Phys Rev Lett，1983，51:1999-2002．

［9］Andersson A，Lidmar J．Anomalous Nernst effect an heat transport by vortex vacancies in granular superconductors［J］．Phys Rev B，2010，81:060508．