冷贮备可修复系统解的指数渐近稳定性＊

胡晓晓， 谢观湧

(温州医学院信息与工程学院，浙江温州 325035)

冷贮备系统多被应用在工业上，已有许多学者对此进行研究［1］．本文通过证明系统算子可以生成正压缩C0半群，得到T(t)是拟紧算子，并进一步指出系统算子的豫解集是右半平面和虚轴上除0点以外的所有点．由此推出:该系统的时间依赖解，当时间趋向于无穷时，以指数形式收敛于系统的稳态解．

由文献［1］得到的系统可以由以下方程组描述:

式(1)中:(x，t)∈［0，∞］×［0，∞);p0(t)表示一个部件在工作，另一个部件在t时刻冷贮备的概率;p1(x，t)dx表示在(x，x+dx)内一个部件工作，另一个部件在维修的概率;p2(x，t)dx表示在(x，x+dx)内一个部件在维修，另一个部件在等待维修的概率;λ表示部件的故障率;μ(x)是风险函数，且满足

取状态空间

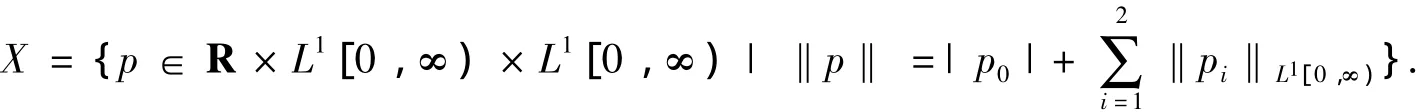
显然，X是Banach空间．记

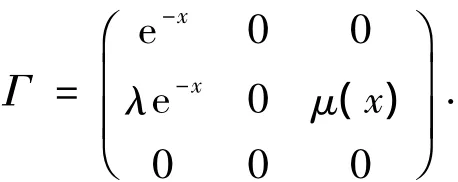
同时引进算子A，B，E及其相应的定义域．

这样，方程组(1)可改写为Banach空间X中的抽象Cauchy问题

定理1 A+B+E生成正压缩C0半群T(t)．

因为E是紧算子，因此可由文献［2］中的命题2．9推出以下结论:

定理2 A+B生成正压缩C0半群S(t)．

本文首先证明S(t)是拟紧算子;其次，由E的紧性得到T(t)是紧算子;然后，证明0是算子A+B+E和其共轭算子(A+B+E)*几何重数和代数重数为1的特征值;最后，利用文献［2］中的定理5得到本文结论．

命题1 若p(x，t)=(S(t)φ)(x)是以下方程的解:

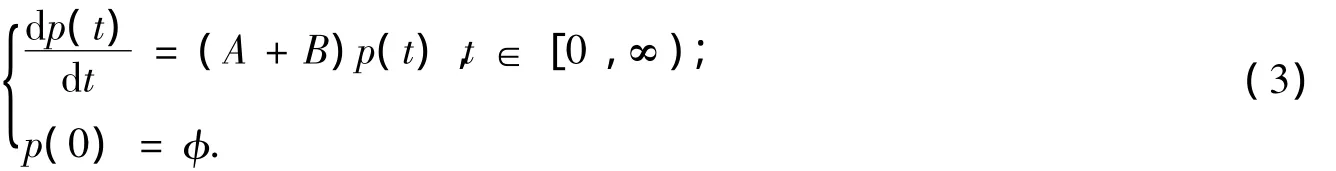
则

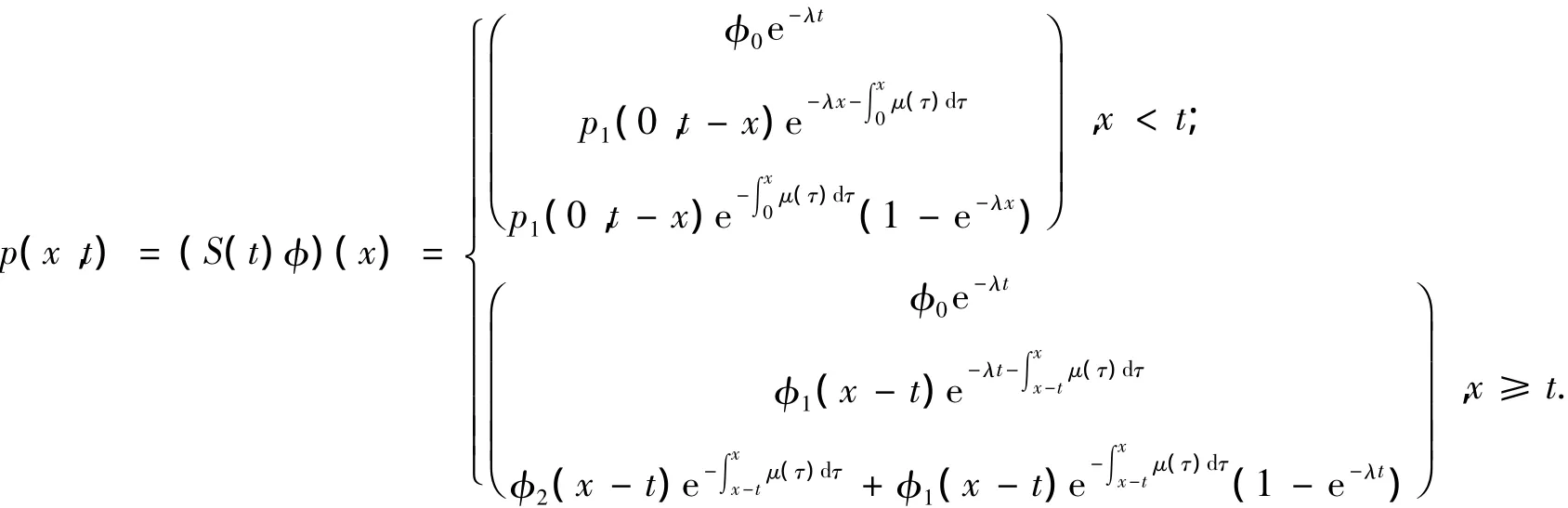
证明 因为p(x)是方程(3)的解，所以

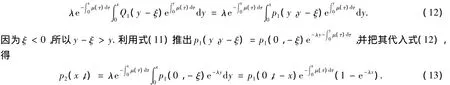
由式(4)和式(9)得

若 ξ≥0(即 x≥t)，则对式(10)由 0 到 t积分，且由 Q1(0)=p1(ξ，0)=φ1(x－ t)，Q2(0)=p2(ξ，0)=φ2(x－t)知，方程(10)的解类似于式(11)～式(13)，于是

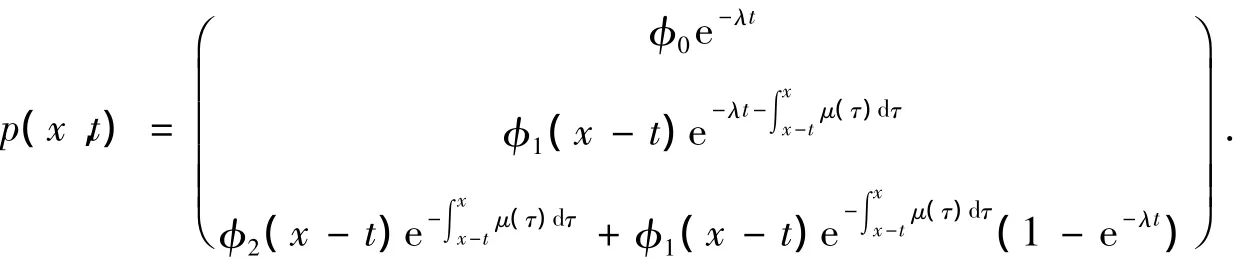
命题1证毕．

现在定义以下2个算子(p∈X):

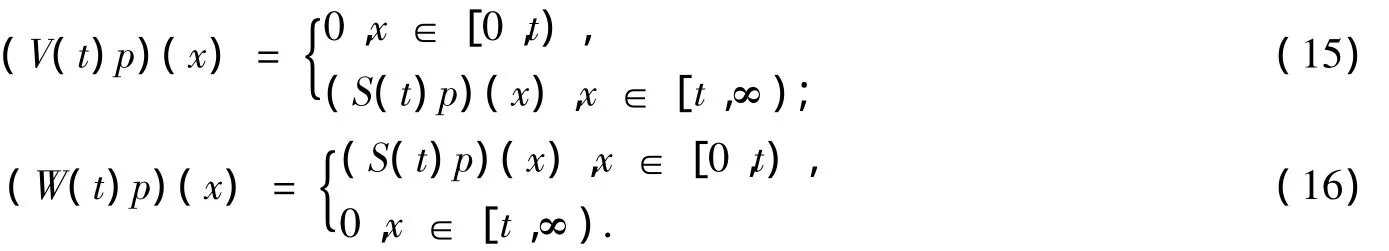
则S(t)p=V(t)p+W(t)p．

由引理1和文献［4］可以得到以下结论:

引理2 X中的有界闭子集M是紧的，当且仅当以下2个条件成立:

证明 与文献［5］中的证明类似，故略．

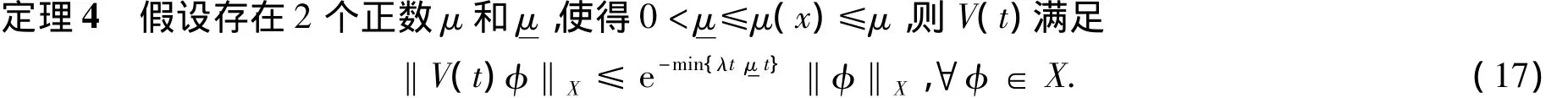
证明

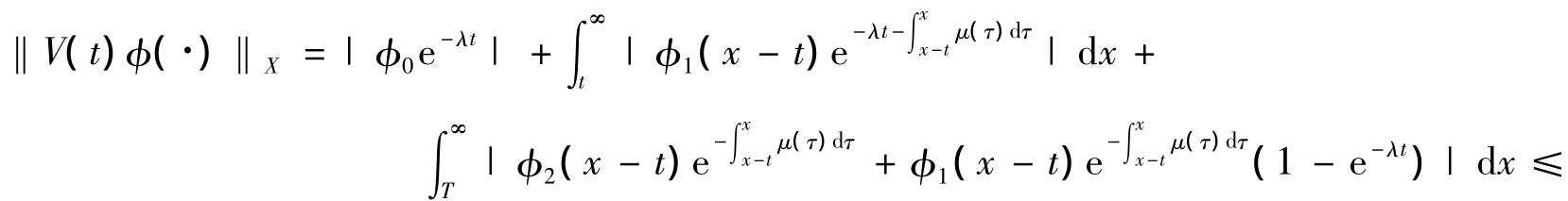
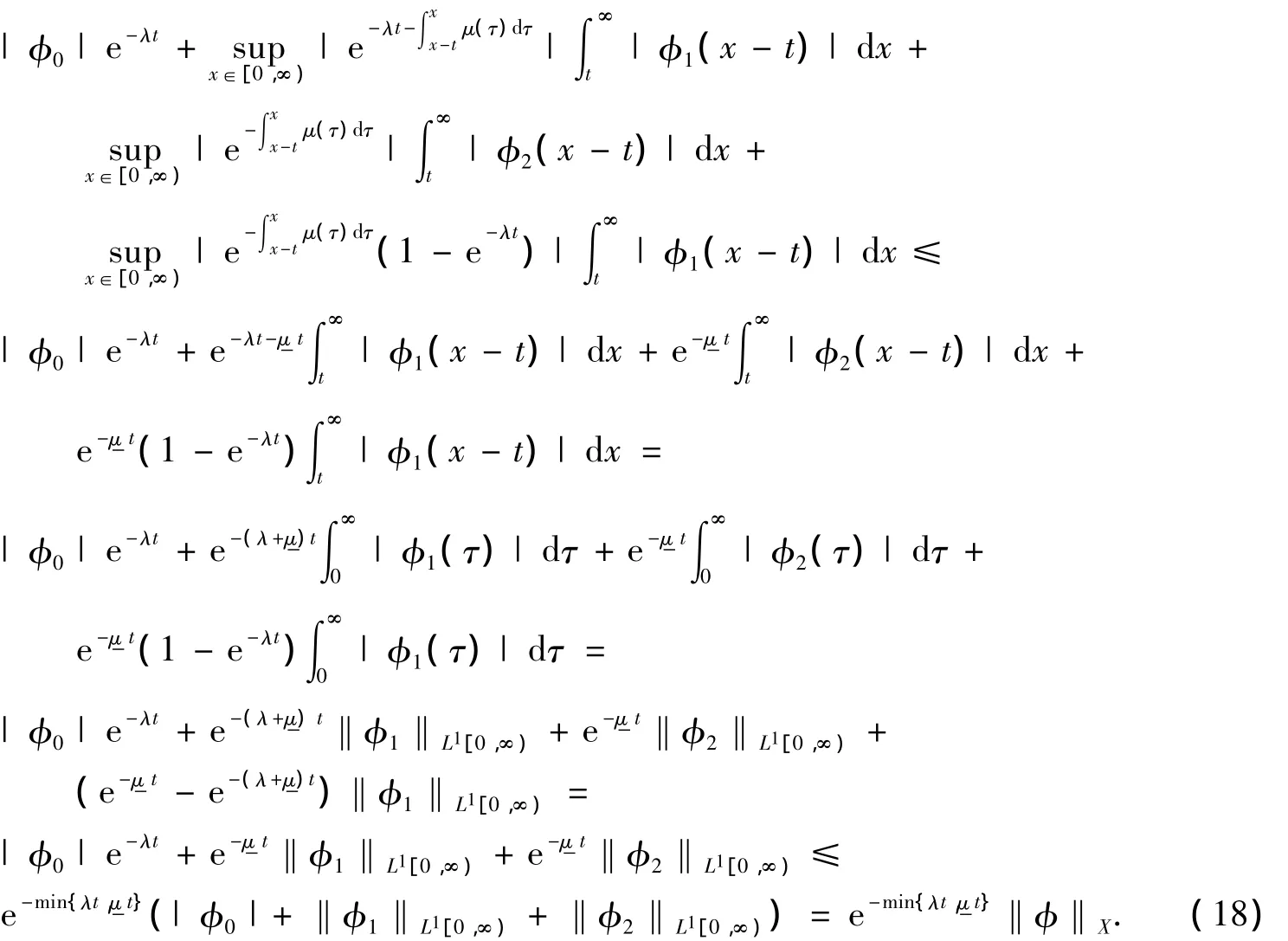
定理4证毕．

由定理3和定理4可以推出

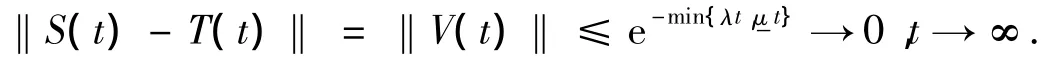
结合文献［2］中的定义2．7可以得到以下结论:

定理5 S(t)是X的拟紧算子．

因为E是X上的紧算子，所以由定理5和文献［2］中的命题2．9可以得到以下结论:

推论1 T(t)是X的拟紧算子．

引理3 0是A+B+E的几何重数为1的特征值．

证明 与文献［6］的方法类似，故略．

易证X的共轭空间X*为

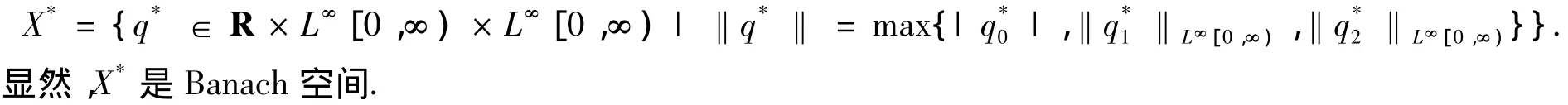
引理4 A+B+E的共轭算子(A+B+E)*为

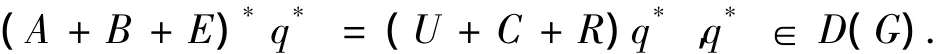
其中:

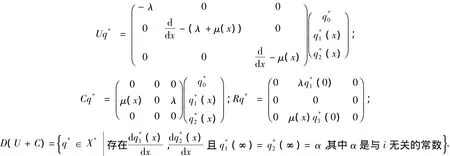
证明 与文献［6］的方法类似，故略．

引理5 0是(A+B+E)*的几何重数为1的特征值．

证明 与文献［6］的方法类似，故略．

由文献［6］的结论可得以下引理6、引理7．

引理6 0是A+B+E的代数重数为1的特征值．

引理7 0是(A+B+E)*的代数重数为1的特征值．

结合引理 3、定理1、推论1 及文献［2］中的命题2．9、定理 2．10，得

证明 利用定理5及文献［2］中的定理2．10可得

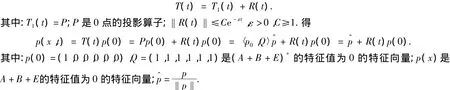
因此，系统解的指数渐近稳定性就得到证明．

［1］曹晋华，程侃．可靠性数学引论［M］．北京:高等教育出版社，2006:273-278．

［2］Nagel R．One-parameter semigroups of positive operators［M］．New York:Spring-Verlag，1986．

［3］Webb G F．Theory of non-linear age-dependent population dynamics［M］．New York:Marcel Dekker，1985．

［4］艾尼·吾甫尔．一类Banach空间中列紧集的描述［J］．新疆大学学报:自然科学版，2005，22(4):389-392．

［5］Gupur G，Li Xuezhi，Zhu Guangtian．Functional analysis method in queueing theory［M］．Hertfordshire:Research Information Ltd，2001．

［6］Shen Zifei，Hu Xiaoxiao，Fan Weifeng．Exponential asymptotic property of a parallel repairable system with warm standby under common-cause failure［J］．Journal of Mathematical Analysis and Applications，2008，341(1):457-466．