带权决策表的变精度约简算法

李 旭,荣梓景

(北京语言大学 信息科学学院,北京 100083)E-mail:1165297698@qq.com

1 引 言

粗糙集理论[1]是由波兰学者Pawlak提出的,是一种处理不确定、不一致和模糊问题的数学分析工具.近年来,粗糙集理论的研究成果丰硕,在机器学习、数据挖掘、决策支持与分析、医疗卫生服务、物联网等诸多领域中,取得了成功的应用.由于经典的粗糙集对分类误差敏感,使其应用受到了很大程度的限制而降低了分类预测能力.为了克服经典粗糙集模型的这种局限性,变精度模型[2]引入概率后,增强了模型的抗噪性,可以更有效得处理数据分类,因而推进了粗糙集理论的研究,并且拓宽了粗糙集理论的应用领域.

属性约简是粗糙集理论研究的重要内容,其主要思想就是根据特定规则要求,删除冗余和不相关属性,构成知识分类最小属性集.许多学者对正区域约简、变精度粗糙集模型进行了深入研究,在经典粗糙集模型约简中,二元关系是等价关系,为了更好处理信息丢失的决策表,已有研究通过容差关系[3]、相似关系[4]、量化容差关系[5]、限制容差关系[6]拓展了粗糙集约简研究.目前,Liu[7]在一致决策表和不一致决策表上提出了一般关系,从而推广了决策表中的二元关系,并研究了关系决策系统上的属性约简.文献[8]用一般关系给出了正区域约简的概念及相应的辨识矩阵,并给出严格证明.文献[9]在变精度模型下讨论了7种不同形式的约简,进一步阐述了变精度模型和经典粗糙集模型的差异.文献[10]通过概括了变精度模型的定义,同时,以矩阵的观点提出了变精度模型的上下近似.文献[11]中,当决策属性满足自反性时,证明了关系决策系统的分布约简等于关系系统的约简.文献[12]通过计算条件属性的重要度,运用启发式算法得到属性约简.文献[13,14]给出了变精度约简模型中分布约简、最大分布约简和分配约简的概念,以及所对应的辨识矩阵,并给出了辨识矩阵的严格证明.文献[15]提出了变精度约简中局部约简的概念,以及对应的辨识矩阵,并给出了严格证明.文献[16]在变精度模型下,研究参数的关系对于对象分类的影响.文献[17]基于矩阵观点,提出了绝对约简、分布约简、正区域约简这三种约简统一的不变矩阵的概念.通过建立不变矩阵统一约简算法来处理三种不同的约简.此外,研究人员还提出了不同类型的属性约简.例如,覆盖约简[18,19]、代价敏感度约简[20].现有属性约简研究主要针对不同背景的实际问题,对粗糙集进行属性约简,而缺少对于不同属性约简之间相互联系的研究.由于变精度约简和正区域约简是决策表中两种重要的约简类型.因此,研究变精度约简和正区域约简之间的联系是有意义的.

本文提出了带权决策表的概念并研究了带权决策表中变精度约简方法.在带权决策表中,通过对变精度约简和正区域约简进一步比较研究中,当精度阈值大于0.5时,给出了一种经适当更改部分对象的决策值后得到新的决策表的具体方法,该方法虽然使得原有的决策规则发生改变,但此时,带权决策表中的变精度约简可以转化为新的决策表中的正区域约简,并给出了两者对应的辨识矩阵等价证明,从而提出了一种关于变精度约简转化为正区域约简的具体算法.本文所提出的算法简化了原来的计算过程.

本文结构组织如下:第2节回顾了粗糙集中的基本概念、正区域约简定义及其对应的辨识矩阵.第3节提出了带权的决策表模型,给出了带权决策表中的变精度约简及其相应的辨识矩阵.第4节,当精度阈值大于0.5时,提出了一种变精度约简转化为正区域约简的具体转化算法,并给出了理论证明.第5节通过举例分验证了算法的有效性.

2 基本概念

本节主要回顾了正区域约简以及其对应的辨识矩阵.属性约简主要是通过辨识矩阵算法或者启发式算法实现的,启发式算法虽然能够得到约简,但往往不能得到所有约简.基于辨识矩阵的约简方法的数学论证严格,能够得到所有约简,目前仍是得到所有约简的最好方法.因此,本文所涉及的属性约简是在辨识矩阵[21,22]的基础上实现的,通过得到辨识函数,将其从合取范式转换为析取范式,从而得到全部约简.

定义3.若X⊆U,对于∀x∈U,定义关于X的特征函数[7]λX(x)为:

(1)

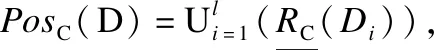
1)PosC(D)=PosB(D)Δ

(2)

2)若ø≠B′⊂C,PosC(D)≠PosB′(D)

(3)

称B是C关于D的正区域约简.

在计算正区域约简时,相应的辨识矩阵[8]为M=(mij)s×n:

(4)

在辨识矩阵M中,s=|PosC(D)|是正区域的基,n=|U|是论域中的元素数.

3 带权决策表的变精度约简

在决策表的基础上,通过引入权,本节提出了带权的决策表的概念,因而带权的决策表是对通常决策表概念的推广.并在带权决策表中,提出了变精度约简及其对应的辨识矩阵.

3.1 带权的决策表

在决策表中,若把决策表中的每一行作为一条决策规则,对于出现相同决策规则的次数称为权.本文假设所有的权值为正整数.这时给决策表增加一列来表示权,使得决策规则在决策表中出现的次数由权来表示,则称该决策表称为带权的决策表,用(U,C∪D,W)表示,其中,U是论域,C是条件属性集,D是决策属性集,W为对象的权,RC,RD分别是条件属性,决策属性在U上的等价关系.

例如,决策表(U,C∪D)(表1),其中,对象集U={ui|i=1,2,…,8},条件属性集C={a1,a2,a3},D是决策属性集.

表1 决策表Table 1 Decision table

例如,在条件等价类{u1,u2,u3,u4,u5}中,对象u1,u2,u3具有相同的决策规则,且该条规则共出现3次,我们给这条规则的权值赋为3.对象u4仅有1条决策规则,我们给这条规则的权值赋为1,对象u5仅有1条决策规则,我们给这条规则的权值赋为1.现对决策表(表1)增加权后,得到了带权的决策表(U,C∪D,W)(表2),其中,对象集U={xi|i=1,2,…,5},W为对象的权.

定义5.设(U,C∪D,W)为带权的决策表(定义同上),条件属性决定的等价类记为[x]C,当X⊆U时,定义:

(5)

定义6.设(U,C∪D,W)为带权的决策表(定义同上),条件属性决定的等价类记为[x]C,决策属性所确定的商集为U/D={D1,D2,…,Dl},对于∀x∈U,则记向量[10]为:

(6)

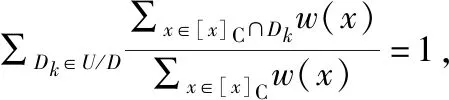
表2 带权的决策表Table 2 Weighted decision table

属性重要度[1,13]是衡量条件属性相对于决策属性依赖程度的度量指标,一般情况下,不同条件属性的重要度是不同的,条件属性的重要度越大,说明该条件属性相对于决策属性越重要,计算属性重要度对于条件属性具有重要意义,因此,我们基于带权的决策表提出了属性重要度.

定义7.设(U,C∪D,W)为带权的决策表(定义同上),x∈U,对于条件属性a∈C,其属性重要度为:

(7)

在带权的决策表中,条件属性重要度越大,说明该条件属性对正区域影响作用较大,反之,说明该条件属性对正区域影响作用较小.

3.2 带权决策表的变精度约简

在带权的决策表模型中,结合变精度约简[10,15],可以得到变精度约简对应的辨识矩阵.相比于决策表中的变精度约简对应的辨识矩阵,定义向量μCD(x)侧重于考虑条件类的元素个数.而在带权的决策表中,变精度约简对应的辨识矩阵,定义向量μCD(x)侧重于考虑条件类中元素的权值.

引理1.设(U,C∪D,W)为带权的决策表(定义同上),决策属性所确定的商集为U/D={D1,D2,…,Dl},当β∈[0,1]时,对于任意x∈U,μCD(x)的β截向量[15]如下:

(μCD(x))β=(λ(RC)(β)(D1),λ(RC)(β)(D2),…,

λ(RC)(β)(Dl))

(8)

引理2.设(U,C∪D,W)为带权的决策表(定义同上),当β∈[0,1]时,对于任意x∈U,μCD(x)的β截向量[15]如下:

(9)

定义8.设(U,C∪D,W)为带权的决策表(定义同上),Ø≠B⊆C,若B满足下列两条件:

1)对于∀x∈U,(μCD(x))β=(μBD(x))β

(10)

2)若Ø≠B′⊂B,∃x∈U,有(μCD(x))β≠(μB′D(x))β

(11)

称B是精度阈值为β的变精度约简[15,17].

(12)

其中,在辨识矩阵M(β)中,n=|U|表示论域中的元素数.由公式(12)知,对于任意精度阈值β1,β2,其相应所得的约简结果可能不相同.

1)(μCD(x))β=(μBD(x))β

(13)

(14)

(15)

在带权的决策表中,精度阈值为1的变精度约简对应的辨识矩阵和正区域约简对应的辨识矩阵等价[17],因而可得相同约简.

4 带权决策表的变精度约简与正区域约简

相比正区域约简,变精度约简计算过程相对复杂.当精度阈值β大于0.5时,我们发现变精度约简可以转化为正区域约简进行计算.因而本节提出了在带权决策表上更改某些(个)等价类[x]C中部分对象决策值的具体方法,从而得到新决策表(该定义由4.1节知).同时,证明了在带权决策表中的变精度约简等于新决策表中的正区域约简.

4.1 带权的决策表转化过程

在新的带权决策表(U′,C∪D′,W′)中,条件属性在U′上的等价关系不变,但改变了部分对象的决策值,使得决策属性在U′上的等价关系发生了改变.因此,相比于带权的决策表,新的带权决策表中不同的决策规则数量减少了,则对象的权值也随之发生改变.

例如,(U,C∪D,W)(表3)是带权的决策表,U={xi|i=1,2,…,7},条件属性集C={a1,a2,a3},决策属性集D,W为对象的权.现取精度阈值β=0.6.

表3 带权的决策表Table 3 Weighted decision table

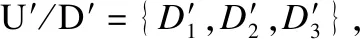
表4 新的带权决策表Table 4 New weighted decision table

显然,当任意条件等价类中所有对象具有相同决策规则时,即在新的带权决策表中,任意条件等价类仅有一条决策规则时,该类属于正区域集合.反之,任意条件等价类有两条及以上的决策规则时,该类不属于正区域集合.

由第2节所给的正区域约简对应的辨识矩阵可知,正区域约简时,新的带权决策表中的权不起作用,因此可以删除对象的权,得到新的决策表(U′,C∪D′)(表5).

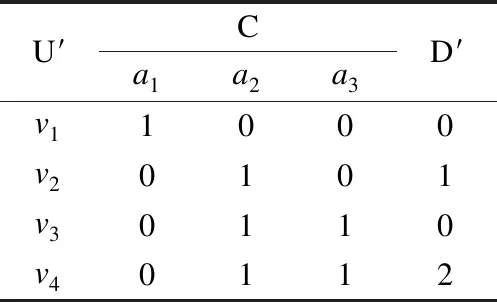
表5 新决策表Table 5 New decision table

本文要求精度阈值β大于0.5,主要考虑两个方面:阈值取值越大时,虽然提取规则的确定性越强,但容错性也越低.当精度阈值小于等于0.5时,一般认为是不可信的;若任意条件类的精度阈值β均小于等于0.5时,会出现多个决策值满足要求,则本节所提出的转化过程无法改变决策值,因而4.2节中定理2不成立.为保持一定程度的规则可信度和容错性,精度阈值的取值须大于0.5.例如,(U,C∪D,W)(表6)是带权的决策表,U={xi|i=1,2,…,5},条件属性集C={a1,a2,a3},决策属性集D,W为对象的权.

表6 带权的决策表Table 6 Weighted decision table

由表6知,商集U/C={{x1,x2,x3},{x4,x5}},商集U/D={D1,D2,D3},其中,D1={x1},D2={x2,x5},D3={x3,x4}.若取精度阈值β=0.3时,在条件类[x1]C={x1,x2,x3}中,该类中有P(D1|[x1]C)=0.4≥β,P(D2|[x1]C)=0.4≥β,按照本节提出的转化方法,无法改变条件类[x1]C中任意对象的决策值;在条件类[x4]C={x4,x5}中,该类中有P(D2|[x4]C)=0.5≥β,P(D3|[x4]C)=0.5≥β,按照本节提出的转化方法,无法改变条件类[x4]C中任意对象的决策值;则表6中的正区域是空集,表6的变精度约简不能转化成正区域约简进行计算.所以需令精度阈值大于0.5.

4.2 带权的决策表中变精度约简与正区域约简的关系

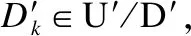
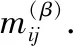
由3.2节知,辨识矩阵(4)和辨识矩阵(15)是正区域约简的两种等价的形式,其中,辨识矩阵(4)计算正区域约简时不需要考虑决策表的权.因此,由定理2知,在带权的决策表(U,C∪D,W)中,当精度阈值大于0.5时,变精度约简对应的辨识矩阵等价于新决策表(U′,C∪D′)中正区域约简的辨识矩阵(4),因而可得相同约简.本文提出算法1.

算法1.带权决策表中精度阈值大于0.5的变精度约简算法

输入:β∈(0.5,1],带权的决策表(U,C∪D,W)

输出:变精度约简

2)计算新的决策表(U′,C∪D′)中的正区域约简的辨识矩阵M=(mij)s×n;

3)构造辨识函数f=∏(∑mij≠Ømij),并把辨识函数f从合取范式转化为析取范式的形式;

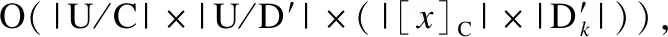
比较看来,算法1和变精度约简算法的时间复杂度区别于构建辨识矩阵的过程,其他步骤的时间复杂度相同.变精度约简算法构建辨识矩阵的时间复杂度O(|C|×|U|2),而算法1构建辨识矩阵的复杂度为O((|PosC(D′)|)×|U|×|C|),其中|PosC(D′)|<|U|,因此,算法1在一定程度上优化了时间复杂度.

5 实例分析

为了说明本文的算法,分别用变精度约简(记WVPR算法)和算法1对表3进行实例分析,例如,U={xi|i=1,2,…,7}代表导致不同机械故障的7种情况,C={a1,a2,a3}分别代表动力系统、供电系统、冷却系统,其中,“1”表示系统运行正常,“0”表示系统运行出现问题;D为决策集表示故障类型,其中,“0”表示故障F1,“1”表示故障F2,“2”表示故障F3;W为机械出现某种情况时发生故障的频次.

根据3.2节给出的辨识矩阵(12),因在4.1节中,取精度阈值β=0.6,则其变精度约简对应的7×7辨识矩阵为:

根据该7×7的辨识矩阵,可构造其分辨函数f=(a1+a2)(a1+a2+a3)(a3),通过合取范式为转化为析取范式,可得f=(a1a3)+(a2a3),则约简为{a1,a3},{a2,a3}.

当取精度阈值β=0.6时,因满足β∈(0.5,1],现用算法1对带权的决策表(表3)进行约简.表3经过转化后得到新的决策表(U′,C∪D′)(表5),对于条件等价类{v3,v4}中,对象v3,对象v4有不同的决策规则,由正区域定义知,PosC(D′)={v1,v2},根据公式(4),则正区域约简对应的2×4辨识矩阵为:

根据上述2×4的辨识矩阵,可构造分辨函数f=(a1+a2)(a1+a2+a3)(a3),通过合取范式为转化为析取范式,可得f=(a1a3)+(a2a3),则约简为{a1a3},{a2,a3}.

表3中,由辨识矩阵(12),取精度阈值β=0.65,则其变精度约简对应的7×7辨识矩阵为:

根据该7×7的辨识矩阵,可构造其分辨函数f=(a1+a2)(a3),通过合取范式为转化为析取范式,可得f=(a1a3)+(a2a3),则约简为{a1,a3},{a2,a3}.

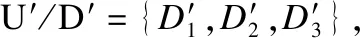
表7 新决策表Table 7 New decision table

PosC(D′)={v4},根据公式(4),则正区域约简对应的1×6辨识矩阵为:

[{a1,a2} ø {a1,a2} ø {a3} {a3}]

根据上述1×6辨识矩阵,可构造分辨函数f=(a1+a2)(a3),通过合取范式为转化为析取范式,可得f=(a1a3)+(a2a3),则约简为{a1,a3},{a2,a3}.

显然,运用两种算法对决策表进行约简时,所得结果相同,说明本文的算法是可行的.需要说明的是,不同的精度阈值的变精度约简得到的约简可能不同.

表8 数据集中的有关信息Table 8 Relevant information in data sets

为进一步说明算法,本文从UCI数据集中选取了3个数据集(Wine,Thoracic Surgery,Vehicle Silhouettes)(表8),对WVPR算法和算法1进行比较.程序运行环境:Intel(R)Core(TM)i5-2440 CPU 3.10GHz,Windows10 64bits.算法为Python代码实现.

现取β=0.7时,因为满足β∈(0.5,1]时,精度阈值为0.7的变精度约简可以转化为正区域约简进行计算.表9是两种算法分别在3个数据集上所得到的约简,两种算法所得约简结果相同.

表9 两种算法约简对比Table 9 Comparisons of two reduction algorithms

表10是算法在不同规模的数据集上运行所需的时间.本文提出的算法运行时间优于WVPR算法的运行时间.

表10 两种算法约简时间Table 10 Reduction time of two algorithms

通过实验说明:在带权的决策表中,当变精度约简的精度阈值β∈(0.5,1]时,可由算法1进行计算,且该算法一定程度上提高了运算效率.

粗糙集对通常的决策表进行处理时,无需任何先验知识或信息.带权的决策表通过引入权的概念,为决策表提供了先验知识或附加信息,因而提出了在该表中的变精度约简问题.相对于带权决策表中的变精度约简,本文所提算法能够在更少时间得到全部约简.此外,该算法可应用在智能诊疗,事故应急决策等领域.

6 结束语

本文首先在决策表的基础上,考虑相同决策规则出现的次数,通过对决策表中的对象赋权值,提出了带权的决策表,并给出了该表中的变精度约简对应的辨识矩阵.其次,若精度阈值满足大于0.5的特定条件时,通过改变某些(个)条件类中部分对象的决策值,可得到新的决策表.同时,证明了带权决策表中的变精度约简和新决策表中正区域约简相等,从而提出了满足特定精度阈值时,变精度约简转化为关于新决策表中正区域约简的具体算法.相较于变精度约简,本文所提算法能够在更少时间得到约简.最后,通过实验说明了本文提出算法的可行性和有效性.在之后的工作中,我们将致力于解决非等价关系(相似关系、容差关系等)基础上的带权决策表中属性约简问题.