基于海面脉冲回波数据的散射系数获取方法

2012-12-03李炳槐童广德梁子长

制导与引信 2012年3期

李炳槐，童广德，梁子长

（电磁散射重点实验室，上海200438）

0 引言

反舰导弹、作战飞机、武装直升机等掠海低空目标往往处于复杂的海面背景环境中，利用海杂波影响雷达的目标检测性能，从而达到隐蔽自身的目的［1－4］。因此，获取海面环境实际电磁散射特性数据是深入了解海面电磁散射特性，加强新一代防御系统的抗海杂波能力的重要手段。目前，仿真海面散射系数的手段多为先采用各种功率谱函数如 PM 谱、JONSWAP谱、D－B－J谱等，或分形粗糙面模拟海面，再用数值方法（如 Mo M）求解模拟海面上的散射场积分方程得到散射系数［5－9］，其准确性取决于所用海面模型的可靠性。除了仿真手段，一些研究机构和研究人员还用雷达对海面做了大量观测并进行细致的统计分析，获取了不同入射角情况下的海面散射系数［10－14］。

本文对挂载在飞机上的测试雷达采集到的海面脉冲回波数据提取出海面散射回波电压，根据雷达脉冲参数和天线的增益，用网格划分方法计算加权的海面有效面积。再统计出天线接收到的海面回波平均功率，最后求出一定入射角范围内的海面散射系数，与一些前人的测量结果基本一致。

1 脉冲雷达测试方法

海面散射系数测量采用挂飞方式，将测试雷达置于飞机底部。雷达天线以不同倾角照射海面，获取大面积海域动态的海面散射系数。测试雷达采用脉冲体制，发射脉宽为τ，重复周期为T，时序如图1所示。海面回波信号经过接收机的放大后，被采集器记录成数据文件，其中接收机的接收波门避开发射脉冲。

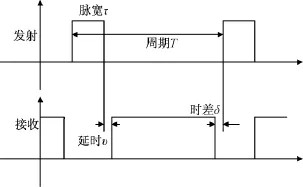
图1 测试雷达时序图

雷达发射脉冲为高频正弦信号，接收信号经过散射回波的幅度调制，即提取接收信号的包络可得散射回波电压。在发射脉冲的持续时间内，一部分发射脉冲会泄露到接收机内，使采集器记录数据的幅度较大，因此对发射脉冲持续时间内的接收信号不予处理。

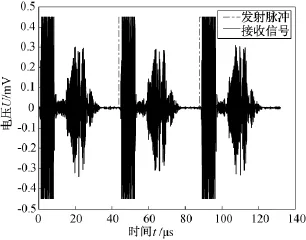
图2天线俯仰角为 30°时的多个周期的发射脉冲和接收信号电压

2 基于海面脉冲回波测量数据的散射系数获取方法

接收功率Pr与雷达散射截面σ的关系如下：

式中：Pt为发射功率；λ为波长；Gt、Gr分别为发射、接收天线的增益；R为天线到海面照射点的距离。因天线为收发并用，故Gt＝Gr＝G。σ与散射系数σ0的关系如下：

式中：S为天线波束照射到海面的面积。由于天线发出的是3 dB宽度为5°的圆锥形波束且有一定的俯仰角，故波束照射到海面的区域为一个椭圆。假设天线在海面的投影为O点，按照到天线距离的不同，该椭圆可被划分成若干个以O点为圆心的同心细圆环，如图3所示。划分的原则为相邻两个细圆环到天线的距离差ΔR＝cΔt／2，其中c为电磁波的传播速度；Δt为采集器记录的相邻两个采样数据点的时间差，即采样频率的倒数。入射角θ＝cos－1（H／R），为电磁波入射方向与海面法线的夹角。因同一个细圆环上的点到天线的距离相等，故照射到同一个细圆环上的电磁波的入射角相等。

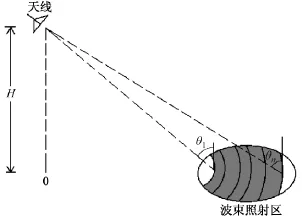
图3 天线与波束照射区示意图

以发射脉冲的上升沿作为一个周期的时间零点，由于发射脉冲具有一定的持续时间τ，则该周期内的时刻t天线接收到的回波信号实际是来源于波束照射区中的连续若干个细圆环的散射（如图3中的阴影部分所示）。在时刻t的接收功率Pr（t）有贡献的细圆环个数n与脉宽τ的关系如下：

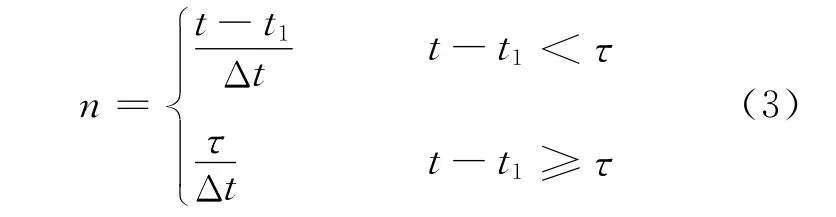
式中：t1为t所在的周期内天线刚好开始接收到海面散射回波的时刻。设第i个细圆环对应的入射角为θi，则这些细圆环对应的入射角范围为θ1～θn，其中θn＝cos－1（2 H ／ct），θ1与τ的关系如下

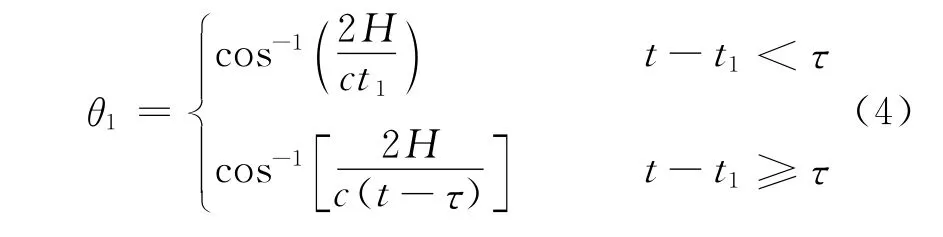
Pr（t）可表示为

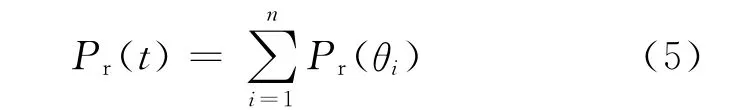
式中：Pr（θi）为第i个细圆环贡献的散射回波功率。根据式（1）和式（2），Pr（θi）可表示为

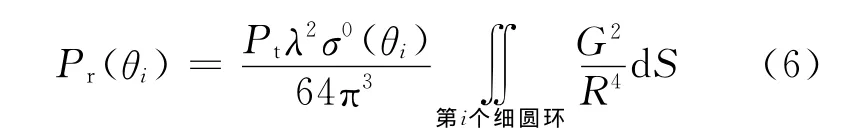
式中：σ0（θi）为入射角θi对应的海面散射系数；可理解为权函数为天线增益平方G2除以距离四次方R4的第i个细圆环的加权面积。由于天线的增益会随着与波束中心夹角的变化而变化，而同一个细圆环上的点与天线之间的连线和波束中心的夹角是不一样的，因此为了求出细圆环的加权面积，需要把细圆环再划分成一个个小面元，如图4所示。每个面元实际上是角度很小的圆环（扇形），仍以O点为圆心。

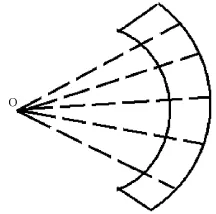
图4 细圆环内划分面元示意图

某个面元的加权面积近似为该面元的面积乘以对应的G2再除以R4。对同一个细圆环内的所有面元的近似加权面积求和，可近似得到该细圆环的加权面积。面元划分得越小，得到的细圆环加权面积就越精确。

若θ1与θn相差较小，根据式（5）和式（6），Pr（t）可近似为

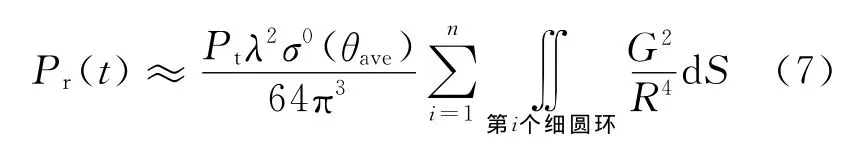
式中：θave＝（θ1＋θn）／2，是对Pr（t）有贡献的n个细圆环对应的平均入射角。先算出n个细圆环的加权面积的总和，再根据Pr（t）和已知的发射功率、波长等参数，即可求出散射系数σ0（θave）。

在飞机飞行的过程中，由于海面状况是随机起伏的，天线在不同周期内接收到的海面回波信号也会随机变化，故需要通过统计大量周期的接收信号得到其平均值。对天线俯仰角为－30°时记录的数据文件，每隔一千个周期提取一个周期的电压信号，取信号包络后再统计得到一个周期的平均接收功率Pr与时间的关系如图5所示。其余天线俯仰角时的一个周期的统计平均接收功率也按照上述方法处理得到。

3 海面散射系数处理结果

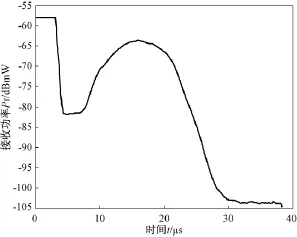
图5 天线俯仰角为－30°时的一个周期的统计平均接收功率

按照上述算法对天线俯仰角为－30°时记录的数据文件处理，可得到入射角为55°～60°范围内的一段海面散射系数曲线。用同样的方法处理天线俯仰角分别为－20°、－10°时采集到的数据，可获取入射角分别在60°～67°、70°～75°的范围内海面散射系数与入射角的关系曲线。将这三段曲线拼接起来，如图6所示。因天线俯仰角为－20°时，挂飞试验采集到的入射角大于67°的海面回波数据正好落在下一个周期的发射脉冲的持续时间内，无法处理，故图6中的海面散射系数曲线在入射角为67°～70°范围内出现了空缺。

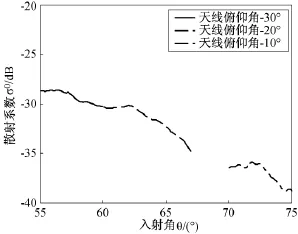
图6 海面散射系数与入射角的关系

从图6可以看出，随着入射角的增加，海面散射系数呈现逐渐减小的趋势。当入射角为60°时，海面散射系数约为－30 dB，而当入射角为75°时则约为－39 dB。这与 Merrill I．Skolnik主编的《雷达手册》中Masuko等人的机载测量结果、美国海军研究实验室的NRL－4FR雷达数据、Skolnik和Nathanson对早期测量数据的总结比较一致［10］。

4 结论

本文对挂飞试验采集到的海面脉冲回波数据进行了处理，根据接收到的海面散射回波统计平均功率，并计算加权海面散射面积，获取一定入射角范围内的海面散射系数。处理结果与一些前人的测量数据比较一致，这说明本文的脉冲体制测量方法、散射回波功率统计平均方法及加权散射面积计算方法有效可行，有助于今后的海面环境电磁散射理论研究。

［1］蔡红豪，王晓冰，薛正国，等．海环境实验室模拟及电磁散射测量技术［J］．制导与引信，2009，30（2）：1－6．

［2］陈鲲，陈云秋，陈世友．海杂波建模与仿真［J］．舰船电子工程，2009，29（2）：95－98．

［3］崔嵩，李岩，郑昌．海面多路径效应对舰载雷达探测低空目标的影响［J］．舰船电子工程，2009，29（1）：104－106．

［4］方重华，宋东安，黄松高，等．海面散射对舰船编队电磁干扰影响的数学模型［J］．装备环境工程，2010，7（3）：71－74．

［5］闫沛文，童创明，邓发升．不同风速下海洋粗糙面散射系数的计算［J］．上海航天，2006，（4）：23－26．

［6］张平娟．粗糙海面与其上方目标的复合电磁散射研究［J］．安徽科技学院学报，2010，24（3）：19－21．

［7］姚纪欢．粗糙海面的电磁散射研究［D］．西安：西安电子科技大学，2000．

［8］方有培．海杂波特性研究［J］．上海航天，2002，19（5）：31－35．

［9］陈勇，侯德亭，张超，等．一维分形海面的电磁散射系数分析［J］．信息工程大学学报，2008，9（4）：498－500．

［10］ Merill I．Skolnik．雷达手册［M］．北京：电子工业出版社，2003．

［11］洪鹰，孙瀛，罗邦煦，等．岸基C波段和X波段雷达观测海面后向散射系数［J］．台湾海峡，1995，14（2）：187－194．

［12］董庆，郭华东，王长林．基于粗糙海面高度频谱函数的雷达后向散射系数计算［J］．遥感学报，2001，5（3）：171－176．