高频区金属球定标体RCS的近场修正

2012-12-03梁子长武亚君

制导与引信 2012年3期

关键词：近场波束宽度定标

梁子长，李鸣，岳慧，武亚君

（1．电磁散射重点实验室，上海200438；2．上海无线电设备研究所，上海200090）

0 引言

近距离电磁散射测量过程中，入射电磁波的等相位波前通常为非平面，且采用窄波束天线进行观测的情况也较为常见，这与满足远场条件的平面波照射下的散射情况有较大区别，因此需引入近远场电磁散射概念。目前，人们通常根据两方面的经验准则给出其分界线：

a）满足平面波相位近似条件，即目标区内入射电磁波的波前相位变化小于π／8；

b）满足均匀照射近似条件，即目标区内照射或接收天线的增益变化不大于0．5 dB［1］（也有文献取1．0 dB［2］）。

相应地，当采用相对法进行近场散射测量数据标定时，由于定标体近远场的RCS值存在一定差异，需要对定标体的理论RCS值进行近场修正［3，4］，以提高测试数据精度与置信度。文献［4］中给出了金属平板定标体在球面波及局部照射条件下的RCS近场修正，而金属球RCS的近场修正研究则较少。

本文主要采用FEKO软件多层快速多极子方法计算金属球目标在不同观测距离下的RCS，并结合高频渐进法分析其变化规律，给出了金属球目标在球面波及目标局部照射情况下的近场RCS拟合修正公式，该公式可直接应用于近场RCS的测量定标。

1 近场RCS的引入

由于通常的雷达散射截面（RCS）定义主要针对目标位于收发天线远场、入射电磁波等相位面为平面波的情况［5－7］，对定标体 RCS的近场修正与定量进行分析，引入文献［8］给出的广义RCS定义：根据电磁场叠加原理，入射电磁场均可分解为无限小理想电偶极子或磁偶极子辐射场的组合，若将理想偶极子作为散射问题中电磁波照射与接收的观测条件，则广义RCS定义为

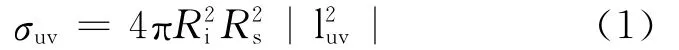
式中：u，v＝e，m，e表示照射及接收天线为电偶极子，m表示照射及接收天线为磁偶极子；Ri为照射偶极子与目标中心间的距离；Rs为接收偶极子与目标中心间的距离；l为散射复函数，该函数与目标散射特性、偶极子类型及指向等相关。以理想电偶极子观测天线为例，散射复函数l可写为

式中：λ为电磁波波长；Pv为表示接收电偶极子方向的单位矢量；Es为散射电场矢量；η为自由空间的波阻抗；I d l为照射电偶极子的强度。

对实际近场散射情况，可将发射和接收观测天线分别分解为一组偶极子天线，此时，根据场叠加原理，目标近场散射复函数可表示为各收发偶极子对散射复函数的矢量合成，目标近场RCS可类似采用式（1）给出。

2 高频区金属球的近场RCS修正

针对近场电磁散射的非平面等相位波前入射波与局部照射目标特征，计算分析在金属球目标在球面等相位波前入射波及窄波束天线观测情况下的近场RCS随距离等的变化规律。

2．1 金属球目标在球面等相位波前观测条件下的近场RCS

以半径分别为0．1 m和0．2 m的金属球为目标，观测天线设为理想偶极子，天线－目标观测距离为0．5 m～15 m，计算频段包含C、X、Ku和Ka。由于其在高频段的计算未知量较大，为提高计算效率，这里采用FEKO软件基于混合积分方程的多层快速多极子方法（MLFMM）进行计算。

同时，将金属球目标远场RCS与仿真计算的近场RCS相减，获得金属球目标的近场修正量，并将该值变换为金属球半径和观测距离的函数，得到两者间的函数关系，仿真结果如图1。其中图1（a）为数值计算得到的两不同半径金属球目标的近场修正量随距离的变化；将近场修正量变换为（R／a）－1．2的函数，其中R 为天线观测距离，a为金属球半径，则不同半径不同频率的金属球RCS近场修正量的变化如图1（b），由图可见，二者呈较好的线性变化关系。

为了进一步确认该变化趋势，通过高频渐进法分析金属球目标RCS与观测距离的函数关系。假定金属球半径为a，观测点至球心距离为R，其高频近似的近场散射复函数可写为

根据金属球自身遮挡作用，式中积分仅取可见的角度范围：θ1＝a cos（r／R）。高频渐进法计算的金属球近场 RCS随（R／a）－1．2的变化曲线如图2所示。

可见，高频渐进法结果进一步证实了金属球目标的近场 RCS与（R／a）－1．2间满足近似的线性递增关系，金属球近场RCS随观测距离减小而增加。在此基础上，对MLFMM计算结果进行拟合处理，则半径为a的金属球近场RCS（d Bm2）的近似计算公式写为

图1 金属球近场RCS修正量仿真结果

图2 高频渐进法计算的金属球近场RCS

图3则对比了式（6）拟合与MLFMM直接计算的金属球近场RCS结果，其频率为16 GHz，可见两者吻合较好。图3（a）为半径为0．1 m的金属球RCS结果，两者最大偏差为0．1 dB，图3（a）为半径为0．2 m的金属球RCS结果，最大偏差为0．3 dB。

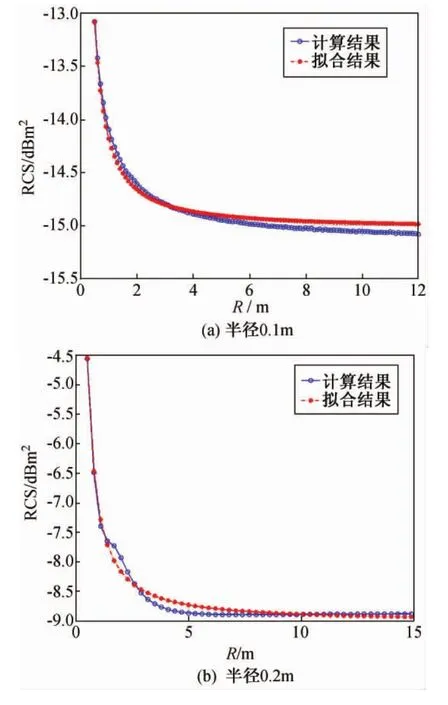
图3 金属球16GHz时近场RCS拟合结果比较

2．2 目标局部照射情况

近场散射问题中，目标被窄波束天线局部照射的情况较为常见，这里主要针对一维窄波束天线进行研究，假定天线主波束归一化远场方向图（单位为dB）满足：

式中：θ表示观测角，θ3dB为观测天线3 d B波束宽度。图4给出了该类天线近距离照射金属球（半径为0．2 m，波束宽度为4°）时其表面感应电流分布，可见，金属球表面上感应电流受到天线主波束照射范围的限制，其中电流较大的区域呈现为长条形，这将必然影响金属球的散射结果。

图4 窄波束天线局部照射下金属球感应电流分布

通过数值仿真计算，图5给出了不同频率、窄波束天线宽度及半径下金属球近场RCS随距离的变化。图5（a）中一维窄波束天线的3 dB波束宽度为4．0°，入射电磁波分别为 6 GHz、8 GHz、10 GHz、16 GHz和25 GHz，极化为 VV；图5（b）中入射电磁波频率为10 GHz，一维窄波束天线的－3 dB波束宽度分别为4．0°、4．8°、6．0°、7．8°和9．2°。图5（c）中入射电磁波频率为10 GHz，一维窄波束天线的3 dB波束宽度为4．0°，金属球半径分别为0．12 m、0．16 m、0．20 m、0．25 m和0．30 m。

由图5可见，金属球近场RCS随观测距离、频率、波束宽度及半径等参数的变化呈较强的规律性，其中近距离（约1 m以内范围）的起伏主要由天线旁瓣导致。当波束较宽或频率较高时，随着观测距离的减小，金属球近场RCS先增加后减少，且在几米观测距离范围内，金属球近场RCS的减小量随着波束变窄而增加。

这主要因为高频区内金属球的后向散射贡献来源于其镜面反射点附近的一小块区域，当距离较大时，其主要反射贡献区域仍被全照射，其变化仍符合球面波照射时规律而增加；而当观测距离进一步减小时，金属球主要反射贡献区域将被局部照射，且被照射区域面积随距离及波束宽度变窄而线性减小，对应地，其后向近场RCS也将快速减小。

对图5中不同情况下，同时利用公式（6）计算出其球面波观测下的近场RCS值，对两者差值（即窄波束天线观测引起的近场修正量）进行拟合，获得窄波束天线照射引起的近场RCS修正近似表达式（单位为d B）为

式中：θ3dB为观测天线3dB波束宽度；λ为入射电磁波波长；a为金属球半径；R为观测点至球心的距离（适用于约1 m以上观测距离）。

综合近似公式（6）和式（8），即同时考虑球面波及局部照射情况的金属球后向近场RCS可表示为

为验证式（9）的有效性，再次利用 MLFMM仿真计算其它半径或波束宽度情况下的金属球近场RCS，将其计算结果与式（9）近似结果进行比较，如图6所示。其中，图6（a）入射电磁波频率为16 GHz，波束宽度为 4．0°，金属球半径为0．25 m；图6（b）入射电磁波频率为20 GHz，波束宽度为6．0°，金属球半径为0．3 m；二者均吻合度较好，其最大偏差约为0．2 dB。