大锻件统计学t检验法的研究和应用
2012-09-25吕亚臣齐作玉于中海任运来
吕亚臣 齐作玉 于中海 任运来
(1.上海重型机器厂有限公司,上海 200245;2.上海电机学院, 上海 200240)
为了稳定控制和不断提升大锻件的产品质量,我们提出在大锻件生产领域中应用统计学理论,分析了以单件小批量生产为特征的大锻件生产领域里应用统计学的现状和困难[1、2]。同时,针对大锻件的单件小批量生产特点,给出了大锻件统计学Chi-square test的研究和应用实例[3]。至此,我们在难度极高的大锻件小样本统计学的研究应用上已经取得了一定的突破。
然而,Chi-square test所用的统计资料只是计数资料,其所对应的概率论中的变量也只是离散型的随机变量。我们在实际统计应用中遇到的变量通常是两大类,即离散型随机变量和连续型随机变量,它们所对应的统计学资料也是两个大类:即计数资料和计量资料。到目前为止,在大锻件小样本统计学的应用研究上,对离散型随机变量或计数资料的研究应用仅仅是起步,仍需要针对连续型随机变量或计量资料展开深入研究。
离散型随机变量或计数资料在实际应用中占据很大比重,它们是对每个观察单位用定量的方法测定某项指标所得的资料。这类资料大都是用测量工具或仪器测得的,带有度、量或其它单位,所以叫测量或计量资料,如抗拉强度、屈服强度、伸长率、收缩率、冲击功和硬度等。因此针对连续型随机变量或计量资料来研究大锻件小样本统计学是十分必要的。
根据大锻件的单件小批量生产特点和统计学的基本理论方法,本文论述了大锻件的小样本Student test,即t检验,并给出了具体应用示例。该方法可用于大锻件工艺参数的科学分析和生产验证,也可用于大锻件质量分析和判断,还可用于构建新一代大锻件工艺与产品质量控制系统,帮助实现稳定和提升大锻件工艺和产品质量的目的。
1 t检验法理论基础
1.1 可信区间
在统计抽样研究中进行数量分析和比较时,如果以样本均数来估计总体的均数则叫点估计值。点估计值属于就数论数。从科学的角度,我们不能对就数论数下结论,而应该对数量加以必要的统计处理再下结论。在科学研究中,通常用区间估计,即估计总体均数落在什么范围,我们把这种范围叫做均数的可信区间。
1.2 显著性检验
不可能将总体的全部个体都进行观察,只能从中抽取部分进行试验研究。用部分的研究结果说明总体规律性,这种方法叫做抽样调查。抽样调查的结果受到偶然现象的影响,所得结果与总体之间存在一定的差异叫作抽样误差。抽样误差总是存在于抽样调查之中,统计处理就是研究各数之差是不是由抽样误差引起的一种方法(所以也叫误差检验)。如果样本之间的差异是由抽样误差引起的,那么这些样本可能来自规律相同的总体,就其总体规律来说没有差异。如果各数间的差异不是由抽样误差引起的,那么这些样本可能不是来自一个总体,而是来自规律不同的两个或几个总体。也就是说,这些有差别的样本可能代表着几个不同的总体,所以差异显著。
统计上用概率P来表示由抽样误差引起的可能性有多大。习惯上将P≤0.05 或P≤0.01称为小概率事件,表示事件发生的可能性很小。统计学上习惯规定P>0.05为差异不显著,0.05≥P>0.01为差异显著,P≤0.01为差异非常显著。
1.3 t检验
t检验是根据t分布(标准正态分布)原理建立起来的显著性检验方法。
自由度为n的t分布的概率密度为[4]:
(1)
式中,-∞ 根据f(t)的图形,它关于t=0是对称的,并且形状类似于正态变量概率密度的图形。该图形适合于用小的自由度n或者小的样本量来表示。在t分布表格中,n通常也是比较小的数值,有些t表格只表示了最大为45的n值。n越大,t值的变化越小。 统计学研究的结果表明,我们应该根据所抽取样本量的大小来选择不同的显著性检验方法。通过对统计学方法的分析归纳,可以得出以下观点: 对于计量资料的显著性检验,当样本含量较小,比如200例以下,应该选用t(Student)检验;当样本含量大于200,则采用n→∞的标准正态分布的检验。 关于最小样本量,目前没有确切的要求,但原则是应该满足统计要求。比如,正态性检验,它适用于7~2 000的样本量。而根据t值和t分布的特征和各种统计学应用实例,样本量应该在6~200之间。 长轴类锻件轴端的力学性能在拔长比达到一定条件后容易出现各向异性,它们之间的比值称为异性系数。 20世纪80年代,上海重型机器厂为上海电机厂生产45钢电机轴时常常会碰到电机轴切向性能不能满足技术要求的问题。在对1987年的电机轴统计中发现,全年有39个锻件在试验检查中出现了切向力学性能不合格的问题。进一步的统计发现,39个不合格锻件中,轴端锻比大于10的占95%,切向断面收缩率不合格的占97%,延伸率不合格的占3%。 这是典型的各向异性问题,表现是轴端部拔长比过大。但是,钢锭必须经过镦粗拔长的变形过程,最后的成品必须是有细的轴颈。因此,锻造上根本不能回避大拔长比的问题。 为此,有研究者提出改善电机轴切向力学性能的根本性措施是:改进冶炼工艺,研究钢锭缺陷,发展冶炼铸锭技术,提高冶金质量[5]。 国内其它重机厂也同样碰到过类似的问题。到底靠冶炼能否解决长轴类锻件的轴端各向异性呢? 为了解决40A船用电机轴的各向异性问题,文献[6]统计计算了碱性电炉钢和电渣熔炼钢的各向异性系数,包括延伸率、断面收缩率和冲击值的各向异性系数。该文献最后只是对数据进行了经验性直观判断,并没有给出科学的分析判断。 1987年统计电机轴的数据时发现,通常只出现轴向断面收缩率不合格与延伸率不合格的情况,故本文只讨论延伸率和断面收缩率的t检验应用。 电炉钢与电渣钢的延伸率异向系数见表1。 采用两样本均数比较的t检验方法进行分析,给出分析结果。 延伸率统计数据经处理后得到表2。 延伸率各向异性系数的检验步骤如下: (1)建立假设和确定检验水准 H0: 电炉钢延伸率异性系数的总体均数μ1与电渣钢延伸率异性系数μ2相同,即μ1=μ2。 H1:μ1≠μ2。 表1 电炉钢与电渣钢的延伸率异向系数Table 1 Elongation anisotropy coefficients of electric furnace steel and electric slag steel 表2 电炉钢与电渣钢延伸率的各向异性系数Table 2 Elongation anisotropy coefficients of electric furnace steel and electric slag steel (2)计算t值 1)合并方差 s02=[∑X12-(∑X1)2/n1+∑X22- (∑X2)2/n2]/(n1+n2-2)=0.013 7 2)均数之差的标准误 S(m1-m2) = [s02(1/n1+1/n2)]1/2= 0.053 8 3)计算均数 m1=∑X1/n1=1.237 m2=∑X2/n2=1.091 4 4)计算t值 t=(m1-m2)/S(m1-m2)=4.047 7 (3)确定P值 自由度n′=n1+n2-2=17 按n′和t界值表,所以P<0.001。 (4)判定结果 按α=0.05准则,拒绝原假设,可以认为电炉钢延伸率异性系数的总体均数μ1与电渣钢延伸率异性系数μ2差异显著。 电炉钢与电渣钢的断面收缩率异向系数见表3。 断面收缩率统计数据经处理后得到表4。 收缩率各向异性系数的检验步骤如下: (1)建立假设和确定检验水准 H0: 电炉钢收缩率异性系数的总体均数μ1与电渣钢收缩率异性系数μ2相同,即μ1=μ2。 H1:μ1≠μ2。 (2)计算t值 1)合并方差 s02=0.034 0 2)均数之差的标准误 S(m1-m2) = 0.084 8 3)计算均数 m1=∑X1/n1=1.396 m2=∑X2/n2=0.972 2 4)计算t值 t=(m1-m2)/S(m1-m2)=5.000 5 (3)确定P值 自由度n′=n1+n2-2=17 表3 电炉钢与电渣钢的断面收缩率异向系数Table 3 Area reduction anisotropy coefficients of electric furnace steel and electric slag steel 表4 电炉钢与电渣钢断面收缩率的各向异性系数Table 4 Area reduction anisotropy coefficients of electric furnace steel and electric slag steel t=5.000 5 按n′和t界值表,所以P<0.001。 (4)判定结果 按α=0.05准则,拒绝原假设,可以认为电炉钢收缩率异性系数的总体均数μ1与电渣钢收缩率异性系数μ2差异显著。 根据以上统计学方法的检验计算可得出结论,采用电渣钢可解决长轴类锻件的各向异性问题。 大锻件小样本统计学的研究还有许多内容值得继续展开。大锻件小样本统计学是大锻件生产行业的一项关键共性技术,它的成果将广泛应用于整个大锻件行业或领域中。关键共性技术研发是一项长期的基础性工作。由于关键共性技术的研究难度大、周期长,效果也是多年后才能显现,较难受到企业的高度重视,已经成为制约我国大锻件产业持续健康发展的核心问题。加快大锻件生产行业关键共性技术的研究和发展,尚需国家、行业和国有大型企业的共同努力。 [1] 齐作玉.大锻件生产统计学方法与概念的探讨.大型铸锻件,2010,(5):38-41. [2] 吕亚臣,任运来,齐作玉.构建新一代大锻件工艺与质量控制系统. 大型铸锻件,2010,(6):42-45. [3] 齐作玉,吕亚臣,任运来.大锻件统计学Chi-square test的研究和应用.大型铸锻件,2011,(1):9-25. [4] 浙江大学数学系高等数学教研组编. 概率论与数理统计.第1版.北京:高等教育出版社,1979, 208-226. [5] 《大型锻件的生产》编写组编. 大型锻件的生产.第1版.北京:机械工业出版社,1978,30-41. [6] 李兆劲.电渣重熔对钢的各向异性的改善.大型铸锻件,1995,(2):28-32.2 t检验方法和实例
2.1 长轴类锻件不合格原因分析
2.2 延伸率t检验应用
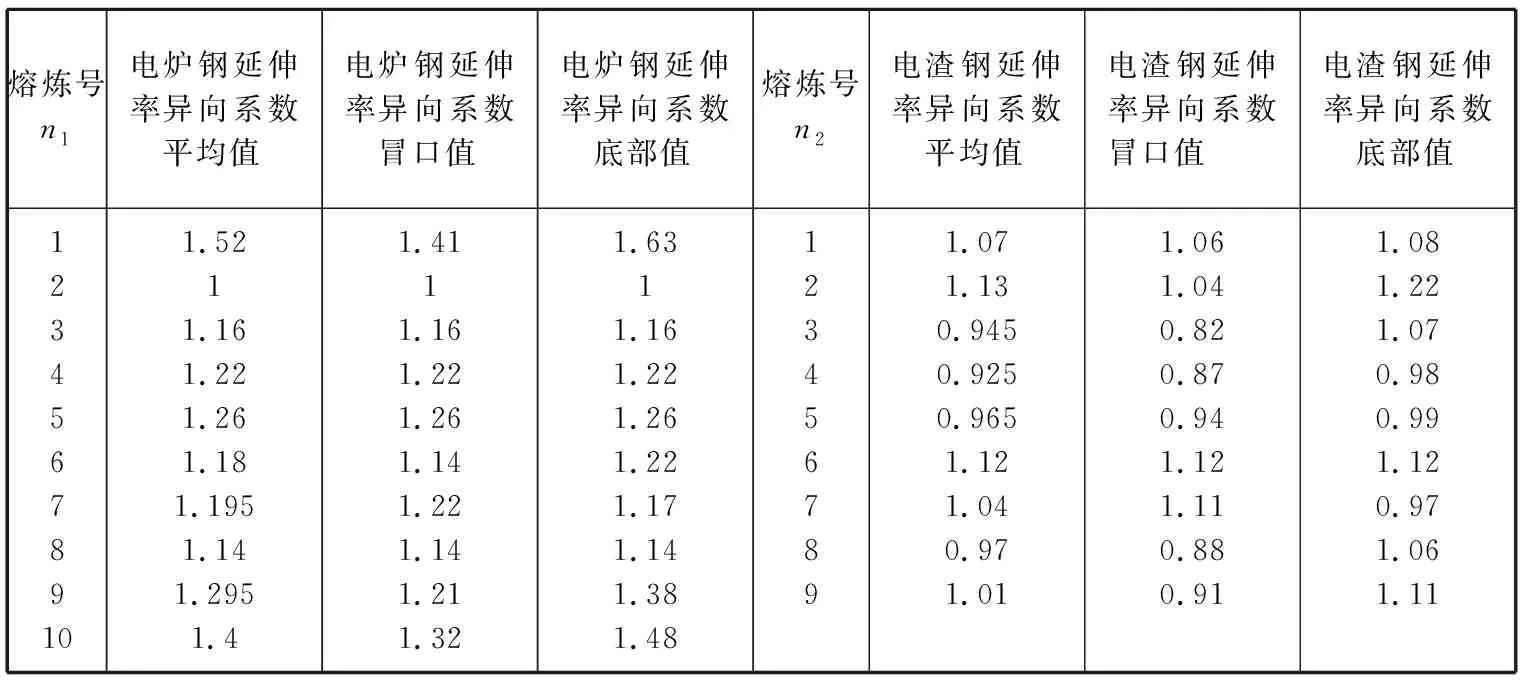
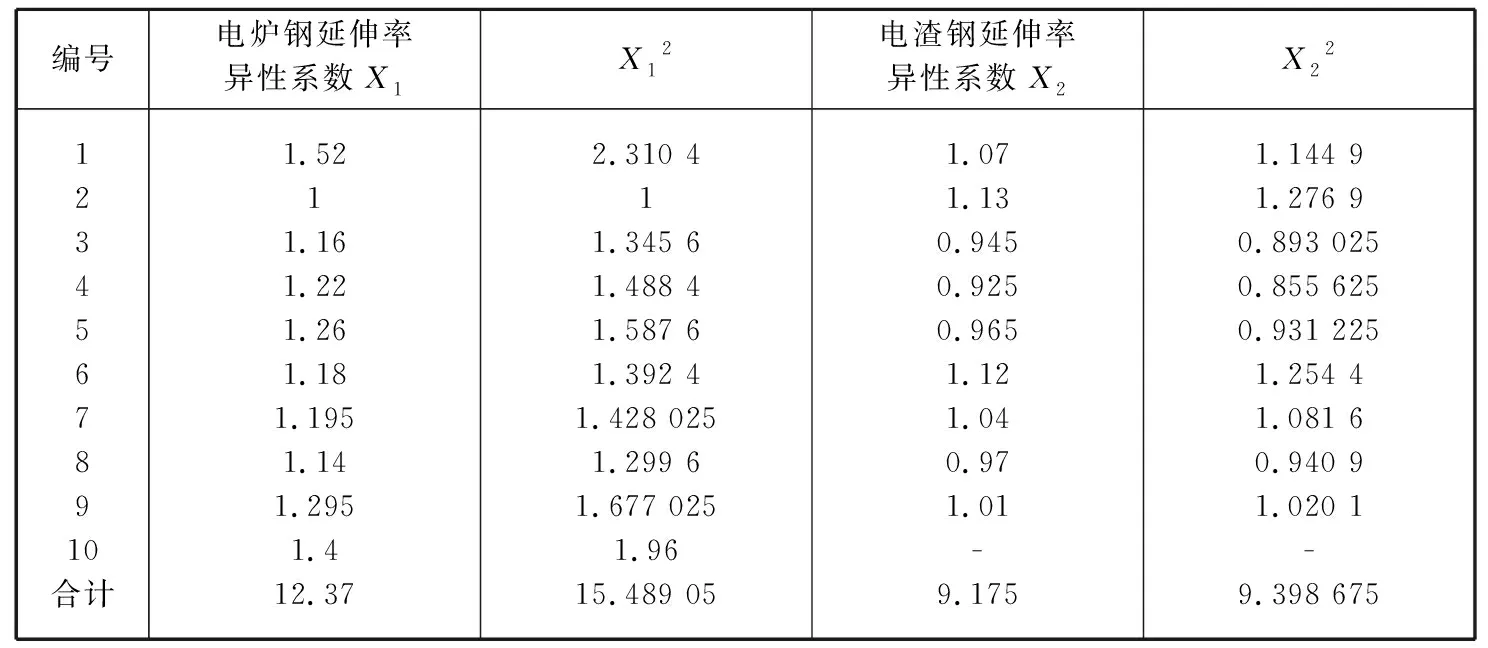
2.3 断面收缩率t检验应用电炉钢与电渣钢的断面


3 结束语
