双螺带螺杆桨气液混合性能数值模拟及其工业应用

张敏革，张吕鸿，姜 斌, ，葛 春，李鑫钢,

(1. 天津大学化工学院，天津 300072；2. 天津大学精馏技术国家工程研究中心，天津 300072)

随着轻化工、食品以及三大合成材料等工业的发展，高黏流体尤其是高黏非牛顿流体的搅拌混合操作日益增多[1]．高黏非牛顿流体的混合理论以及搅拌桨的设计、放大等均比牛顿型流体更为复杂．我国某油田公司三次采油中采用聚合物驱油技术提高原油采收率，这种聚合物溶液是一种高黏非牛顿流体[2-3]，其配制过程主要包括聚合物的分散、熟化以及外输等工序．分散工序将聚合物颗粒分散在水中；熟化工序主要通过搅拌装置来强化搅拌罐内聚合物与水的混合过程，加速聚合物的溶解，生成均匀混合溶液．在聚合物的熟化过程中，一方面需要防止搅拌槽内液体流动出现滞留死区，避免产生胶团；另一方面需要使聚合物充分接触并溶解完全，使混合液体成为密度和黏度均匀一致的高黏溶液．然而，聚合物在溶解过程中，本身由于水解反应产生部分气体，加上聚合物颗粒在分散过程中带入少量空气，熟化罐中溶液往往存在大量气泡，如果气泡不能很好地排出，溶液的均一度将下降，严重时将降低后序外输泵和注聚泵的供液能力，出现气蚀现象，影响泵的正常使用．

针对以上特殊情况，笔者开发了双螺带螺杆桨，这种搅拌桨在高黏非牛顿流体中的流场特征以及对溶液中气泡的作用效果是开发成功与否的关键．事实上，到目前为止，对于搅拌槽内气液两相流的研究大多数围绕六直叶涡轮桨或多层组合桨等径向流搅拌桨展开[4-6]，并且研究流体大部分为牛顿流体[7-8]，而对双螺带螺杆搅拌桨这种轴流式桨在高黏非牛顿流体气液两相流中的流场研究还鲜见相关报道．本文采用计算流体力学方法对双螺带螺杆桨气液两相流搅拌流场进行了数值模拟分析，并进行工业试验证实了这种搅拌桨应用于油田聚合物溶液配置过程中的适用性．

1 搅拌桨几何结构

图 1所示为双螺带螺杆搅拌装置结构示意图．搅拌槽模型为一平底圆柱型容器，直径为 D＝194,mm，高 H＝200,mm；从俯视图角度看，双螺带螺杆桨的外螺带为逆时针旋转，直径为 d＝160,mm；内螺杆为顺时针旋转，外螺带叶宽W1与内螺杆叶宽W2均为16,mm；螺带螺距为P＝160,mm，螺杆螺距Ps＝106.7,mm，桨高 L＝160,mm，螺带距槽壁的间隙 c＝17,mm．

图1 搅拌装置的几何结构Fig.1 Geometric structure of stirring apparatus

黏弹性流体搅拌流场的数值模拟计算困难很大，目前正处于起步阶段[9]．为简化计算、降低数值模拟计算的难度，本文忽略了聚合物溶液的弹性，搅拌槽内聚合物溶液的黏度用非牛顿流体模型幂律方程来表达[3]，其稠度系数为20,Pa·s，流变指数为0.75，密度为 1,000,kg/m3．

2 数学模型及数值求解方法

2.1 控制方程

采用双欧拉两相流模型对搅拌槽内气液流动进行数值模拟，即把搅拌槽内液相看成连续相，把气相看成拟连续相，用一套类似于连续液相的方程描述其特性，该方法适合于较多气泡或较大气量的气液两相流计算．对于不可压缩流体，该模型的具体表达形式如下所述．

相体积分率守恒方程为

连续性方程为

动量方程为

式中：下标g代表气相，l代表液相；Mgl为动量传递源项．这里动量传递源项主要考虑了气泡与液体之间的曳力，采用 Schiller and Naumann模型来表示，即

式中CD为曳力系数，

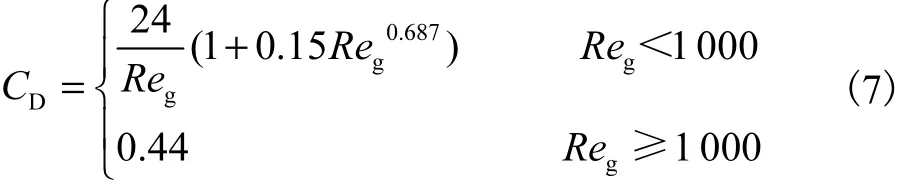
Reg为液相与气相的相对雷诺数，

研究表明[10-11]，这种模型在较大量气泡运动场中预测的平均气含率与试验值吻合较好．

2.2 网格划分

采用滑移网格法计算搅拌流场时，物理模型的网格划分需进行分区处理以便通过设置实现搅拌桨旋转运动，如图2所示．搅拌区域分为包含搅拌桨的Σ1和不包含搅拌桨区域的 Σ2，两部分区域的交界面为圆柱形；网格划分时桨带附近以及桨叶至槽壁采用六面体结构化网格，其余部分采用四面体非结构化网格；距离槽壁处划有由密到疏的网格边界层．网格划分并非越密越好，划分比较合理的网格会大幅度节省机时和内存，并且加快收敛速度．以桨叶表面平均剪切速率相对变化不大于 0.02为依据，确定网格总数为552,200个．

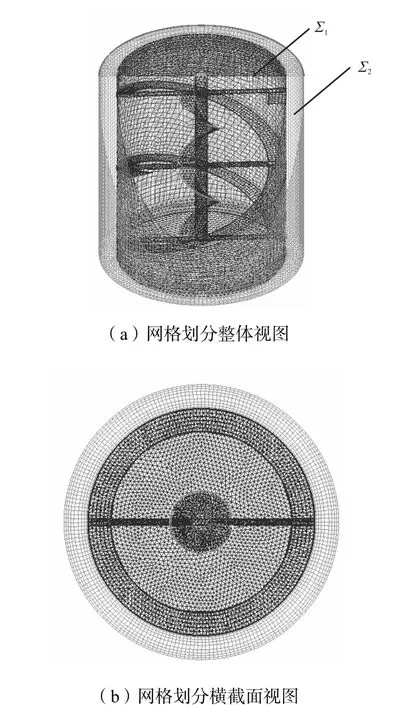
图2 计算区域网格划分情况Fig.2 Representation of mesh for calculational region

2.3 边界条件及初始条件

采用滑移网格法来处理运动的桨叶和其余槽体之间的相对运动．边界条件设置如下：

(1) 槽壁、槽底部以及搅拌桨表面为无滑移固体壁面；

(2) 搅拌槽液面为自由液面；

(3) Σ1区域旋转角速度与搅拌桨转速大小相等、方向相同；Σ2区域静止．

这样，方程(1)～(8)以及相应的边界条件就构成了描述气液两相搅拌流场的流体力学模型．计算时，壁面边界层采用标准函数处理，时间采用隐格式，对流项采用二阶迎风格式，压力-速度方程选用相间耦合的Simple方程，计算精度为10-3；时间步长设置为10-5,s；计算开始时，假定其搅拌槽内均匀分布着直径为 0.005,m的球形空气泡，气泡总体积占液相体积的10%，暂不考虑气泡的聚并与破碎．搅拌转速范围为45～70,r/min，搅拌雷诺数均在 100以下，属层流区范围．

3 模拟结果与讨论

3.1 搅拌流场速度分布

图3所示为搅拌流场达到稳态时y＝0截面液相速度矢量图．

从图中可以看出，外螺带和槽壁附近流体在桨叶的作用下一部分向槽底方向运动，一部分流体在螺带桨叶周围出现漩涡．这主要是因为搅拌桨在旋转过程中，在桨叶正面产生高压，而在桨叶背面产生低压，周围流体在这种压差的作用下向低压区流动，从而产生漩涡现象．流体到达槽底后向槽中心流动，螺杆附近及螺杆与螺带之间流体向上流动，到达液面附近后再由中心向槽壁流动，形成以轴向循环为特征的流场．总体来看，全槽速度分布比较均匀，尤其在槽底滞留区较少，有利于避免聚合物沉积而形成凝胶，使得混合时间延长，影响溶液均一化效果．

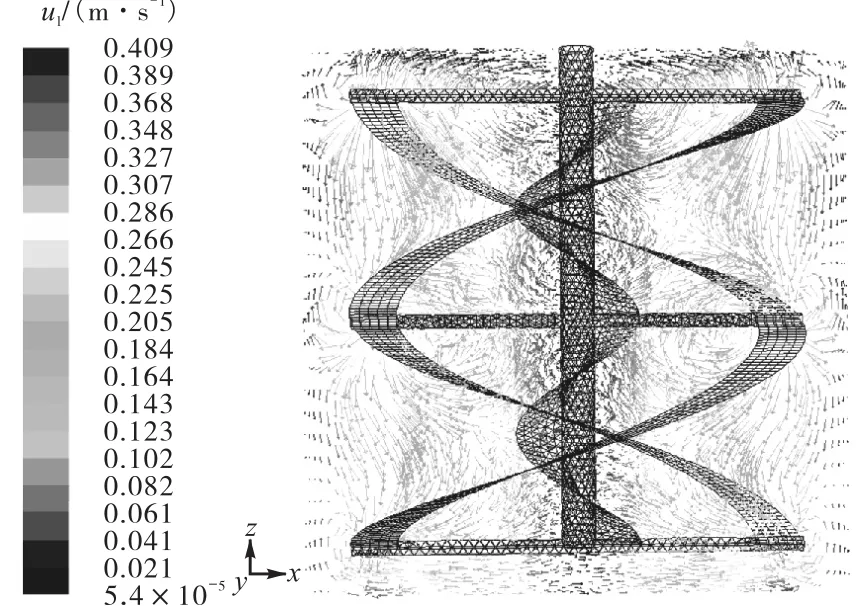
图3 y＝0截面速度场分布Fig.3 Velocity field distribution at y＝0,section

3.2 搅拌流场表观黏度分布

与牛顿流体不同，聚合物溶液的黏度并非一定值，而是随剪切速率的变化而变化，这里考察的聚合物溶液表观黏度与剪切速率呈幂律关系．为区别起见，聚合物溶液在一定的剪切速率下的黏度称为表观黏度．

图4所示为转速为45,r/min时搅拌流场x＝0截面的表观黏度分布．从图中可以看出，溶液在外螺带附近表观黏度最低，螺杆与螺带之间区域表观黏度稍大，说明流场中桨叶处剪切速率较大，螺杆及液面处剪切速率相对较小；在液面且靠近槽壁处黏度最大，为 19.7,Pa·s；而全槽平均表观黏度为 130,Pa·s，说明槽内表观黏度不均匀度较小，全槽表观黏度分布相对比较均匀．说明这种型式搅拌桨可使槽内流体受剪切而运动起来，有利于溶液中黏团的撕裂、分散和溶解，缩短溶液混合时间．

图4 x＝0截面表观黏度分布Fig.4 Apparent viscosity distribution at x=0,section

3.3 搅拌流场气含率分布

搅拌流场中的局部气含率可以充分地表征搅拌桨对槽内气体的作用．图5所示为双螺带螺杆桨转速为 60,r/min、逆时针旋转时，搅拌流场y＝0截面局部气含率在 0,s、0.6,s、3.5,s和 6.0,s时的分布情况．从图中可以看出，在考察的搅拌时间段内，搅拌槽中气液混合溶液受到搅拌桨的作用，在桨叶正面附近形成了液体富集，而在背面形成了气泡的富集．搅拌槽液面附近和搅拌槽底部气泡率先出现了液体富集区，这主要是因为搅拌槽液面附近气泡离液面距离很近，气泡在液体中所受的压力较小，在搅拌过程中气泡容易溢出，气含量较低；而槽底部流体出现液体富集的原因是搅拌桨叶对气泡汇聚作用；随着时间的推移，桨叶背面富集气体逐渐增多，最后气泡在桨叶背面形成气流通道沿桨叶向上流动，从而使搅拌槽底部的低气含率流体体积逐渐增大，搅拌槽内总体气含量逐渐减少．

图 6所示为搅拌桨转速为 45,r/min、60,r/min和70,r/min时搅拌槽内气含率随搅拌时间的变化规律，可以看出，约在 0～5,s内，搅拌槽内气含率变化较小，这期间气泡主要进行汇聚；随着时间的推移，搅拌槽内气含率逐渐减小；搅拌约 38,s后，气泡溢出率达 88.5%，基本实现了气泡在搅拌槽内逸出，搅拌槽内流体近似为均一液体．

双螺带螺杆桨的桨叶高度占搅拌槽总高度的比例较大，并且在高度区间内结构为连续的，这种结构型式的桨叶在搅拌过程中有利于气泡沿螺带和螺杆形成富集，产生螺旋式气流通道，促进气泡的快速排出．因此，双螺带螺杆搅拌桨可应用在对气-液两相混合溶液排除气相的场合．

图5 y＝0截面气含率分布Fig.5 Gas hold-up distribution at y＝0,section

图6 搅拌槽内气含率随时间变化规律Fig.6 Relationship between gas hold-up and time in stirred tank

4 工业验证及实施效果

在数值模拟过程中，气泡采用了直径大小相等而且在搅拌槽中均匀分布的假设，因此无法得到进行试验的初始条件，并且由于溶液的透明度差，采用目前最先进的PIV技术也无法获得气泡运动信息(可参见文献[12])．因此，本文对该型式搅拌桨进行工业放大，并在我国某油田三次采油厂进行了现场试验．

试验中熟化罐直径为 5.5,m，高为 5.5,m，装填系数为 0.80～0.90，双螺带螺杆搅拌桨的直径为4.5,m．在熟化罐中料液的浓度、温度、进料量均相同的条件下，与原来搅拌装置混合效果相比结果如表 1所示．

姜斌[3]对双层三叶桨的搅拌流场进行了数值模拟研究，发现双层搅拌桨的桨叶两面压力梯度较大，搅拌过程中易产生气蚀和空穴现象，不利于气泡的溶解和溢出．从表 1可以看出，与双层三叶桨相比，双螺带螺杆桨可使聚合物溶液的混合时间从原来的 4,h降低到2,h以内，虽然双螺带螺杆搅拌桨在单位时间内的功率消耗较大，但总能耗降低；搅拌混合 2,h以后，本课题组开发的双螺带螺杆桨搅拌槽中聚合物溶液基本没有胶团存在，溶液均一性较好，溶液中气泡较少，同时也验证了模拟分析预测的正确性；另一方面，采用新型搅拌桨后泵的维修周期大大延长，显著节约了运行费用；双螺带螺杆桨适合应用于三次采油地面工程中聚合物的水解混合过程．

表1 双螺带螺杆搅拌装置的运行效果Tab.1 Operation effect of double helical ribbon-screw impeller device

5 结 论

(1)双螺带螺杆桨使高黏气液两相流搅拌流场中的速度分布呈轴向大循环特征，流场中溶液表观黏度分布较均匀，这些均有利于聚合物黏团的分散、水解和混合．

(2)双螺带螺杆桨的自身的结构特点，可对溶液中气泡产生汇聚作用，引导气泡在桨叶处产生螺旋气流通道，加速气泡从搅拌槽溶液中溢出．

(3)工业试验表明，与双层三叶桨相比，双螺带螺杆搅拌桨对聚合物溶液的混合时间大大降低，均一化程度提高，能耗显著降低，适合应用于聚合物的水解混合过程．

符号说明：

c ——螺带距槽壁之间的间隙，mm；

CD——曳力系数；

d——螺带直径，mm；

D——搅拌槽直径，mm；

H——搅拌槽高度，mm；

L——搅拌桨高度，mm；

M——相间动量交换；

p——压力，Pa；

Ps——螺杆螺距，mm；

Rei——相对雷诺数；

S——传质源项；

t——时间，s；

u——速度矢量；

W1——螺带叶宽，mm；

W2——螺杆叶宽，mm.

α——相含率；

ρ——密度，kg/m3；

μ——动力黏度，Pa·s.

下标：

g——气,相；

l——液相.

［1］ 陈乙崇. 搅拌设备设计[M]. 上海：上海科学技术出版社，1985.

Chen Yichong. Design of Mixing Equipment[M]. Shanghai：Shanghai Scientific and Technical Publishers，1985(in Chinese).

［2］ Zhang Lühong，Zhang Dan，Jiang Bin. The rheological behavior of salt tolerant polyacrylamide solutions[J].Chemical Engineering and Technology，2006，29(3)：395-400.

［3］ 姜 斌. 新型聚合物水解搅拌装置应用研究及搅拌流场的数值模拟[D]. 天津：天津大学化工学院，2005.

Jiang Bin. Applied Study of New-Type Polymer Hydrolyzation Mixer and Numerical Simulation of Non-Newtonian Fluid in Stirred Tank[D]. Tianjin：School of Chemical Engineering and Technology，Tianjin University，2005(in Chinese).

［4］ Lane G L，Schwarz M P，Evans G M. Predicting gasliquid flow in a mechanically stirred tank[J]. Applied Mathematical Modeling，2002，26(2)：223-235.

［5］ Han Luchang，Liu Yuejin，Luo He′an. Numerical simulation of gas holdup distribution in a standard Rushton stirred tank using discrete particle method[J]. Chinese Journal of Chemical Engineering，2007，15(6)：808-813.

［6］ 宋月兰，高正明，李志鹏. 多层新型桨搅拌槽内气-液两相流动的实验与数值模拟[J]. 过程工程学报，2007，7(1)：24-28.

Song Yuelan，Gao Zhengming，Li Zhipeng. Experimental study and numerical simulation of gas-liquid flow in a stirred tank with a new multiple impeller [J]. The Chinese Journal of Process Engineering，2007，7(1)：24-28(in Chinese).

［7］ Jahoda M，Tomaskous L，Mostek M. CFD prediction of liquid homogenization in a gas-liquid stirred tank[J].Chemical Engineering Research and Design，2009，87(4A)：460-467.

［8］ Zhang Qinghua，Yong Yumei，Mao Zaisha，et al. Experimental determination and numerical simulation of mixing time in a gas-liquid stirred tank[J]. Chemical Engineering Science，2009，64(12)：2926-2933.

［9］ 张敏革，张吕鸿，姜 斌，等. 非牛顿流体搅拌流场的数值模拟研究进展[J]. 化工进展，2009，28(8)：1296-1301.

Zhang Minge，Zhang Lühong，Jiang Bin，et al. Progress in the numerical simulation for agitated flow field of non-Newtonian fluid[J]. Chemical Industry and Engineering Progress，2009，28(8)：1296-1301(in Chinese).

［10］ 孙 会. 搅拌罐内气液两相流场的数值研究[J]. 上海电机学院学报，2008，11(3)：189-192.

Sun Hui. Numerical investigation of gas-liquid flow in stirred vessels[J]. Journal of Shanghai Dianji University，2008，11(3)：189-192(in Chinese).

［11］ Law D，Battaglia F，Heindel T J. Model validation for low and high superficial gas velocity bubble column flows[J]. Chemical Engineering Science，2008，63(18)：4605-4616.

［12］ 张敏革. 超高分子量HPAM溶液流变行为与双螺带螺杆桨搅拌流场研究[D]. 天津：天津大学化工学院，2008.

Zhang Minge. Research on Rheological Behavior of Ultrahigh Molecular Weight HPAM Solutions and Flow Field Stirred by Double Helical Ribbon and Screw Impeller[D]. Tianjin：School of Chemical Engineering and Technology，Tianjin University，2008(in Chinese).