近光源下基于稳态空间分辨漫反射测量的光学参数反构

史振志，赵会娟，陈文亮，徐可欣

(天津大学精密仪器与光电子工程学院，天津 300072)

在体生物组织光学参数测量以及光子在生物组织中的传输问题是生物医学光子学领域的重要基础研究课题，其在光动力疗法[1]、无创血糖检测[2-3]、癌症诊断[4-5]等方面都有着潜在的应用．对漫反射光的测量可采取时间分辨、频域和稳态(或称连续光，continuous wave，CW)空间分辨测量方法．基于在体稳态测量的光学参数反构的一般原理是依据漫反射光和生物组织光学参数之间的正向模型，将空间多点测量得到的漫反射光代入反构算法得到生物组织光学参数的估计值[6-9]，因此发展快速准确的光子传输模型和反构方法显得尤为重要．

通常，辐射传输方程(radiative transfer equation，RTE)被认为是描述光子在生物组织中传输的最准确的模型，但一般来说，很难直接得到 RTE的解析解，所以研究者们发展了离散坐标法(SN)和球谐函数法(PN)等一些近似的解析解法．漫射近似(diffusion approximation，DA)作为一阶 PN 近似，是一种成功的近似模型，在生物医学领域得到了广泛的应用，然而此模型基于一些限制条件，只适用于大约化反照率( 'a)和大检测距离(source-detector separations，SDSs)的情况．随着近红外光谱在生物医学中的应用，需要新的正向模型来描述小约化反照率近光源(小检测距离)情况下的光子传输模型，例如在1,000～2,000,nm 波长的无创血糖检测的应用中，由于该波段水和皮肤组织的高吸收特性，约化反照率比较小；并且为了提高检测信噪比通常在满足探测深度的条件下采用近光源检测，所以DA不适合这样的应用．为了解决该问题，Hull和 Foster用球谐函数法推导了辐射传输方程，给出了 P3近似的格林方程，并证明了在高吸收介质近光源检测的情况下，P3近似比DA更加准确．为了修正DA和简化P3近似以适用于高吸收的介质，他们在DA的基础上结合P3近似发展了一种混合漫射近似(hybrid diffuse approximation，DAH)模型[10]．Tian 等[11]曾使用 DAH 模型来反构光学参数．另外，Klose等[12]提出了一种简化球谐函数(SPN)模型，采用有限元方法近似求解复杂的 RTE，并且证明了 SPN近似能够显著提高光子在高吸收介质小体积物体上的传输精度．

本文在大约化反照率范围(0.50～0.99)以及小检测距离(0.4～8.0,mm)下，研究了用不同的正向模型反构吸收系数(aμ)和约化散射系数('sμ)的准确性．在介绍了 6种光子传输模型(单点源和双点源模型下的 DA、DAH和 P3近似)以及反构光学参数的方法后，笔者对6种正向模型的适用范围进行数值模拟和分析，提出了一种使用不同正向模型联合反构光学参数的方法，给出了在5个不同约化反照率区间反构aμ和sμ′的最佳正向模型以及相应的反构误差．

1 方 法

1.1 正向模型

当忽略波动效应时，光子在生物组织中的传输可用RTE描述为

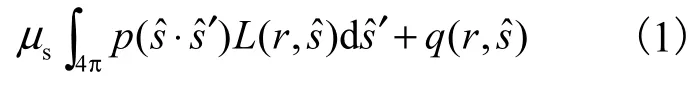
式中：L ( r,sˆ)为r处sˆ方向的平均光功率密度；q(r,sˆ)为光源分布；μs为散射系数；p(sˆ ⋅sˆ′ )为生物组织的散射相函数，描述粒子从sˆ′方向到sˆ方向散射的概率．p ( sˆ ⋅sˆ′ )通常用 Henyey-Greenstein相位函数[13]来描述为

式中：g为各向异性因子；θ为从ˆs′方向到ˆs方向的角度．

球谐函数法是用球谐函数作为基函数对 RTE进行展开，再对展开的 PN方程组进行求解，得到 PN近似．DA一般也称为P1近似，是在1阶PN近似方程的基础上进行近似简化求解得到．在无限介质以及各向同性稳态光源的情况下，DA的格林函数解可以表示为

式中：Φ为辐射通量；ρ为探测距离；effμ为有效衰减系数；D为漫射系数；sμ′为约化散射系数．

P3近似是由RTE展开的PN方程组的3阶近似解，理论上考虑了相函数的2阶矩和3阶矩，能够更加准确地描述组织的光辐射分布．因为篇幅的限制，这里不给出 P3近似具体的推导过程，具体可以参照文献[10]．

DAH的格林函数解是在DA格林函数解的基础上，分别用P3近似里面的v−和asymD 系数代替DA中的effμ和D[10]．对应方程(3)，DAH的格林函数解可表示为

其中

式中 g1、g2和 g3分别为相位函数的 1阶矩、2阶矩和 3阶矩．根据 Henyey-Greenstein相位函数，可得γ=1 + g ，δ =1 + g + g2．

在半无限介质的情况下，DA和 DAH的推导主要涉及光源的特征项以及合适的边界条件．

对于光源项，由于实际光源很复杂，将其直接用到 RTE中去求解非常困难，因此通常将光源进行简化处理．在半无限散射介质中，通常将光源看成一无限细的笔形光源，考虑该光束由z轴入射到半无限的散射介质中，有效的光源分布[14]可表示为

式中a′为约化反照率.

为了简化无限细光源的分布特征，通常采用简单的各向同性点源来代替无限细笔形光源的分布．采用一个与空气-组织界面具有相同偶极矩的光源来近似有效光源项，称之为单点源，如图 1(a)所示；而采用同时满足具有相同偶极矩和四极矩的 2种离散点源分布来近似有效光源项，称之为双点源[10-11]，如图1(b)所示．

对于单点源近似，考虑位于0z处单点源的偶极矩与式(6)表示的有效光源的偶极矩相等，可得

式(7)表示无限细光源可以用位于 z0= 1 /μt′的各向同性点源来表示，其中光源强度为约化反照率a′．

对于双点源近似，将式(7)的有效光源处理为 z01和 z02处的2个强度都为 a ′/2 的点源．考虑无限细光源和双点源的四极矩和偶极矩相等，得

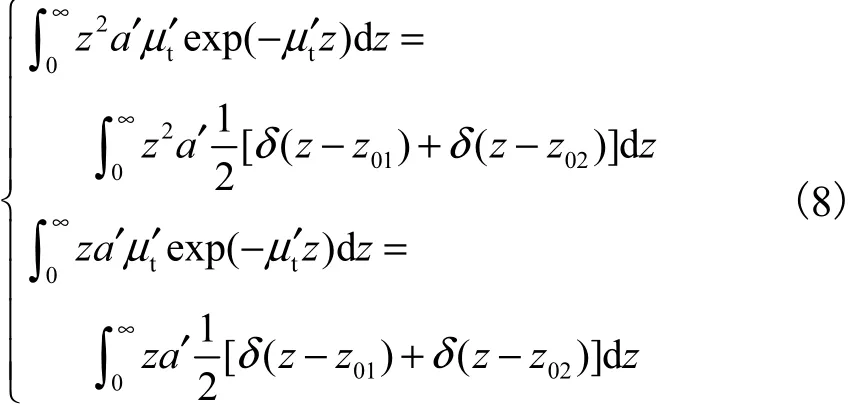
式中有效的光源深度为 z01= 2 /μt′和z02= 0 ．

对于半无限介质的边界的处理，本文采用外推边界条件来描述光在空气-组织界面的辐射通量．外推边界条件假设辐射通量在物理界面上不为零，而是在介质表面外 zb处为零(如图 1所示)[15-16]，外推边界可表示为

图1 点源近似以及外推边界条件示意Fig.1 Approximation for point sources and the extrapolated boundary condition

其中

式中effR 为有效反射系数．

为了满足外推边界条件，必须引入镜像光源，其强度与真实的光源相同，但处于外推边界的另一侧．单点源的情况下，镜像光源的位置为z=− ( 2 zb+ z0)；双点源的情况下，镜像光源的位置分别为 z1=− ( 2 zb+ z01)和 z2=− ( 2 zb+ z02)．因此，半无限介质在外推边界条件下的单点源光源项 q1(z)和双点源光源项 q2(z)可以用真实光源和镜像光源之和表示，即

根据以上的讨论，在外推边界条件下 DA和DAH的辐射通量可以表示[17]为

界面的漫反射率[15]可以表示为

式中fres()R θ为菲涅耳反射系数．

1.2 逆问题

为了研究在空间分辨漫反射测量条件下 RTE的不同解对光学参数反构的影响，用蒙特卡罗模拟产生空间分辨漫反射测量数据，而蒙特卡洛模拟中输入的吸收系数、散射系数、各向异性因子和折射系数作为光学参数的“真实值”．蒙特卡罗模拟采用了目前最广泛使用的 MCML程序[18]，用于多层半无限介质稳态光的模拟传输，程序采用了无限细的笔形光束作为光源，用 Henyey-Greenstein相位函数来计算散射角度．

反构中，分别使用单点源和两点源模型下的DA、DAH、P3近似的解通过 Levenberg-Marquadt(LM)非线性拟合对“测量值”进行拟合，反构结果与“真实值”之间的相对误差作为评价模型适应性的标准．

2 结 果

在蒙特卡罗模拟中采用了 0.1,mm的空间分辨率，最大的记录半径为 30,mm，使用了 108的光子进行运算．P3近似的推导基于 Hull等[10]的研究结果，程序代码由Finlay教授提供．

为了验证各种模型对不同约化反照率下光学参数的重构精度，在蒙特卡罗模拟中保持 µs'不变但使吸收系数从小到大变化，采用的吸收系数为 µa＝0.01,mm-1、0.1,mm-1、0.5,mm-1、1.0,mm-1，其他光学参数为sμ′＝1,mm-1，g＝0.9，n＝1.4．蒙特卡罗模拟中半无限介质的空间分辨探测如图 2(a)所示，探测的范围 ρ为 ρmin～8.0,mm，间隔 0.1,mm．ρmin代表在进行空间分辨测量时所采用的最小探测距离，ρmin的范围为 0.4～4.0,mm，间隔是 0.1,mm．对同一组光学参数在一系列 ρ下蒙特卡罗模拟得出的“测量值”与使用单点源和两点源模型下的DA、DAH和P3近似的解进行非线性拟合，得到光学参数的重构值，光学参数的反构原理如图2(b)所示．

图 2 蒙特卡罗模拟中半无限介质的空间分辨探测及组织光学参数反构示意Fig.2 Scheme of steady-state spatially resolved diffuse reflectance of Monte Carlo simulation under semiinfinite medium and the derivation of optical properties

图 3～图 6给出了使用上述 6种模型在不同 a '下反构μa和μs′的结果．图3～图6的结果表明：光学参数的准确计算取决于正向模型的选择，并且不同的ρmin影响μa和μs′的反构结果．当a'= 0 .99时(如图 3所示)，反构μa最佳的正向模型为双点源的DA和DAH，在最小探测距离 ρmin为 0.6～4.0,mm 的情况下，反构误差＜10%；而反构μs′最佳的正向模型为单点源的 DA 和 DAH，在 ρmin为 0.4～4.0,mm 的情况下，反构误差在0.6%～7.0%之间．当 a '= 0 .91时(见图4)，反构μa和μs′最佳的正向模型都为单点源的DAH，在 ρmin为0.7～4,mm的情况下，μa的反构误差＜10%；在 ρmin为1.7～4.0,mm的情况下，μs′的反构误差＜10%．当 a'= 0 .67时(图 5)，双点源的 DAH模型优于其他的模型，在ρmin为0.4～2.6,mm的情况下，μa的反构误差＜5%；在ρmin为0.5～2.6,mm的情况下，μs′的反构误差＜5%．当a'=0.5时(图6)，单点源DA适合反构μa，在 ρmin为0.7～2.4,mm的情况下，反构误差＜6%；对于μs′，这些模型的反构准确度都不高，双点源的 DAH 模型的误差最小，在 ρmin为0.4～1.2,mm 的情况下，反构误差仅为 20%左右．但是，无论是单点源的 P3近似还是双点源的 P3近似在光学参数的计算中都没有得到好的结果．这是因为虽然 P3是高阶近似，并且已经证明了在高吸收介质近光源检测的情况下P3近似比DA更加准确，但P3近似也不是任何时候都比DA更加准确．

图3 a′=0.99时吸收系数和约化散射系数的反构结果Fig.3 Derived absorption coefficient and reduced scattering coefficient at a′=0.99

图4 a′=0.91时吸收系数和约化散射系数的反构结果Fig.4 Derived absorption coefficient and reduced scattering coefficient at a′=0.91

图5 a′=0.67时吸收系数和约化散射系数的反构结果Fig.5 Derived absorption coefficient and reduced scattering coefficient at a′=0.67

图6 a′=0.50时吸收系数和约化散射系数的反构结果Fig.6 Derived absorption coefficient and reduced scattering coefficient at a′=0.50

为了更深入地研究以上模型的适用性，将 a '为0.50～0.99的区间进一步细分，使用 19组不同的吸收 系 数 (μa＝ 0.01,mm-1，0.02,mm-1，0.03,mm-1，0.04,mm-1，0.05,mm-1，0.06,mm-1，0.07,mm-1，0.08,mm-1，0.09,mm-1，0.10,mm-1，0.20,mm-1，0.30,mm-1，0.40,mm-1，0.50,mm-1，0.60,mm-1，0.70,mm-1，0.80,mm-1，0.90,mm-1，1.00,mm-1)，设μs′=1,mm-1，g＝0.9，n＝1.4，形成了 5 个约化反照率的区间 ，即0.96 ≤ a '≤ 0 .99的 “ 样 品 ” 有 4个(μa＝0.01,mm-1，0.02,mm-1，0.03,mm-1，0.04,mm-1)，0.91≤a'＜0.96的样品有7个(μa＝0.04,mm-1，0.05,mm-1，0.06,mm-1，0.07,mm-1，0.08,mm-1，0.09,mm-1，0.10,mm-1)，0.71 ≤ a '＜0 . 91的样品有4个(μa＝0.10,mm-1，0.20,mm-1，0.30,mm-1，0.40,mm-1)，0.62≤a'＜0.71的样品有3个(μa＝0.40,mm-1，0.50,mm-1，0.60,mm-1)，0.5≤a'＜0.62的样品有5个(μa＝0.60,mm-1，0.70,mm-1，0.80,mm-1，0.90,mm-1，1.00,mm-1)．

对各个模型反构结果进行比较，得到了在不同约化反照率范围条件下最佳的正向模型，如表1所示．

表1 在不同约化反照率情况下反构吸收系数和约化散射系数的最佳模型Tab.1 The best model to derive absorption coefficient and reduced scattering coefficient together at different ranges of reduced albedo

0.96 ≤ a'≤ 0.99下反构μa的最佳正向模型为双点源的混合漫射近似，反构μs′的最佳正向模型为单点源的混合漫射近似；在0.91≤a'＜0.96下，反构μa和μs′的正向模型同为单点源的混合漫射近似；在0.71≤a'＜0.91下，反构μa的最佳正向模型为单点源的漫射近似，反构μs′的最佳正向模型为双点源的漫射近似；在0.62≤a'＜0.71下，反构μa和μs′的正向模型同为双点源的混合漫射近似；在0.50'0.62a≤＜下，反构aμ的最佳正向模型为单点源的漫射近似，反构sμ′的最佳正向模型为双点源的混合漫射近似．

根据以上结果，提出一种计算光学参数的联合反构方法，和以往反构aμ和sμ′时使用同一种正向模型不同的是，联合反构算法不仅在不同约化反照率时使用不同的正向模型，而且反构aμ和sμ′时也使用不同的正向模型．例如当μa＝0.7,mm-1，sμ′＝1,mm-1时，如果只是使用传统的单一的正向模型(如单点源的漫射近似)，吸收系数的反构误差为 0.14%，约化散射系数的反构误差仅为 49.1%；使用了联合反构算法，吸收系数的反构误差因为同为单点源漫射近似所以同为 0.14%，而约化散射系数的反构误差为 10.4%，有了很大的提高．

在光学参数的反构问题中，最小二乘问题是求方程的平方和的最小化，而正向问题的准确性是反构问题的关键．从图 7可以看出，各个理论模型的漫反射率与模拟结果的偏差各不相同，尤其在本文所选择的最小检测距离的范围(0.4,mm≤ρmin≤4.0,mm)下，变化的浮动较大，而随着光源探测的距离减小，漫反射率的值也越大．所以选择不同的最小检测距离 ρmin，使得方程的平方和的值变化浮动增大，从而在最小化的拟合过程中，使得反构结果的误差增大，从而表明了合理选择ρmin的重要性．为了将这一结论对实际的光学参数计算具有指导意义，研究了最小探测距离ρmin的选取范围．使用表 1给出的最佳正向模型，表2给出了对19组光学参数进行反构时最佳的ρmin范围，并给出了相应的反构误差范围．结果表明，在光学参数计算的过程中，选择合适的最小探测距离 ρmin对提高光学参数的反构精度有很大的帮助．

图7 理论模型与模拟结果的漫反射率的偏差Fig.7 Variety of diffuse reflectance of theoretical models and simulation results

表2 19组光学参数条件下最优的最小探测距离ρmin范围以及相应的反构误差Tab.2 ρmin and the corresponding derivation error range in case of 19 kinds of e derived absorption coefficient and reduced scattering coefficient

3 结 语

研究了在近光源(光源检测器范围0.4～8.0,mm)和大的约化反照率范围(0.50～0.99)的情况下吸收系数和约化散射系数的反构问题，使用了6种光学传输模型对光学参数的计算进行了讨论．为了细致地研究各个正向模型的适用性，在约化反照率范围为0.50～0.99的情况下，选取了 19组光学参数通过对模拟数据的拟合来进行光学参数的计算．由于篇幅的原因，本文没有给出所有的计算结果，只给出了在5个约化反照率范围用于反构aμ和sμ′的最佳模型．从结果中可以看出光学参数的准确计算取决于正向模型的正确选择，并且aμ和sμ′的计算都有各自的适用模型，在此 'a范围内未必使用高阶的PN近似就能取得好的结果，而DA和DAH适用于这些 'a范围内的aμ和sμ′重建．另外还研究了最小探测距离ρmin的选取范围并给出了相应的反构误差，得出不同的ρmin值的选择影响aμ和sμ′的反构精度．

根据计算和分析，在近光源(光源检测器范围0.4～8.0,mm)和大的约化反照率范围(0.50～0.99)的情况下，提出了计算光学参数的联合反构方法，即在不同的约化反照率下，使用不同的正向模型来分别反构吸收系数和约化散射系数，如表 1所示．如果在重构之前或重构过程中已知 'a的范围，则可根据 'a选择最佳的正向模型，从而达到降低重构误差的目的．但在实际的光学参数测量过程中，光学参数的值是未知的，所以无法判断 'a的值．故将联合反构算法应用于实际之前，需要构建一个正确选择正向模型的预判体系．本文主要介绍光学参数联合反构的方法，而这个正确选择正向模型的预判体系会在结合具体实际应用的过程中进一步去进行研究．

本文只讨论了在sμ′固定(同为1,mm-1)的情况下各个正向模型在不同 'a下的适用性，未来会研究由不同的sμ′所导致的不同'a范围内正向模型的适用性，从而得到更加完善的光学参数联合反构方法．

［1］ Wilson B C，Patterson M S. The physics，biophysics and technology of photodynamic therapy[J]. Physics in Medicine and Biology，2008，53(9)：R61-R109.

［2］ Bykov A V，Kirillin M Y，Priezzhev A V，et al. Simulations of a spatially resolved reflectometry signal from a highly scattering three-layer medium applied to the problem of glucose sensing in human skin[J]. Quantum Electronics，2006，36(12)：1125-1130.

［3］ Yang Yue，Chen Wenliang，Shi Zhenzhi，et al. The reference point of floating-reference method for blood glucose sensing[J]. Chinese Optical Letter，2010，8(4)：421-424.

［4］ Zhu C，Palmer G M，Breslin T M，et al. Use of a multiseparation fiber optic probe for the optical diagnosis of breast cancer[J]. Journal of Biomedical Optics，2005，10(2)：024032.

［5］ Pavlova I，Weber C R，Schwarz R A，et al. Monte Carlo model to describe depth selective fluorescence spectra of epithelial tissue：Applications for diagnosis of oral precancer[J]. Journal of Biomedical Optics，2008，13(6)：064012.

［6］ Doornbos R M P，Lang R，Aalders M C，et al. The determination of in vivo human tissue optical properties and absolute chromophore concentrations using spatially resolved steady-state diffuse reflectance spectroscopy[J].Physics in Medicine and Biology，1999，44(4)：967-981.

［7］ Arifler D. Sensitivity of spatially resolved reflectance signals to coincident variations in tissue optical properties[J]. Applied Optics，2010，49(20)：4310-4320.

［8］ Cen H，Lu R. Quantification of the optical properties of two-layer turbid materials using a hyperspectral imagingbased spatially-resolved technique[J]. Applied Optics，2009，48(29)：5612-5623.

［9］ Pilz M，Honold S，Kienle A. Determination of the optical properties of turbid media by measurements of the spatially resolved reflectance considering the pointspread function of the camera system[J]. Journal of Biomedical Optics，2008，13(5)：054047.

［10］ Hull E L，Foster T H. Steady-state reflectance spectroscopy in the P3 approximation[J]. Journal of the Optical Society of America A，2001，18(3)：584-599.

［11］ Tian Huijuan，Liu Ying，Wang Lijun，et al. Hybrid diffusion approximation in highly absorbing media and its effects of source approximation[J]. Chinese Optical Letter，2009，7(6)：515-518.

［12］ Klose A D，Larsen E W. Light transport in biological tissue based on the simplified spherical harmonics equations[J]. Journal of Computational Physics，2006，220：441-470.

［13］ Henyey L G，Freyer J L. Diffuse radiation in the galaxy[J]. The Astrophysical Journal，1941，93：70-83.

［14］ Farrell T J，Patterson M S，Wilson B C. A diffusion theory model of spatially resolved，steady-state diffuse reflectance for the noninvasive determination of tissue optical properties in vivo[J]. Medical Physics，1992，19(4)：879-888.

［15］ Kienle A，Patterson M S. Improved solutions of the steady-state and the time-resolved diffusion equations for reflectance from a semi-infinite turbid medium[J].Journal of the Optical Society of America A，1997，14(1)：246-254.

［16］ Haskell R C，Svaasand L O，Tsay T，et al. Boundary conditions for the diffusion equation in radiative transfer[J]. Journal of the Optical Society of America A，1994，11(10)：2727-2741.

［17］ Tualle J M，Prat J，Tinet E，et al. Real-space Green's function calculation for the solution of the diffusion equation in stratified turbid media[J]. Journal of the Optical Society of America A，2000，17(11)：2046-2055.

［18］ Wang Lihong，Jacques S L，Zheng Liqiong. MCMLMonte Carlo modeling of light transport in multi-layered tissue[J]. Computer Methods and Programs in Biomedicine，1995，47(2)：131-146.